Thought it only used recursion, but it actually also used backtracking
# 257. Binary Tree Paths
LeetCode Problem Link (opens new window)
Given a binary tree, return all root-to-leaf paths.
Note: A leaf node is one that does not have any child nodes.
Example:

# Thought Process
This problem requires finding paths from the root node to leaf nodes, so preorder traversal is needed, as it ensures that parent nodes point to child nodes to find the corresponding paths.
This problem introduces backtracking as well, because while recording paths, one needs to backtrack to retreat a path and proceed to another path.
The process of preorder traversal and backtracking is illustrated in the graphic:
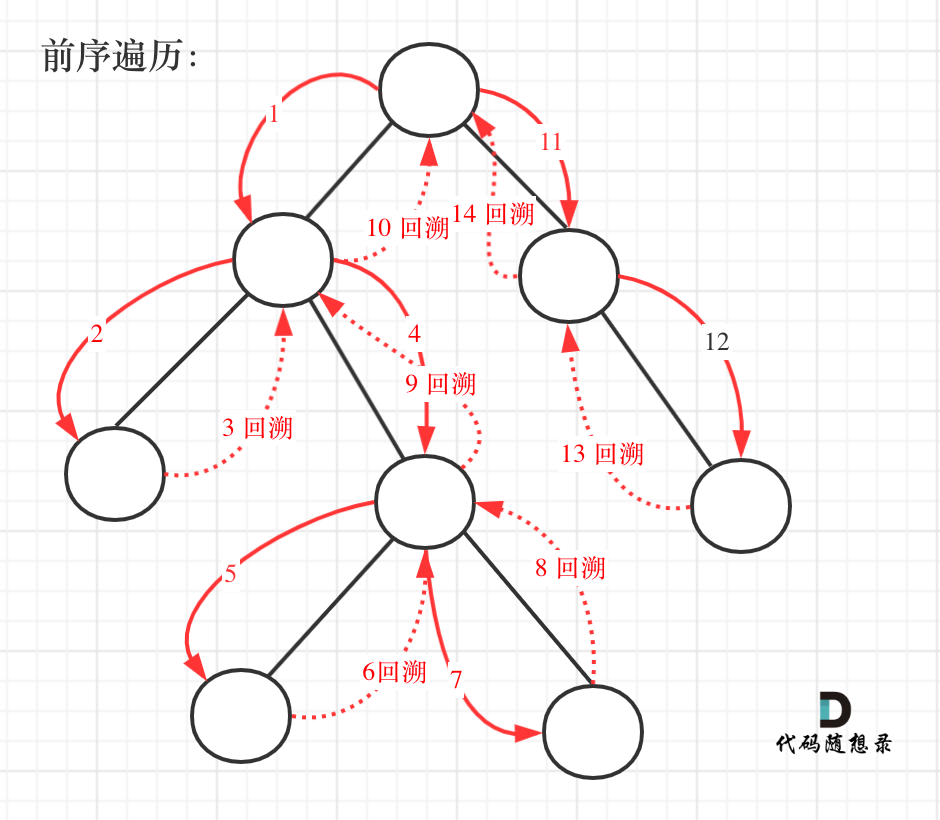
We will first employ the recursive method for preorder traversal. It is crucial to understand that recursion and backtracking are essentially inseparable; this problem requires backtracking.
# Recursion
- Recursive Function Parameters and Return Value
We need to pass the root node, a vector to record each path, and a vector to store the result set. Here, the recursion does not require a return value. The code appears as follows:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)
- Determine the Recursion Termination Condition
When writing recursion, it is customary to write something like this:
if (cur == NULL) {
Termination logic
}
2
3
However, this problem’s termination condition is more complex. Once we reach a leaf node, we need to stop processing logic and record the path in result.
When do we consider a node as a leaf node? It is when both the left and right children of a non-null cur are null that we have found a leaf node.
So, the termination condition for this problem is as follows:
if (cur->left == NULL && cur->right == NULL) {
Termination logic
}
2
3
Why didn't we check if cur is null? The subsequent logic will ensure that null nodes do not enter the loop.
Let's further explore the termination logic.
Here, we use a vector<int> structure path to record the path, so the vector needs to be converted into a string format and the string needs to be placed in result.
Why choose vector<int> structure for the path? Because during the single-layer recursive logic processing, backtracking is necessary, and using vector facilitates backtracking.
Some might argue that in some solutions, backtracking logic isn’t visible.
In reality, backtracking is present; it's just hidden within the function call parameter assignment, which is discussed further below.
We're using a vector<int> structure for the path container, and the termination logic is as follows:
if (cur->left == NULL && cur->right == NULL) { // Encountering a leaf node
string sPath;
for (int i = 0; i < path.size() - 1; i++) { // Convert recorded path in vector to string format
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]); // Record the last node (leaf node)
result.push_back(sPath); // Collect a path
return;
}
2
3
4
5
6
7
8
9
10
- Determine the Single-Layer Recursive Logic
Since it's preorder traversal, we process the middle node first, which needs to be recorded in path.
path.push_back(cur->val);
Then comes the recursion and backtracking part. We mentioned that we do not check if cur is null, so before recursion, a check for null is needed for the nodes to be recursively called:
if (cur->left) {
traversal(cur->left, path, result);
}
if (cur->right) {
traversal(cur->right, path, result);
}
2
3
4
5
6
After recursion, backtracking is necessary as well; otherwise, path would continuously add nodes without removing them, preventing new nodes from being added.
How should backtracking be done? Some might type it as follows:
if (cur->left) {
traversal(cur->left, path, result);
}
if (cur->right) {
traversal(cur->right, path, result);
}
path.pop_back();
2
3
4
5
6
7
This backtracking has significant issues. We know that backtracking and recursion are one-to-one correspondences; with each recursion, a corresponding backtrack is required. Writing it like this separates recursion from backtracking, one is inside the braces, and the other is outside.
Backtracking should always be with recursion, like being together in the same block!
The code should therefore be written like this:
if (cur->left) {
traversal(cur->left, path, result);
path.pop_back(); // Backtrack
}
if (cur->right) {
traversal(cur->right, path, result);
path.pop_back(); // Backtrack
}
2
3
4
5
6
7
8
Below is the overall code for this problem:
// Version One
class Solution {
private:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
path.push_back(cur->val); // Process middle node, add to path
if (cur->left == NULL && cur->right == NULL) { // Found a leaf node
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath); // Collect a path
return;
}
if (cur->left) { // Process left
traversal(cur->left, path, result);
path.pop_back(); // Backtrack
}
if (cur->right) { // Process right
traversal(cur->right, path, result);
path.pop_back(); // Backtrack
}
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
vector<int> path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
The above C++ code clearly demonstrates backtracking.
The code can be further simplified as follows:
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // Process middle node
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) traversal(cur->left, path + "->", result); // Process left
if (cur->right) traversal(cur->right, path + "->", result); // Process right
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
The above code hides many important details.
Notably, in defining the function as void traversal(TreeNode* cur, string path, vector<string>& result), string path is defined so that it's copied each time, rather than using a reference, thus achieving a backtracking effect. (This involves C++ syntax knowledge)
Some may argue that there's seemingly no backtracking logic present. It is, however, hidden in traversal(cur->left, path + "->", result); through the use of path + "->". Once the function call completes, path remains without "->", which is the essence of backtracking.
To further illustrate the backtracking hidden in the simplified code, you may experiment by changing this snippet:
if (cur->left) traversal(cur->left, path + "->", result); // Backtracking is hidden here
to
path += "->";
traversal(cur->left, path, result); // Process left
2
Thus:
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // Process left
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // Process right
}
2
3
4
5
6
7
8
Currently, without backtracking, the code would not succeed.
To remediate without altering backtracking, adjust the above code by incorporating backtracking so it can pass:
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // Left
path.pop_back(); // Backtrack '>'
path.pop_back(); // Backtrack '-'
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // Right
path.pop_back(); // Backtrack '>'
path.pop_back(); // Backtrack '-'
}
2
3
4
5
6
7
8
9
10
11
12
The overall code for this can be:
// Version Two
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // Process middle node
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // Left
path.pop_back(); // Backtrack '>'
path.pop_back(); // Backtrack '-'
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // Right
path.pop_back(); // Backtrack '>'
path.pop_back(); // Backtrack '-'
}
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Combining these points, the second version of the recursive code, while simplified, conceals many critical details. The first version showcases all logic involved in a clearer, more transparent manner.
# Exploration
Here, we delve into the logic underlying this solution along with more detailed nuances. If you aren't a C++ user, you may skip this to avoid confusion.
For C++ users, it is advisable to tackle this problem at least twice independently before reading the following elaboration, also to prevent unnecessary confusion.
In the second version of the code, only the parts -> were backtracked (invoking pop_back twice to backtrack > and -). One may wonder why path += to_string(cur->val); wasn't backtracked. How can a continuous path accumulate nodes without backtracking?
The crux lies in the parameter, defined as string path, without reference &. Thus, within this layer, path is modified by adding the node's value, but after this recursion ends, the path value remains unaltered from the preceding layer (akin to backtracking). As depicted:
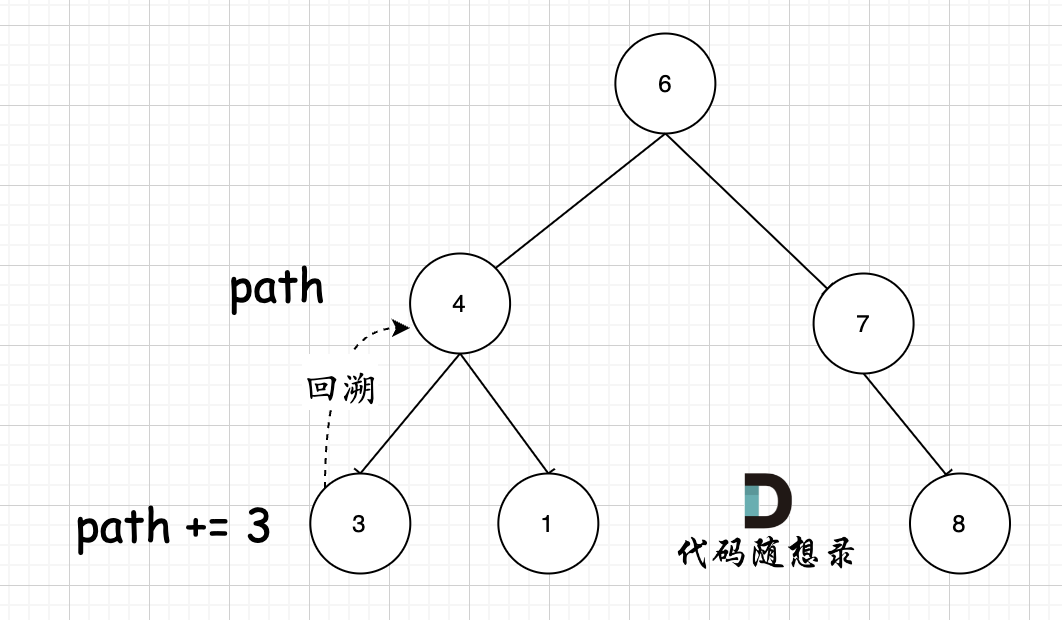
In node 4’s path, on reaching node 3, path + 3 occurs; however, post node 3's recursion, path returns to node 4 (the backtracking process), where 3 is not included.
Thus, function parameters without reference possess content copying, rather than address copying, manifested here. (Involves C++ referential knowledge)
In the first version of the code, I precisely use reference in the function parameter, vector<int>& path in this case, which copies addresses. So, if one layer has path.push_back(cur->val);, a corresponding path.pop_back() is mandatory.
Perhaps one might wonder, why not define string& path in the function parameter? The issue arises in that path += to_string(cur->val); continuously adds digits, whether they are single, double, or triple-digit numbers. To achieve accurate backtracking, multiple pop_back() calls would become overly verbose.
Hence, in version one, using the vector type path makes it convenient to demonstrate the code's backtracking process. Regardless of whether the path accumulates multiple digits, backtracking is consistent by popping back an int from the vector, efficiently reducing redundancy compared to dealing with strings.
# Iterative Method
For the non-recursive approach, we can employ iteration to mimic path traversal. Those unfamiliar with the iterative traversal can refer to the articles Binary Tree Iterative Traversal (opens new window) and Unified Iterative Traversal of Binary Tree (opens new window).
This method involves using a stack to simulate recursive traversal and another stack to store corresponding paths.
Below is the C++ implementation:
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
stack<TreeNode*> treeSt; // Saves traversed tree nodes
stack<string> pathSt; // Saves the traversed path nodes
vector<string> result; // Final path collection
if (root == NULL) return result;
treeSt.push(root);
pathSt.push(to_string(root->val));
while (!treeSt.empty()) {
TreeNode* node = treeSt.top(); treeSt.pop(); // Get node, mid
string path = pathSt.top(); pathSt.pop(); // Get path corresponding to node
if (node->left == NULL && node->right == NULL) { // Leaf node encountered
result.push_back(path);
}
if (node->right) { // right
treeSt.push(node->right);
pathSt.push(path + "->" + to_string(node->right->val));
}
if (node->left) { // left
treeSt.push(node->left);
pathSt.push(path + "->" + to_string(node->left->val));
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Of course, those using Java can directly define a stack as Stack<Object> stack = new Stack<>(); instead of defining two separate stacks, storing everything in one stack.
# Conclusion
This article introduces backtracking concepts; many may have solved the problem without recognizing the employment of backtracking, where recursion and backtracking are inseparable.
In the first version, every logical progression and corresponding backtrack is explicitly demonstrated, allowing a comprehensive understanding.
The second version, although simplified, conceals setup details within the finer aspects of its code.
Lastly, an iterative approach is provided. Those invested should aim to implement the iterative method after understanding recursion and backtracking thoroughly.
# Other Language Versions
# Java:
// Solution One
// Method One
class Solution {
/**
* Recursive Method
*/
public List<String> binaryTreePaths(TreeNode root) {
List<String> res = new ArrayList<>(); // Store final result
if (root == null) {
return res;
}
List<Integer> paths = new ArrayList<>(); // As path in result
traversal(root, paths, res);
return res;
}
private void traversal(TreeNode root, List<Integer> paths, List<String> res) {
paths.add(root.val); // Preorder traversal, process middle node
// Encounter leaf node
if (root.left == null && root.right == null) {
// Output
StringBuilder sb = new StringBuilder(); // StringBuilder is faster for string concatenation
for (int i = 0; i < paths.size() - 1; i++) {
sb.append(paths.get(i)).append("->");
}
sb.append(paths.get(paths.size() - 1)); // Record last node
res.add(sb.toString()); // Collect a path
return;
}
// Recursion and backtrack occur simultaneously, so within same brace
if (root.left != null) { // left
traversal(root.left, paths, res);
paths.remove(paths.size() - 1); // Backtrack
}
if (root.right != null) { // right
traversal(root.right, paths, res);
paths.remove(paths.size() - 1); // Backtrack
}
}
}
// Method Two
class Solution {
List<String> result = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
deal(root, "");
return result;
}
public void deal(TreeNode node, String s) {
if (node == null)
return;
if (node.left == null && node.right == null) {
result.add(new StringBuilder(s).append(node.val).toString());
return;
}
String tmp = new StringBuilder(s).append(node.val).append("->").toString();
deal(node.left, tmp);
deal(node.right, tmp);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
// Solution Two
class Solution {
/**
* Iterative Method
*/
public List<String> binaryTreePaths(TreeNode root) {
List<String> result = new ArrayList<>();
if (root == null)
return result;
Stack<Object> stack = new Stack<>();
// Both node and path enter the stack
stack.push(root);
stack.push(root.val + "");
while (!stack.isEmpty()) {
// Both node and path leave the stack
String path = (String) stack.pop();
TreeNode node = (TreeNode) stack.pop();
// If leaf node found
if (node.left == null && node.right == null) {
result.add(path);
}
// Right child node is not null
if (node.right != null) {
stack.push(node.right);
stack.push(path + "->" + node.right.val);
}
// Left child node is not null
if (node.left != null) {
stack.push(node.left);
stack.push(path + "->" + node.left.val);
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# Go:
Recursive Method:
func binaryTreePaths(root *TreeNode) []string {
res := make([]string, 0)
var travel func(node *TreeNode, s string)
travel = func(node *TreeNode, s string) {
if node.Left == nil && node.Right == nil {
v := s + strconv.Itoa(node.Val)
res = append(res, v)
return
}
s = s + strconv.Itoa(node.Val) + "->"
if node.Left != nil {
travel(node.Left, s)
}
if node.Right != nil {
travel(node.Right, s)
}
}
travel(root, "")
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Iterative Method:
func binaryTreePaths(root *TreeNode) []string {
stack := []*TreeNode{}
paths := make([]string, 0)
res := make([]string, 0)
if root != nil {
stack = append(stack, root)
paths = append(paths, "")
}
for len(stack) > 0 {
l := len(stack)
node := stack[l-1]
path := paths[l-1]
stack = stack[:l-1]
paths = paths[:l-1]
if node.Left == nil && node.Right == nil {
res = append(res, path+strconv.Itoa(node.Val))
continue
}
if node.Right != nil {
stack = append(stack, node.Right)
paths = append(paths, path+strconv.Itoa(node.Val)+"->")
}
if node.Left != nil {
stack = append(stack, node.Left)
paths = append(paths, path+strconv.Itoa(node.Val)+"->")
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
