Initially, I planned to discuss the problem of finding the lowest common ancestor in both binary trees and binary search trees together. However, I realized the content became too lengthy, so I will first address the problem in binary trees.
# 236. Lowest Common Ancestor of a Binary Tree
LeetCode Problem Link (opens new window)
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
The definition of the lowest common ancestor on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
For example, the given binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]
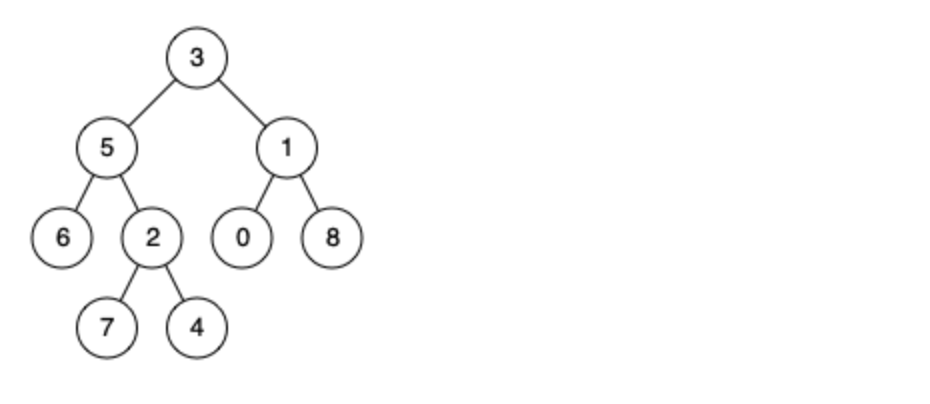
Example 1: Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 Output: 3 Explanation: The lowest common ancestor of nodes 5 and 1 is node 3.
Example 2: Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 Output: 5 Explanation: The lowest common ancestor of nodes 5 and 4 is 5, as a node can be a descendant of itself according to the definition.
Note:
- All node values are unique.
pandqare different and both values will exist in the given binary tree.
# Approach
When facing this problem, the first thought is to perform a bottom-up search to find the common ancestor.
How can we search a binary tree from bottom to top?
Backtracking is the solution, where the process of backtracking in binary trees inherently occurs from bottom to top.
Postorder traversal (left-right-root) naturally carries out this backtracking process, as we can handle the logic at the node based on the return values from the left and right subtrees.
Next, how do we determine whether a node is the common ancestor of nodes q and p?
The most straightforward situation is: when one of the nodes appears in the left subtree, and the other appears in the right subtree, or vice versa, that node is the lowest common ancestor of p and q. This is Case 1:
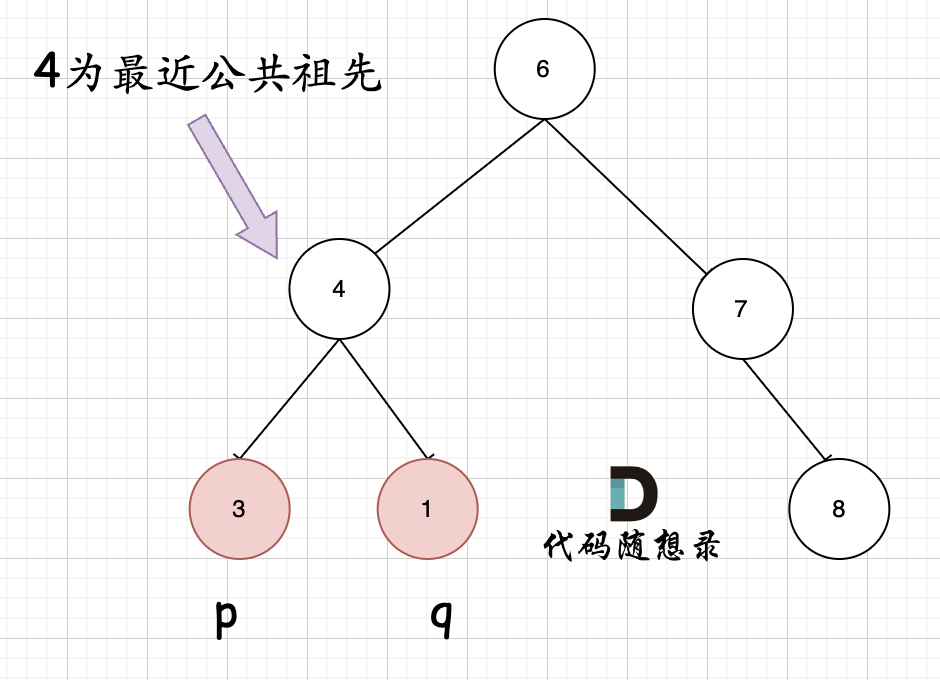
The logic is that if during recursive traversal you encounter q, you return q, and if p is encountered, you return p. If the return values of both the left and right subtrees are non-null, then the current node must be the lowest common ancestor of q and p.
Some might worry about whether it's possible for the left subtree to return q and the right subtree to return q as well, thus failing to find the lowest common ancestor of q and p.
Such worries are unfounded given that the problem stipulates: The binary tree nodes have unique values, and q and p both exist in the tree.
Another frequently overlooked case is when the node itself p(q) has a descendant q(p). This is Case 2:
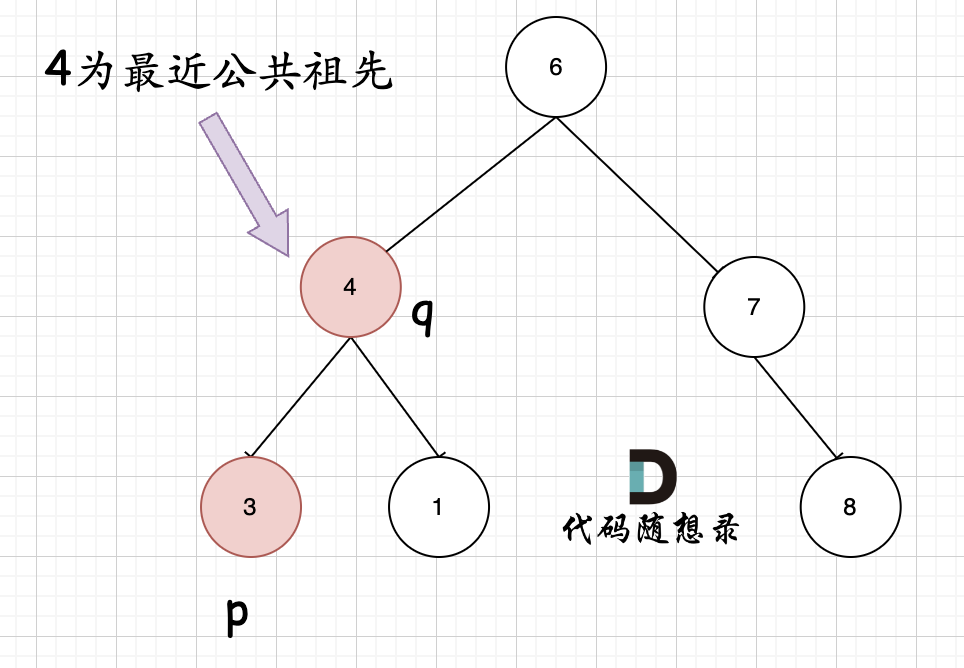
In fact, the procedure for realizing Case 1 also implicitly includes Case 2.
Because when you return a node q or p, it naturally handles the situation where either q or p is the common ancestor itself.
Let’s go through the recursive process:
- Determine the return value and parameters of the recursive function
The recursive function needs a return value to inform us whether node q or node p has been found, so a boolean return type would suffice.
However, we also need to return the nearest common node. Leveraging the problem where the return type is TreeNode*, we return q or p when they are found. A non-null return value indicates that q or p has been located.
Here's the code example:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
- Define the termination condition
If we encounter a null node, the tree is exhausted, and we return null.
Additionally, if root == q, or root == p, it suggests we have located q or p, thus returning the node found. This return value will be utilized later when handling the root node logic.
The code looks like this:
if (root == q || root == p || root == NULL) return root;
- Define the single-layer recursive logic
It’s important to notice that the function has a return value due to the need to use the recursive function's return value to create logical judgments during backtracking. However, we still need to traverse all nodes of the tree.
In the article titled 0112.Path Sum (opens new window), it was mentioned that when and why a recursive function needs a return value versus when it doesn't.
When a recursive function has a return value, how do we differentiate between searching a single path versus searching the entire tree?
Single path search:
if (recursive_function(root->left)) return ;
if (recursive_function(root->right)) return ;
2
3
Whole tree search:
left = recursive_function(root->left); // Left
right = recursive_function(root->right); // Right
Logic handling between left and right; // Root
2
3
Do you see the difference?
In a recursive function with a return value: if you only want to search a single path, immediately return when the recursive function's return value is non-null. For searching the entire tree, directly assign values to left and right for further logical processing at the root node (during backtracking).
Why search the entire tree? Intuitively, once the lowest common ancestor is found, it could be returned instantly.
For instance:
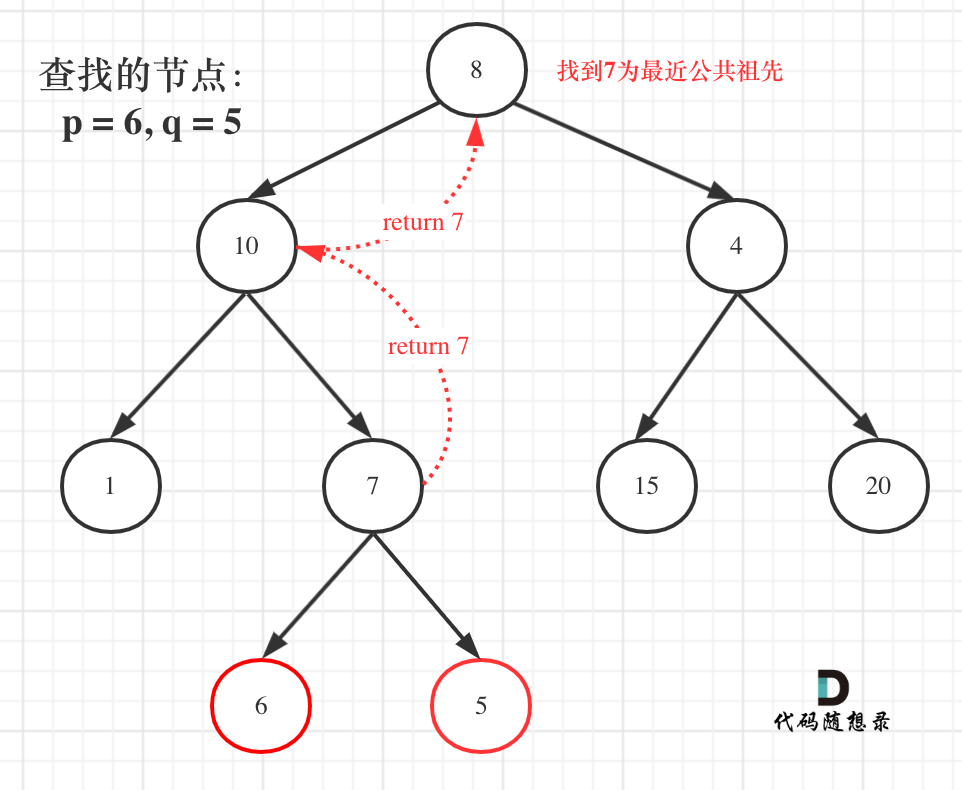
In the diagram, return node 7 directly.
However, the right subtree of the root also needs to be traversed (even if the target node is already found), covering nodes such as 4, 15, and 20.
Because in the postorder traversal code, if you want to use left and right for logical processing, you cannot return immediately; logical processing must be done after left and right are processed.
The relevant code is:
left = recursive_function(root->left); // Left
right = recursive_function(root->right); // Right
Logic handling between left and right; // Root
2
3
So you need to know that we have to traverse the entire tree. Understanding this will give you deeper insight into this problem.
By using left and right to capture the return values of the left and right subtrees:
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
2
3
If both left and right are non-null, it implies that root is the nearest common node.
If left is null and right is non-null, return right, indicating that the target node was found through the right. Conversely, do the opposite.
Some might struggle to grasp why right is returned when left is null and cannot see how the target node returns through right.
Consider the diagram:
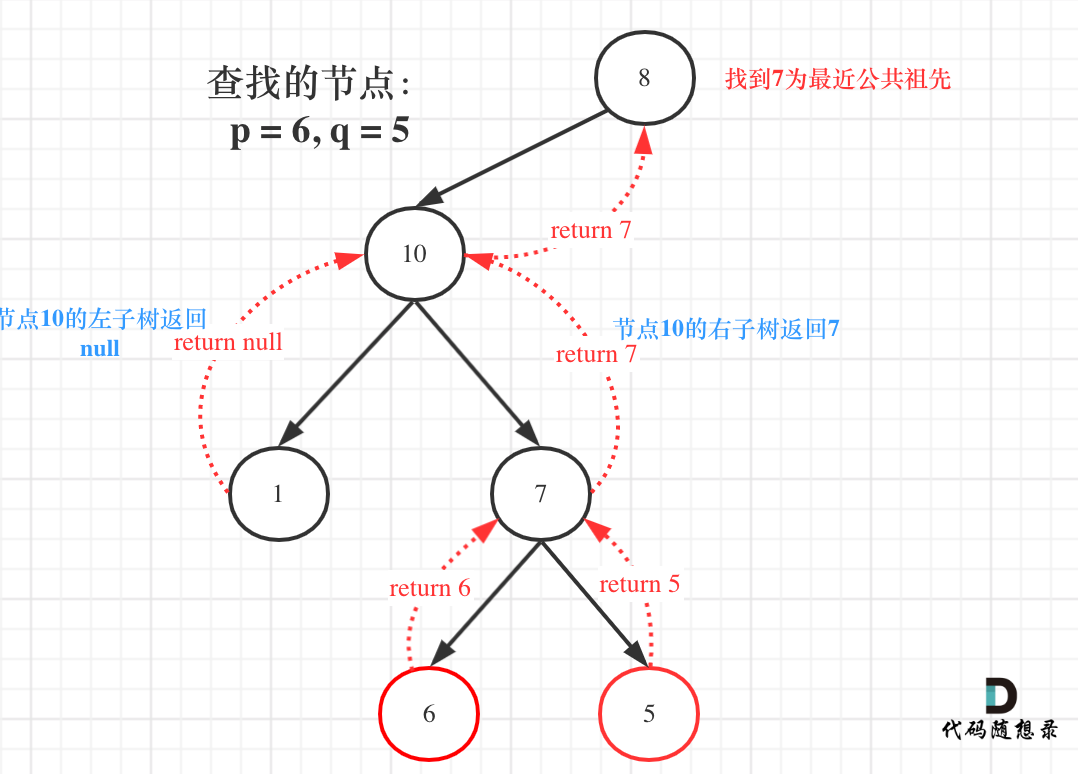
In this case, node 10's left subtree returns null, and the right subtree returns target value 7, so the logic at node 10 is to return the right subtree's return value (the nearest common ancestor 7) upwards!
Understanding this point is essential, as many who have attempted this problem may not know how the result is propagated upwards from the bottom layer to the head node.
If both left and right are null, return either left or right; both can return null.
Here's the code:
if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else { // (left == NULL && right == NULL)
return NULL;
}
2
3
4
5
6
The full process of finding the nearest common ancestor is illustrated below:
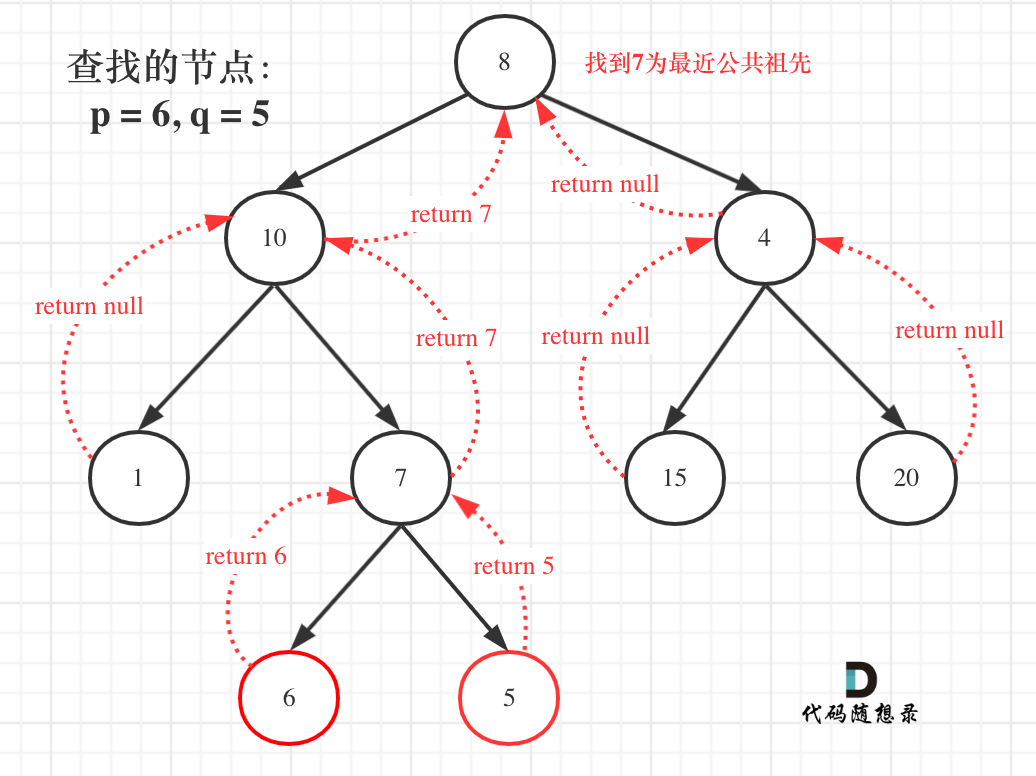
From the diagram, you can see how we backtrack to traverse the entire binary tree and return the result to the head node!
Complete code:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == q || root == p || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) return root;
if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else { // (left == NULL && right == NULL)
return NULL;
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Slightly refined, the code is as follows:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == q || root == p || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) return root;
if (left == NULL) return right;
return left;
}
};
2
3
4
5
6
7
8
9
10
11
# Conclusion
Many who have solved this problem might not fully understand the backtracking process nor how the result is passed layer by layer upwards.
My three recommendations are as follows:
Finding the lowest common ancestor involves traversing from bottom to top; thus, the binary tree can only be traversed from bottom to top via postorder traversal (i.e., backtracking).
In the backtracking process, the entire binary tree must be traversed, even if the result has been found, because we need the recursive function’s return value (i.e., left and right) for logical decisions.
Understand why when the return value left is null yet right is non-null, you should return right, and how this return of right transfers the result upwards.
It's appropriate not to provide iterative solutions for this problem, as iteration is unsuitable for simulating the backtracking process. Understanding the recursive solution suffices.
# Other Language Versions
# Java
Recursion
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) { // Recursive termination condition
return root;
}
// Postorder traversal
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null && right == null) { // If neither p nor q is found
return null;
}else if(left == null && right != null) { // If one of the nodes is found
return right;
}else if(left != null && right == null) { // If one of the nodes is found
return left;
}else { // If both nodes are found
return root;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Iteration
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
int max = Integer.MAX_VALUE;
Stack<TreeNode> st = new Stack<>();
TreeNode cur = root, pre = null;
while (cur != null || !st.isEmpty()) {
while (cur != null) {
st.push(cur);
cur = cur.left;
}
cur = st.pop();
if (cur.right == null || cur.right == pre) {
// If p/q is the root/left or root/right, return root
if (cur == p || cur == q) {
if ((cur.left != null && cur.left.val == max) || (cur.right != null && cur.right.val == max)) {
return cur;
}
cur.val = max;
}
// If p/q is left/right, return root
if (cur.left != null && cur.left.val == max && cur.right != null && cur.right.val == max) {
return cur;
}
// Pass MAX_VALUE upwards
if ((cur.left != null && cur.left.val == max) || (cur.right != null && cur.right.val == max)) {
cur.val = max;
}
pre = cur;
cur = null;
} else {
st.push(cur);
cur = cur.right;
}
}
return null;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Python
Recursive Version 1
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root == q or root == p or root is None:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left is not None and right is not None:
return root
if left is None and right is not None:
return right
elif left is not None and right is None:
return left
else:
return None
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Recursive Version 2 (Simplified)
class Solution:
def lowestCommonAncestor(self, root, p, q):
if root == q or root == p or root is None:
return root
left = self.lowestCommonAncestor(root.left, p, q)
right = self.lowestCommonAncestor(root.right, p, q)
if left is not None and right is not None:
return root
if left is None:
return right
return left
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Go
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
// check
if root == nil {
return root
}
// If equal, return the root node directly
if root == p || root == q {
return root
}
// Divide
left := lowestCommonAncestor(root.Left, p, q)
right := lowestCommonAncestor(root.Right, p, q)
// Conquer
// If both sides are non-null, the root is the ancestor
if left != nil && right != nil {
return root
}
if left != nil {
return left
}
if right != nil {
return right
}
return nil
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# JavaScript
var lowestCommonAncestor = function(root, p, q) {
// Using recursion
// Need to traverse from bottom to top, so we use postorder traversal
// 1. Define the recursive function
const travelTree = function(root,p,q) {
// 2. Define the recursion termination condition
if(root === null || root === p || root === q) {
return root;
}
// 3. Define the logic for single-layer recursion
let left = travelTree(root.left,p,q);
let right = travelTree(root.right,p,q);
if(left !== null && right !== null) {
return root;
}
if(left === null) {
return right;
}
return left;
}
return travelTree(root,p,q);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# TypeScript
function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
if (root === null || root === p || root === q) return root;
const left = lowestCommonAncestor(root.left, p, q);
const right = lowestCommonAncestor(root.right, p, q);
if (left !== null && right !== null) return root;
if (left !== null) return left;
if (right !== null) return right;
return null;
};
2
3
4
5
6
7
8
9
# Scala
object Solution {
def lowestCommonAncestor(root: TreeNode, p: TreeNode, q: TreeNode): TreeNode = {
// Recursive end condition
if (root == null || root == p || root == q) {
return root
}
var left = lowestCommonAncestor(root.left, p, q)
var right = lowestCommonAncestor(root.right, p, q)
if (left != null && right != null) return root
if (left == null) return right
left
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Rust
impl Solution {
pub fn lowest_common_ancestor(
root: Option<Rc<RefCell<TreeNode>>>,
p: Option<Rc<RefCell<TreeNode>>>,
q: Option<Rc<RefCell<TreeNode>>>,
) -> Option<Rc<RefCell<TreeNode>>> {
if root.is_none() {
return root;
}
if Rc::ptr_eq(root.as_ref().unwrap(), p.as_ref().unwrap())
|| Rc::ptr_eq(root.as_ref().unwrap(), q.as_ref().unwrap()) {
return root;
}
let left = Self::lowest_common_ancestor(
root.as_ref().unwrap().borrow().left.clone(),
p.clone(),
q.clone(),
);
let right =
Self::lowest_common_ancestor(root.as_ref().unwrap().borrow().right.clone(), p, q);
match (&left, &right) {
(None, Some(_)) => right,
(Some(_), Some(_)) => root,
_ => left,
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# C#
public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q)
{
if (root == null || root == p || root == q) return root;
TreeNode left = LowestCommonAncestor(root.left, p, q);
TreeNode right = LowestCommonAncestor(root.right, p, q);
if (left != null && right != null) return root;
if (left == null && right != null) return right;
if (left != null && right == null) return left;
return null;
}
2
3
4
5
6
7
8
9
10
