222. Count Complete Tree Nodes

LeetCode Problem Link (opens new window)

Given a complete binary tree, count the number of nodes.

Example 1:

• Input: root = [1,2,3,4,5,6]
• Output: 6

Example 2:

• Input: root = []
• Output: 0

Example 3:

• Input: root = [1]
• Output: 1

Constraints:

• The number of nodes in the tree is in the range [0, 5 * 10^4].
• 0 <= Node.val <= 5 * 10^4
• The input tree is guaranteed to be a complete binary tree.

Approach

This article provides both the approach for a regular binary tree as well as an approach that utilizes the properties of a complete binary tree.

Regular Binary Tree

First, we solve it using the logic of a regular binary tree.

The recursive method and iterative method for this problem are similar to those used in calculating the depth of a binary tree. For the iterative method, slightly modifying the template for 0102.Binary Tree Level Order Traversal (opens new window) will allow us to record the number of nodes.

The recursive order is still post-order (left-right-root).

Recursive

If you are not familiar with calculating the depth of a binary tree, you can refer to this article: 0104.Maximum Depth of Binary Tree (opens new window).

1. Determine the parameters and return value of the recursive function. The parameter is the root node of the tree to be passed in, and the return will be the number of nodes in the binary tree with that node as the root, so the return type will be int.

Here is the code:

int getNodesNum(TreeNode* cur) {

2. Determine the termination condition. If the node is NULL, it returns 0, indicating the number of nodes is 0.

Here is the code:

if (cur == NULL) return 0;

3. Determine the single level recursion logic. First, find the number of nodes in its left subtree, then in the right subtree. Finally, sum them up and add one (because the current middle node is also counted) to get the number of nodes in the binary tree with the current node as the root.

Here is the code:

int leftNum = getNodesNum(cur->left);      // left
int rightNum = getNodesNum(cur->right);    // right
int treeNum = leftNum + rightNum + 1;      // root
return treeNum;

Therefore, the entire C++ code is as follows:

// Version 1
class Solution {
private:
    int getNodesNum(TreeNode* cur) {
        if (cur == NULL) return 0;
        int leftNum = getNodesNum(cur->left);      // left
        int rightNum = getNodesNum(cur->right);    // right
        int treeNum = leftNum + rightNum + 1;      // root
        return treeNum;
    }
public:
    int countNodes(TreeNode* root) {
        return getNodesNum(root);
    }
};

Code after simplification:

// Version 2
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == NULL) return 0;
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};

• Time Complexity: O(n)
• Space Complexity: O(log n), considering the space occupied by the recursive system stack.

Most online resources use this simplified code version, but I do not recommend following this approach. The code is indeed concise, but it hides some details, making it difficult to understand the traversal order, so beginners are advised to learn from Version 1 to build a solid foundation.

Iterative

If you are not familiar with level-order traversal of binary trees, you can refer to this article: 0102.Binary Tree Level Order Traversal (opens new window).

In this case, modify only slightly, add a variable result to count the number of nodes.

class Solution {
public:
    int countNodes(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        int result = 0;
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                result++;   // record the number of nodes
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return result;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(n)

Complete Binary Tree

The above methods are based on regular binary trees. If you're not familiar with the properties of complete binary trees, you can refer to this article: Binary Tree Basics (opens new window). This article details the characteristics of various binary trees.

In a complete binary tree, except for the last level, all levels are fully filled with nodes, and all nodes in the last level are concentrated on the leftmost side. If the last level is h, then this level includes from 1 to 2^(h-1) nodes.

It's crucial to understand the definition of complete binary trees accurately.

I’ll give a typical example as stated in the problem:

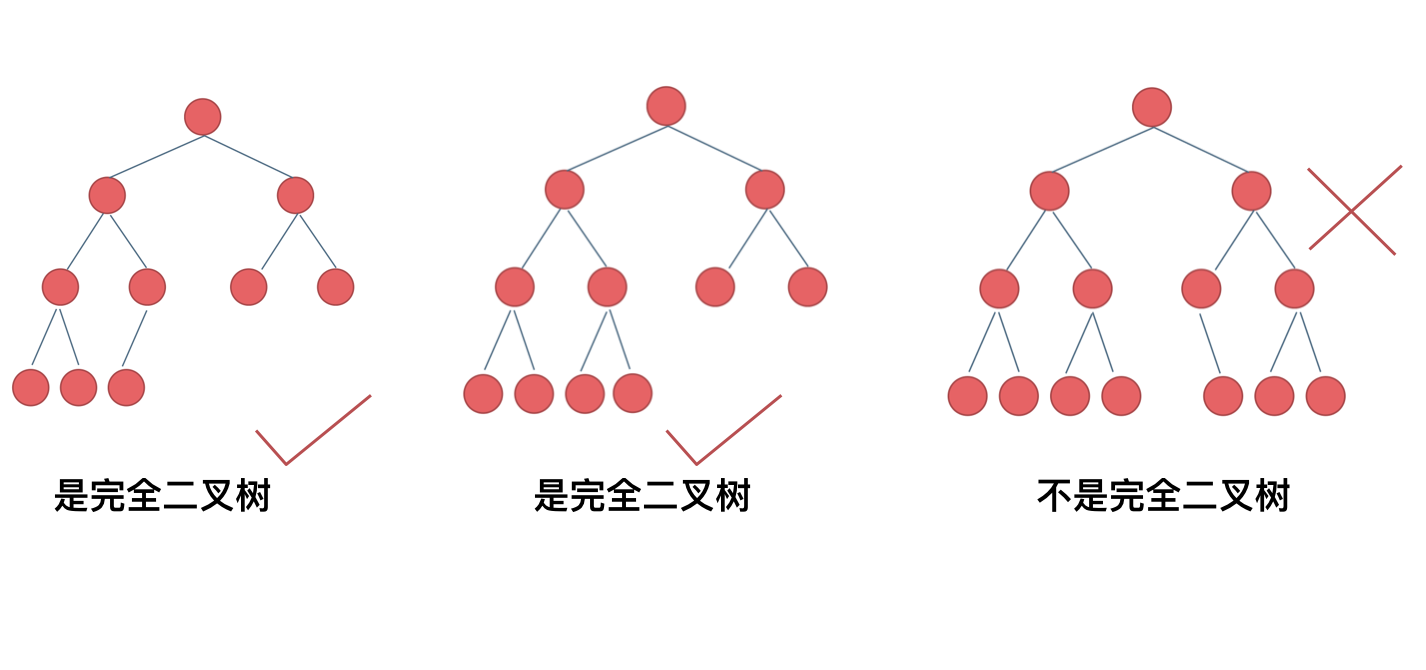
A complete binary tree has two situations, case one: a full binary tree, case two: the last level of leaf nodes is not full.

For case one, you can directly use the formula 2^(depth) - 1 to calculate, note here that the root node depth is 1.

For case two, recurse to left child and right child respectively, until some depth it will either have a left child or right child as a full binary tree, then you can calculate the number of nodes using case one.

Complete binary tree (one) as shown:

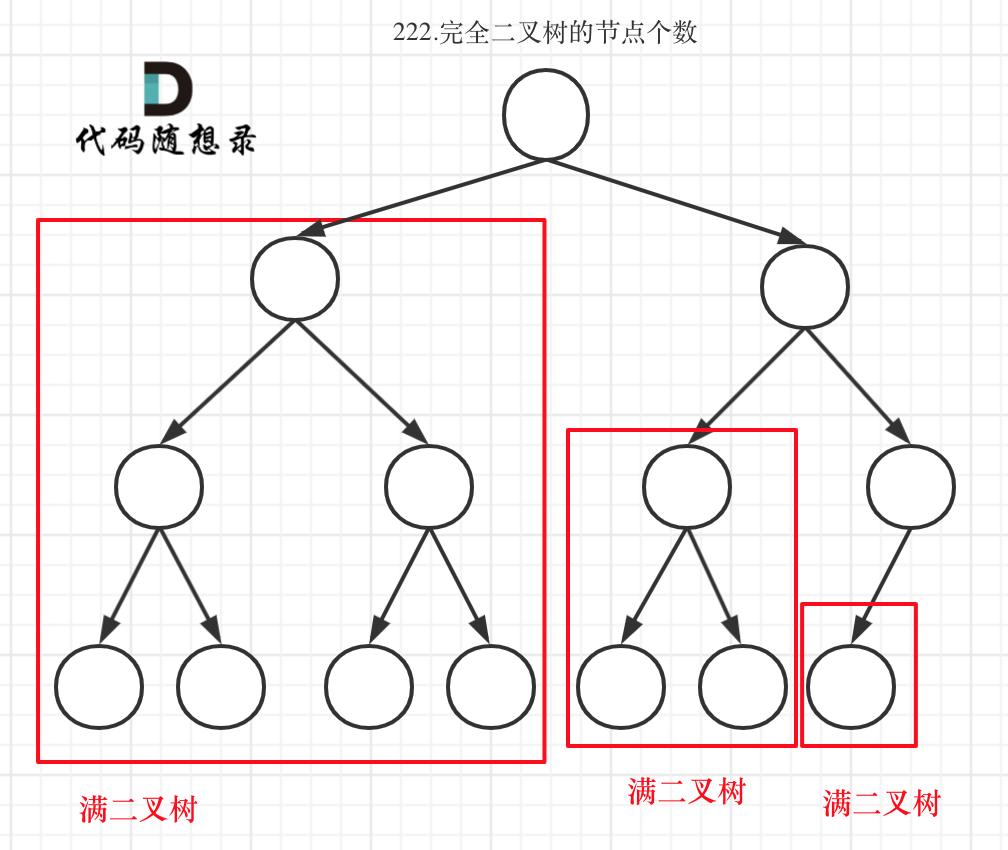
Complete binary tree (two) as shown:

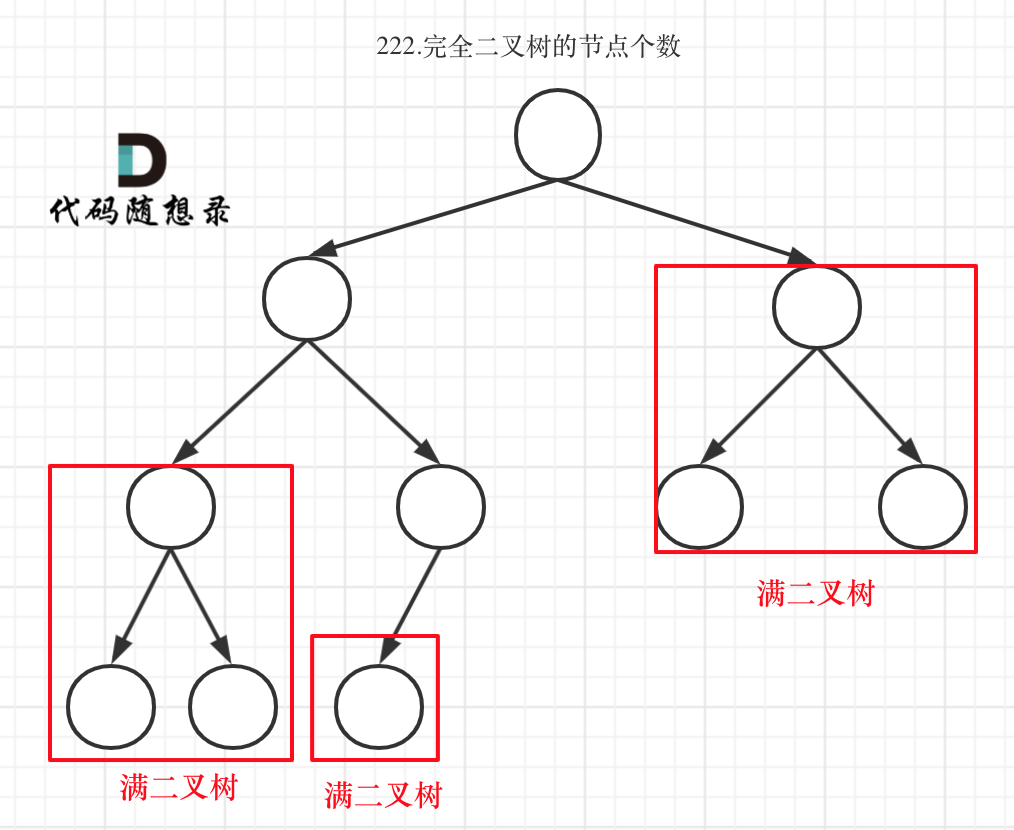
It can be seen that if the entire tree is not a full binary tree, simply recurse its left and right child until a full binary tree is encountered. Use the formula to calculate the number of nodes for this subtree (full binary tree).

How to determine whether a left subtree or right subtree is a full binary tree?

In a complete binary tree, if the depth of the left recursion is equal to the depth of the right recursion, then it is a full binary tree. As shown:

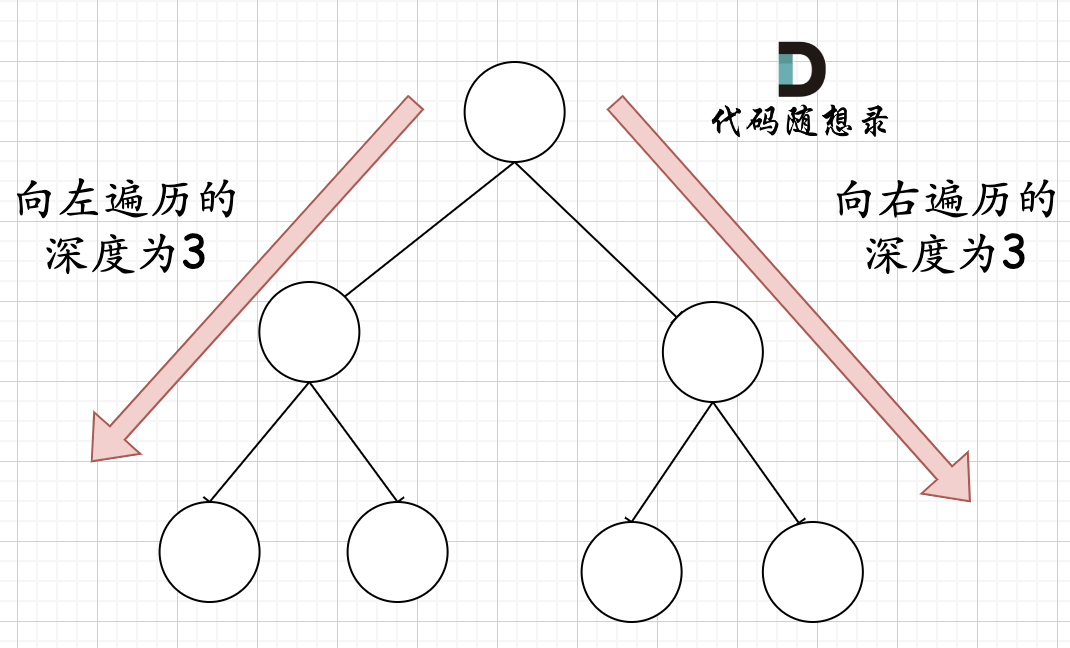
In a complete binary tree, if the depth of left recursion is not equal to the depth of right recursion, it's not a full binary tree, as shown:

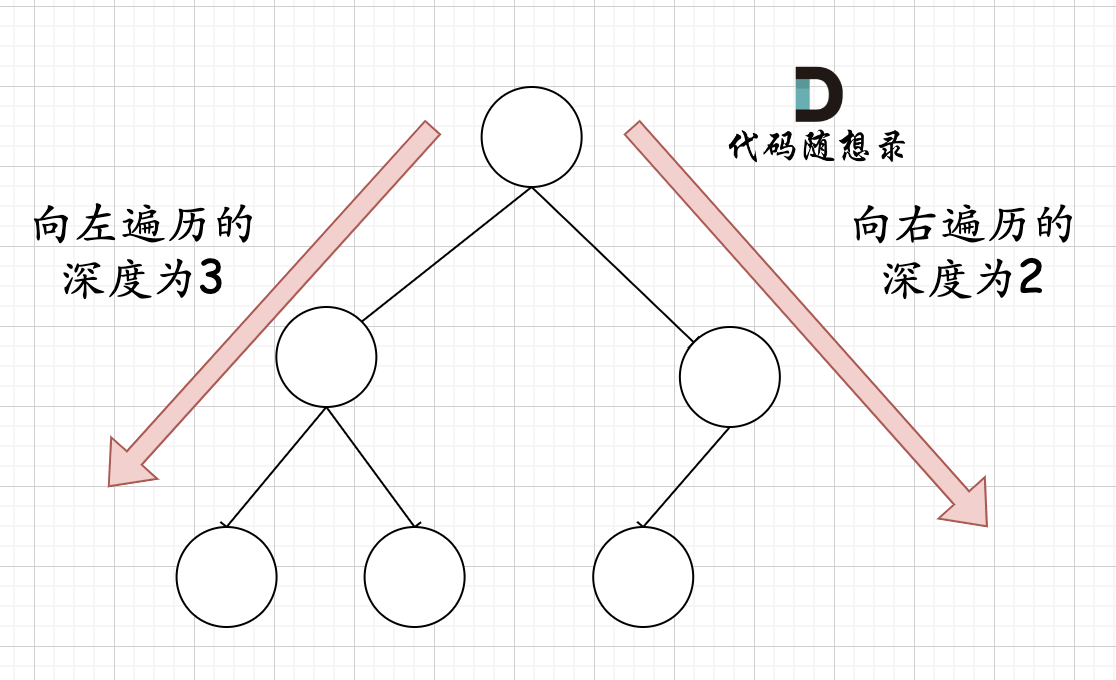
And if you think such cases can occur, you might misunderstand complete binary tree! The above binary tree is not a complete binary tree at all!

Determine whether the subtree is a full binary tree. If so, use the formula to calculate the number of nodes for this subtree (full binary tree). If not, continue recursion. The base case for recursion should be:

if (root == nullptr) return 0; 
// Begin determining if a subtree is a full binary tree based on left depth equals right depth
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // Initializing to 0 purposefully for the calculation of exponentiation
while (left) {  // Find left subtree depth
    left = left->left;
    leftDepth++;
}
while (right) { // Find right subtree depth
    right = right->right;
    rightDepth++;
}
if (leftDepth == rightDepth) {
    return (2 << leftDepth) - 1; // Note (2<<1) is equivalent to 2^2, return the number of nodes in a full binary subtree
}

For the third part of recursion in single-level logic use (can be seen as post-order traversal):

int leftTreeNum = countNodes(root->left);       // left
int rightTreeNum = countNodes(root->right);     // right
int result = leftTreeNum + rightTreeNum + 1;    // root
return result;

Simplified code:

return countNodes(root->left) + countNodes(root->right) + 1; 

Finally, the complete C++ code is as follows:

class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr) return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftDepth = 0, rightDepth = 0; // Initializing to 0 purposefully for calculation of exponentiation
        while (left) {  // Find left subtree depth
            left = left->left;
            leftDepth++;
        }
        while (right) { // Find right subtree depth
            right = right->right;
            rightDepth++;
        }
        if (leftDepth == rightDepth) {
            return (2 << leftDepth) - 1; // Note (2<<1) is equivalent to 2^2, hence leftDepth is initialized to 0
        }
        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

• Time Complexity: O(log n × log n)
• Space Complexity: O(log n)

Other Language Versions

Java:

class Solution {
    // General recursive method
    public int countNodes(TreeNode root) {
        if(root == null) {
            return 0;
        }
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

class Solution {
    // Iterative method
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int result = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size-- > 0) {
                TreeNode cur = queue.poll();
                result++;
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return result;
    }
}

class Solution {
    /**
     * Specific solution for complete binary tree
     *
     * Number of nodes in a full binary tree: 2^depth - 1
     */
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        TreeNode left = root.left;
        TreeNode right = root.right;
        int leftDepth = 0, rightDepth = 0; // Initializing to 0 purposefully for calculation of exponentiation
        while (left != null) {  // Find left subtree depth
            left = left.left;
            leftDepth++;
        }
        while (right != null) { // Find right subtree depth
            right = right.right;
            rightDepth++;
        }
        if (leftDepth == rightDepth) {
            return (2 << leftDepth) - 1; // Note (2<<1) is 2^2, hence leftDepth is initialized to 0
        }
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

Python:

Recursive method:

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        return self.getNodesNum(root)
        
    def getNodesNum(self, cur):
        if not cur:
            return 0
        leftNum = self.getNodesNum(cur.left) # left
        rightNum = self.getNodesNum(cur.right) # right
        treeNum = leftNum + rightNum + 1 # root
        return treeNum

Simplified recursive method:

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if not root:
            return 0
        return 1 + self.countNodes(root.left) + self.countNodes(root.right)

Iterative method:

import collections
class Solution:
    def countNodes(self, root: TreeNode) -> int:
        queue = collections.deque()
        if root:
            queue.append(root)
        result = 0
        while queue:
            size = len(queue)
            for i in range(size):
                node = queue.popleft()
                result += 1 # count the nodes
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        return result

Complete binary tree:

class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if not root:
            return 0
        left = root.left
        right = root.right
        leftDepth = 0 # Initializing to 0 purposefully for calculation of exponentiation
        rightDepth = 0
        while left: # find left subtree depth
            left = left.left
            leftDepth += 1
        while right: # find right subtree depth
            right = right.right
            rightDepth += 1
        if leftDepth == rightDepth:
            return (2 << leftDepth) - 1 # Note (2<<1) is 2^2, hence leftDepth is initialized to 0
        return self.countNodes(root.left) + self.countNodes(root.right) + 1

Complete binary tree method 2:

class Solution: # Utilize complete binary tree characteristics
    def countNodes(self, root: TreeNode) -> int:
        if not root: return 0
        count = 1
        left = root.left; right = root.right
        while left and right:
            count+=1
            left = left.left; right = right.right
        if not left and not right: # If both reach the end, it is a full binary tree, otherwise it's not
            return 2**count-1
        return 1+self.countNodes(root.left)+self.countNodes(root.right)  

Complete binary tree method 3:

class Solution: # Utilize complete binary tree characteristics
    def countNodes(self, root: TreeNode) -> int:
        if not root: return 0
        count = 0
        left = root.left; right = root.right
        while left and right:
            count+=1
            left = left.left; right = right.right
        if not left and not right: # If both reach the end, it is a full binary tree, otherwise it's not
            return (2<<count)-1
        return 1+self.countNodes(root.left)+self.countNodes(root.right)  

Go:

Recursive version:

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
// This problem directly asks for the number of nodes, so simply store the result.
func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    res := 1
    if root.Right != nil {
        res += countNodes(root.Right)
    }
    if root.Left != nil {
        res += countNodes(root.Left)
    }
    return res
}

Recursive solution using complete binary tree properties:

func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    leftH, rightH := 0, 0
    leftNode := root.Left
    rightNode := root.Right
    while leftNode != nil {
        leftNode = leftNode.Left
        leftH++
    }
    while rightNode != nil {
        rightNode = rightNode.Right
        rightH++
    }
    if leftH == rightH {
        return (2 << leftH) - 1
    }
    return countNodes(root.Left) + countNodes(root.Right) + 1
}

Iterative method:

func countNodes(root *TreeNode) int {
    if root == nil {
        return 0
    }
    q := list.New()
    q.PushBack(root)
    res := 0
    while q.Len() > 0 {
        n := q.Len()
        for i := 0; i < n; i++ {
            node := q.Remove(q.Front()).(*TreeNode)
            if node.Left != nil {
                q.PushBack(node.Left)
            }
            if node.Right != nil {
                q.PushBack(node.Right)
            }
            res++
        }
    }
    return res 
}

JavaScript:

Recursive version:

var countNodes = function(root) {
    // Recursive function to calculate the number of binary tree nodes
    // 1. Determine the recursive function parameters
    const getNodeSum = function(node) {
    // 2. Determine the termination condition
        if(node === null) {
            return 0;
        }
    // 3. Determine the logic for single-layer recursion
        let leftNum = getNodeSum(node.left);
        let rightNum = getNodeSum(node.right);
        return leftNum + rightNum + 1;
    }
    return getNodeSum(root);
};

Iterative (level-order traversal) version:

var countNodes = function(root) {
    // Level-order traversal
    let queue = [];
    if(root === null) {
        return 0;
    }
    queue.push(root);
    let nodeNums = 0;
    while(queue.length) {
        let length = queue.length;
        while(length--) {
            let node = queue.shift();
            nodeNums++;
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return nodeNums;
};

Utilizing complete binary tree properties:

var countNodes = function(root) {
    // Utilize the properties of a complete binary tree
    if(root === null) {
        return 0;
    }
    let left = root.left;
    let right = root.right;
    let leftDepth = 0, rightDepth = 0;
    while(left) {
        left = left.left;
        leftDepth++;
    }
    while(right) {
        right = right.right;
        rightDepth++;
    }
    if(leftDepth == rightDepth) {
        return Math.pow(2, leftDepth+1) - 1;
    }
    return countNodes(root.left) + countNodes(root.right) + 1;
};

TypeScript:

Recursive method

function countNodes(root: TreeNode | null): number {
    if (root === null) return 0;
    return 1 + countNodes(root.left) + countNodes(root.right);
};

Iterative method

function countNodes(root: TreeNode | null): number {
    let helperQueue: TreeNode[] = [];
    let resCount: number = 0;
    let tempNode: TreeNode;
    if (root !== null) helperQueue.push(root);
    while (helperQueue.length > 0) {
        for (let i = 0, length = helperQueue.length; i < length; i++) {
            tempNode = helperQueue.shift()!;
            resCount++;
            if (tempNode.left) helperQueue.push(tempNode.left);
            if (tempNode.right) helperQueue.push(tempNode.right);
        }
    }
    return resCount;
};

Utilizing complete binary tree properties

function countNodes(root: TreeNode | null): number {
    if (root === null) return 0;
    let left: number = 0,
        right: number = 0;
    let curNode: TreeNode | null= root;
    while (curNode !== null) {
        left++;
        curNode = curNode.left;
    }
    curNode = root;
    while (curNode !== null) {
        right++;
        curNode = curNode.right;
    }
    if (left === right) {
        return 2 ** left - 1;
    }
    return 1 + countNodes(root.left) + countNodes(root.right);
};

C:

Recursive method:

int countNodes(struct TreeNode* root) {
    // if the input node doesn't exist, return 0
    if(!root)
        return 0;
    // calculate the total nodes of left and right subtrees
    int leftCount = countNodes(root->left);
    int rightCount = countNodes(root->right);
    // return the total node count of the left and right subtrees + 1
    return leftCount + rightCount + 1;
}

int countNodes(struct TreeNode* root){
    return getNodes(root);
}

Iterative method:

int countNodes(struct TreeNode* root){
    // record the total number of nodes
    int totalNum = 0;
    // allocate memory for the stack
    struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 100);
    int stackTop = 0;
    // if the root node is not NULL, push it onto the stack. If it's NULL, no traversal occurs, return 0
    if(root)
        stack[stackTop++] = root;
    // if there are nodes in the stack, perform traversal
    while(stackTop) {
        // take the top element from the stack
        struct TreeNode* tempNode = stack[--stackTop];
        // increment the node total
        totalNum++;
        // if the top node has left or right children, push them onto the stack
        if(tempNode->left)
            stack[stackTop++] = tempNode->left;
        if(tempNode->right)
            stack[stackTop++] = tempNode->right;
    }
    return totalNum;
}

Full binary tree:

int countNodes(struct TreeNode* root){
    if(!root)
        return 0;
    int leftDepth = 0;
    int rightDepth = 0;
    struct TreeNode* rightNode = root->right;
    struct TreeNode* leftNode = root->left;
    // find left subtree depth
    while(leftNode) {
        leftNode = leftNode->left;
        leftDepth++;
    }

    // find right subtree depth
    while(rightNode) {
        rightNode = rightNode->right;
        rightDepth++;
    }
    // if left and right subtree depths are the same, it's a full binary tree. Node count is 2^height-1
    if(rightDepth == leftDepth) {
        return (2 << leftDepth) - 1;
    }
    // otherwise, return the node count of left and right subtrees + 1
    return countNodes(root->right) + countNodes(root->left) + 1;
}

Swift:

Recursive

func countNodes(_ root: TreeNode?) -> Int {
    return _countNodes(root)
}
func _countNodes(_ root: TreeNode?) -> Int {
    guard let root = root else {
        return 0
    }
    let leftCount = _countNodes(root.left)
    let rightCount = _countNodes(root.right)
    return 1 + leftCount + rightCount
}

Level-order traversal

func countNodes(_ root: TreeNode?) -> Int {
    guard let root = root else {
        return 0
    }
    var res = 0
    var queue = [TreeNode]()
    queue.append(root)
    while !queue.isEmpty {
        let size = queue.count
        for _ in 0 ..< size {
            let node = queue.removeFirst()
            res += 1
            if let left = node.left {
                queue.append(left)
            }
            if let right = node.right {
                queue.append(right)
            }
        }
    }
    return res
}

Utilizing the properties of a complete binary tree

func countNodes(_ root: TreeNode?) -> Int {
    guard let root = root else {
        return 0
    }
    var leftNode = root.left
    var rightNode = root.right
    var leftDepth = 0
    var rightDepth = 0
    while leftNode != nil {
        leftNode = leftNode!.left
        leftDepth += 1
    }
    while rightNode != nil {
        rightNode = rightNode!.right
        rightDepth += 1
    }
    if leftDepth == rightDepth {
        return (2 << leftDepth) - 1
    }
    return countNodes(root.left) + countNodes(root.right) + 1
}

Scala:

Recursive:

object Solution {
  def countNodes(root: TreeNode): Int = {
    if(root == null) return 0
    1 + countNodes(root.left) + countNodes(root.right)
  }
}

Level-order traversal:

object Solution {
  import scala.collection.mutable
  def countNodes(root: TreeNode): Int = {
    if (root == null) return 0
    val queue = mutable.Queue[TreeNode]()
    var node = 0
    queue.enqueue(root)
    while (!queue.isEmpty) {
      val len = queue.size
      for (i <- 0 until len) {
        node += 1
        val curNode = queue.dequeue()
        if (curNode.left != null) queue.enqueue(curNode.left)
        if (curNode.right != null) queue.enqueue(curNode.right)
      }
    }
    node
  }
}

Utilizing complete binary tree properties:

object Solution {
  def countNodes(root: TreeNode): Int = {
    if (root == null) return 0
    var leftNode = root.left
    var rightNode = root.right
    // depth traversal
    var leftDepth = 0
    while (leftNode != null) {
      leftDepth += 1
      leftNode = leftNode.left
    }
    var rightDepth = 0
    while (rightNode != null) {
      rightDepth += 1
      rightNode = rightNode.right
    }
    // if depths are the same, it's a full binary tree
    if (leftDepth == rightDepth) {
      return (2 << leftDepth) - 1
    }
    // if not, continue recursion
    countNodes(root.left) + countNodes(root.right) + 1
  }
}

Rust:

Recursive:

use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    pub fn count_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        if root.is_none() {
            return 0;
        }
        1 + Self::count_nodes(Rc::clone(root.as_ref().unwrap()).borrow().left.clone())
            + Self::count_nodes(root.unwrap().borrow().right.clone())
    }
}

Iterative:

use std::rc::Rc;
use std::cell::RefCell;
use std::collections::VecDeque;
impl Solution {
    pub fn count_nodes(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut res = 0;
        let mut queue = VecDeque::new();
        if root.is_some() {
            queue.push_back(root);
        }
        while !queue.is_empty() {
            for _ in 0..queue.len() {
                let node = queue.pop_front().unwrap().unwrap();
                if node.borrow().left.is_some() {
                    queue.push_back(node.borrow().left.clone());
                }
                if node.borrow().right.is_some() {
                    queue.push_back(node.borrow().right.clone());
                }
                res += 1;
            }
        }
        res
    }
}

C#

// Recursive
public int CountNodes(TreeNode root)
{
    if (root == null) return 0;
    var left = root.left;
    var right = root.right;
    int leftDepth = 0, rightDepth = 0;
    while (left != null)
    {
        left = left.left;
        leftDepth++;
    }
    while (right != null)
    {
        right = right.right;
        rightDepth++;
    }
    if (leftDepth == rightDepth)
        return (int)Math.Pow(2, leftDepth+1) - 1;
    return CountNodes(root.left) + CountNodes(root.right) + 1;

}