Same approach as finding the maximum depth?
# 111. Minimum Depth of Binary Tree
LeetCode Problem Link (opens new window)
Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree [3,9,20,null,null,15,7],
Return its minimum depth as 2.
# Approach
Having read the solution for 0104.Maximum Depth of Binary Tree (opens new window), let's now look at how to compute the minimum depth.
Initially, it might seem that finding the maximum depth and the minimum depth in a binary tree is quite similar, but there are noticeable differences.
In this problem, either pre-order traversal or post-order traversal can be used. In pre-order traversal, the depth is calculated, while in post-order traversal, the height is computed.
- Depth of a binary tree node: The length of the longest simple path (or the number of nodes, depending on whether depth starts from 0 or 1) from the root node to that node.
- Height of a binary tree node: The length of the longest simple path (or the number of nodes, depending on whether height starts from 0 or 1) from that node to a leaf node.
Using post-order traversal essentially calculates the minimum distance from the root to a leaf node, which is indeed the minimum depth.
Because of the logic for handling child nodes, maximum and minimum depth calculations differ. Consider this diagram:
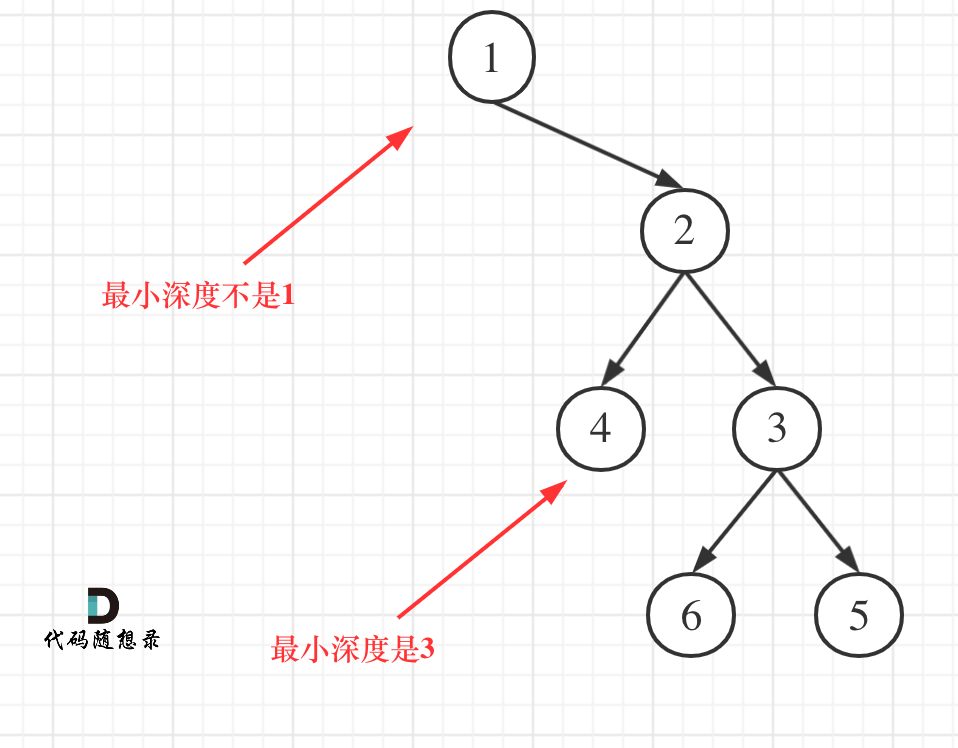
The key point is, the task is asking for the shortest path to a leaf node, not a node with potentially one child.
# Recursive Method
Let's go through the recursive solution in three steps:
- Determine the parameters and return type of the recursive function.
The parameters should include the root node of the tree, and the return type should be an integer representing the depth.
int getDepth(TreeNode* node)
1
- Define the termination condition.
The termination condition should return 0 when encountering a null node, indicating the height is 0 for this node.
if (node == NULL) return 0;
1
- Define the logic of a single recursion layer.
Unlike calculating the maximum depth, finding the minimum depth requires additional logic to handle cases where one subtree may be absent, as shown in the previous image.
If the left subtree is absent but the right subtree is present, the minimum depth becomes 1 + rightDepth. Similarly, if the right subtree is absent, the minimum depth is 1 + leftDepth. If both child nodes exist, return 1 + min(leftDepth, rightDepth).
int leftDepth = getDepth(node->left); // Left
int rightDepth = getDepth(node->right); // Right
// If left subtree is absent, right must contribute to the depth
if (node->left == NULL && node->right != NULL) {
return 1 + rightDepth;
}
// If right subtree is absent, left must contribute to the depth
if (node->left != NULL && node->right == NULL) {
return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
This approach, which uses post-order traversal (left-right-center), emphasizes how the difference between calculating maximum and minimum depth primarily lies in logic for handling null child nodes.
The complete recursive solution is as follows:
class Solution {
public:
int getDepth(TreeNode* node) {
if (node == NULL) return 0;
int leftDepth = getDepth(node->left); // Left
int rightDepth = getDepth(node->right); // Right
// Center
// When left subtree is absent, use right subtree
if (node->left == NULL && node->right != NULL) {
return 1 + rightDepth;
}
// When right subtree is absent, use left subtree
if (node->left != NULL && node->right == NULL) {
return 1 + leftDepth;
}
int result = 1 + min(leftDepth, rightDepth);
return result;
}
int minDepth(TreeNode* root) {
return getDepth(root);
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Here's a more concise version of the recursive code:
class Solution {
public:
int minDepth(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right != NULL) {
return 1 + minDepth(root->right);
}
if (root->left != NULL && root->right == NULL) {
return 1 + minDepth(root->left);
}
return 1 + min(minDepth(root->left), minDepth(root->right));
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
This concise version hides some of the traversal type, so if you are not yet familiar with binary tree operations, it's better to stick to the detailed version.
Pre-order traversal method:
class Solution {
private:
int result;
void getdepth(TreeNode* node, int depth) {
if (node == nullptr) { // Function termination condition
return;
}
if (node -> left == nullptr && node->right == nullptr) {
result = min(result, depth); // Center: check if it's a leaf node
}
if (node->left) { // Left
getdepth(node->left, depth + 1);
}
if (node->right) { // Right
getdepth(node->right, depth + 1);
}
return ;
}
public:
int minDepth(TreeNode* root) {
if (root == nullptr) {
return 0;
}
result = INT_MAX;
getdepth(root, 1);
return result;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Iterative Method
Unlike 0104.Maximum Depth of Binary Tree (opens new window), this problem can also be solved using level-order traversal. The approach remains similar.
If you're unfamiliar with level-order traversal, refer to this: 0102.Binary Tree Level Order Traversal (opens new window).
Take note: Only when both left and right children are absent are you at the actual lowest point.
Here's the iterative implementation with detailed comments:
class Solution {
public:
int minDepth(TreeNode* root) {
if (root == NULL) return 0;
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()) {
int size = que.size();
depth++; // Record the minimum depth
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
if (!node->left && !node->right) { // If both children are null, you're at the lowest level, exit
return depth;
}
}
}
return depth;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Other Language Versions
# Java:
class Solution {
/**
* Recursive method, more complex than MaxDepth
* Because the minimum depth is from the root node to the nearest **leaf node**
*/
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftDepth = minDepth(root.left);
int rightDepth = minDepth(root.right);
if (root.left == null) {
return rightDepth + 1;
}
if (root.right == null) {
return leftDepth + 1;
}
// Both child nodes are not null
return Math.min(leftDepth, rightDepth) + 1;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
/**
* Recursive, inspired by the recursive method of the maximum depth of a binary tree
* This question asks for the minimum depth, the minimum depth being the depth from the root node to the leaf node.
*/
int depth = 0;
int minDepth = Integer.MAX_VALUE;
public int minDepth(TreeNode root) {
dep(root);
return minDepth == Integer.MAX_VALUE ? 0 : minDepth;
}
void dep(TreeNode root){
if(root == null) return ;
// Start recursion, increase depth
depth++;
dep(root.left);
dep(root.right);
// This position means recursion has reached the leaf node, need to update the minimum depth minDepth
if(root.left == null && root.right == null)
minDepth = Math.min(minDepth , depth);
// End recursion, decrease depth
depth--;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
/**
* Iterative, level-order traversal
*/
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root);
int depth = 0;
while (!deque.isEmpty()) {
int size = deque.size();
depth++;
for (int i = 0; i < size; i++) {
TreeNode poll = deque.poll();
if (poll.left == null && poll.right == null) {
// It's a leaf node, return depth immediately because this value is the minimum
return depth;
}
if (poll.left != null) {
deque.offer(poll.left);
}
if (poll.right != null) {
deque.offer(poll.right);
}
}
}
return depth;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Python:
Recursive method (Version 1)
class Solution:
def getDepth(self, node):
if node is None:
return 0
leftDepth = self.getDepth(node.left) # Left
rightDepth = self.getDepth(node.right) # Right
# When the left subtree is empty and the right is not, it is not the lowest point
if node.left is None and node.right is not None:
return 1 + rightDepth
# When the right subtree is empty and the left is not, it is not the lowest point
if node.left is not None and node.right is None:
return 1 + leftDepth
result = 1 + min(leftDepth, rightDepth)
return result
def minDepth(self, root):
return self.getDepth(root)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Recursive method (Version 2)
class Solution:
def minDepth(self, root):
if root is None:
return 0
if root.left is None and root.right is not None:
return 1 + self.minDepth(root.right)
if root.left is not None and root.right is None:
return 1 + self.minDepth(root.left)
return 1 + min(self.minDepth(root.left), self.minDepth(root.right))
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
Recursive method (Version 3) pre-order
class Solution:
def __init__(self):
self.result = float('inf')
def getDepth(self, node, depth):
if node is None:
return
if node.left is None and node.right is None:
self.result = min(self.result, depth)
if node.left:
self.getDepth(node.left, depth + 1)
if node.right:
self.getDepth(node.right, depth + 1)
def minDepth(self, root):
if root is None:
return 0
self.getDepth(root, 1)
return self.result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Iterative method
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
depth = 0
queue = collections.deque([root])
while queue:
depth += 1
for _ in range(len(queue)):
node = queue.popleft()
if not node.left and not node.right:
return depth
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return depth
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Go:
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func min(a, b int) int {
if a < b {
return a;
}
return b;
}
// Recursive
func minDepth(root *TreeNode) int {
if root == nil {
return 0;
}
if root.Left == nil && root.Right != nil {
return 1 + minDepth(root.Right);
}
if root.Right == nil && root.Left != nil {
return 1 + minDepth(root.Left);
}
return min(minDepth(root.Left), minDepth(root.Right)) + 1;
}
// Iterative
func minDepth(root *TreeNode) int {
dep := 0;
queue := make([]*TreeNode, 0);
if root != nil {
queue = append(queue, root);
}
for l := len(queue); l > 0; {
dep++;
for ; l > 0; l-- {
node := queue[0];
if node.Left == nil && node.Right == nil {
return dep;
}
if node.Left != nil {
queue = append(queue, node.Left);
}
if node.Right != nil {
queue = append(queue, node.Right);
}
queue = queue[1:];
}
l = len(queue);
}
return dep;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# JavaScript:
Recursive method:
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth1 = function(root) {
if(!root) return 0;
// Return 1 if it's a leaf node
if(!root.left && !root.right) return 1;
// Only exists right child, recurse right child
if(!root.left) return 1 + minDepth(root.right);
// Only exists left child, recurse left child
if(!root.right) return 1 + minDepth(root.left);
return Math.min(minDepth(root.left), minDepth(root.right)) + 1;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative method:
/**
* @param {TreeNode} root
* @return {number}
*/
var minDepth = function(root) {
if(!root) return 0;
const queue = [root];
let dep = 0;
while(true) {
let size = queue.length;
dep++;
while(size--){
const node = queue.shift();
// Reached the first leaf node, return the current depth
if(!node.left && !node.right) return dep;
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# TypeScript:
Recursive method
function minDepth(root: TreeNode | null): number {
if (root === null) return 0;
if (root.left !== null && root.right === null) {
return 1 + minDepth(root.left);
}
if (root.left === null && root.right !== null) {
return 1 + minDepth(root.right);
}
return 1 + Math.min(minDepth(root.left), minDepth(root.right));
}
1
2
3
4
5
6
7
8
9
10
2
3
4
5
6
7
8
9
10
Iterative method
function minDepth(root: TreeNode | null): number {
let helperQueue: TreeNode[] = [];
let resMin: number = 0;
let tempNode: TreeNode;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
resMin++;
for (let i = 0, length = helperQueue.length; i < length; i++) {
tempNode = helperQueue.shift()!;
if (tempNode.left === null && tempNode.right === null) return resMin;
if (tempNode.left !== null) helperQueue.push(tempNode.left);
if (tempNode.right !== null) helperQueue.push(tempNode.right);
}
}
return resMin;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Swift:
Recursive
func minDepth(_ root: TreeNode?) -> Int {
guard let root = root else {
return 0
}
if root.left == nil && root.right != nil {
return 1 + minDepth(root.right)
}
if root.left != nil && root.right == nil {
return 1 + minDepth(root.left)
}
return 1 + min(minDepth(root.left), minDepth(root.right))
}
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
Iterative
func minDepth(_ root: TreeNode?) -> Int {
guard let root = root else {
return 0
}
var res = 0
var queue = [TreeNode]()
queue.append(root)
while !queue.isEmpty {
res += 1
for _ in 0 ..< queue.count {
let node = queue.removeFirst()
if node.left == nil && node.right == nil {
return res
}
if let left = node.left {
queue.append(left)
}
if let right = node.right {
queue.append(right)
}
}
}
return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Scala:
Recursive method:
object Solution {
def minDepth(root: TreeNode): Int = {
if (root == null) return 0
if (root.left == null && root.right != null) return 1 + minDepth(root.right)
if (root.left != null && root.right == null) return 1 + minDepth(root.left)
// If both sides are not null, take the minimum value
1 + math.min(minDepth(root.left), minDepth(root.right))
}
}
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
Iterative method:
object Solution {
import scala.collection.mutable
def minDepth(root: TreeNode): Int = {
if (root == null) return 0
var depth = 0
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
while (!queue.isEmpty) {
depth += 1
val len = queue.size
for (i <- 0 until len) {
val curNode = queue.dequeue()
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
if (curNode.left == null && curNode.right == null) return depth
}
}
depth
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Rust:
impl Solution {
// Recursive
pub fn min_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
if let Some(node) = root {
match (node.borrow().left.clone(), node.borrow().right.clone()) {
(Some(n1), None) => 1 + Self::min_depth(Some(n1)),
(None, Some(n2)) => 1 + Self::min_depth(Some(n2)),
(Some(n1), Some(n2)) => {
1 + std::cmp::min(Self::min_depth(Some(n1)), Self::min_depth(Some(n2)))
}
_ => 1,
}
} else {
0
}
}
// Iterative
// Requires use std::collections::VecDeque;
pub fn min_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
let mut queue = VecDeque::new();
if root.is_some() {
queue.push_back(root);
}
while !queue.is_empty() {
res += 1;
for _ in 0..queue.len() {
let node = queue.pop_front().unwrap().unwrap();
if node.borrow().left.is_none() && node.borrow().right.is_none() {
return res;
}
if node.borrow().left.is_some() {
queue.push_back(node.borrow().left.clone());
}
if node.borrow().right.is_some() {
queue.push_back(node.borrow().right.clone());
}
}
}
res
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# C#
// Recursive
public int MinDepth(TreeNode root)
{
if (root == null) return 0;
int left = MinDepth(root.left);
int right = MinDepth(root.right);
if (root.left == null && root.right != null)
return 1+right;
else if(root.left!=null && root.right == null)
return 1+left;
int res = 1 + Math.Min(left, right);
return res;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2
3
4
5
6
7
8
9
10
11
12
13
14
// Iterative
public int MinDepth(TreeNode root)
{
if (root == null) return 0;
int depth = 0;
var que = new Queue<TreeNode>();
que.Enqueue(root);
while (que.Count > 0)
{
int size = que.Count;
depth++;
for (int i = 0; i < size; i++)
{
var node = que.Dequeue();
if (node.left != null)
que.Enqueue(node.left);
if (node.right != null)
que.Enqueue(node.right);
if (node.left == null && node.right == null)
return depth;
}
}
return depth;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Copyright © 2025 keetcoder