# 98. Validate Binary Search Tree
LeetCode Problem Link (opens new window)
Given a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.

# Thought Process
It’s essential to know that, in an inorder traversal, the values of nodes in a binary search tree (BST) are sequential.
With this characteristic in mind, validating a binary search tree is the same as checking if a sequence is in ascending order.
# Recursive Method
You can recursively perform an inorder traversal to convert a binary search tree into an array, as shown in the code below:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // Convert the BST into a sorted array
traversal(root->right);
}
2
3
4
5
6
7
Then, simply check if the array is in order. Note that a binary search tree cannot have duplicate elements.
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// Note that it should be less than or equal to, as the BST cannot have duplicate elements.
if (vec[i] <= vec[i - 1]) return false;
}
return true;
2
3
4
5
6
Complete code is as follows:
class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // Convert the BST into a sorted array
traversal(root->right);
}
public:
bool isValidBST(TreeNode* root) {
vec.clear(); // Although not necessary on Leetcode, it's better to include this
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// Note that it should be less than or equal to, as the BST cannot have duplicate elements.
if (vec[i] <= vec[i - 1]) return false;
}
return true;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
In the code above, we convert the tree into an array to check it, which is the most straightforward method. However, you don’t need to convert it into an array; you can directly determine its order while recursively traversing.
This problem has two main traps:
- Trap 1
You cannot merely compare if the left node is less than the middle node and the right node is greater than the middle node.
A code like the following is incorrect:
if (root->val > root->left->val && root->val < root->right->val) {
return true;
} else {
return false;
}
2
3
4
5
We need to compare if all nodes in the left subtree are less than the middle node, and all nodes in the right subtree are greater than the middle node. Therefore, the above logic is wrong.
For example: the case [10,5,15,null,null,6,20]:
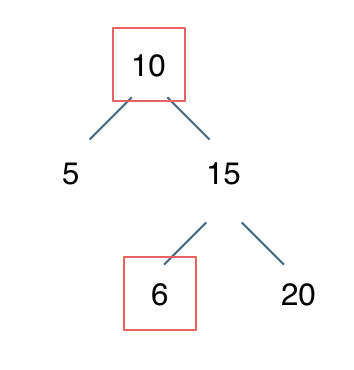
Node 10 is greater than left node 5 and less than right node 15, but there is a 6 in the right subtree, which is incorrect!
- Trap 2
The smallest node in the sample might be the minimum value of an integer. So using the smallest integer for comparison is also incorrect.
In this case, you can initialize the comparison element to the minimum value of long long.
If the root node’s val might be the smallest value of long long, what should you do? This will be answered in the article.
After understanding these traps, let's see how the code should be written:
Recursive Trilogy:
- Determine the recursive function, return value, and parameters
Define a global variable of type long long to compare traversed nodes’ order, because the backend test data has the minimum value of an integer, hence we define it as long long type and initialize it with the minimum value.
Note that the recursive function should have a bool return value, as we discussed in 0112. Path Sum (opens new window), when looking for a specific edge (or node), the recursive function has a bool return value.
This problem is similar: we are looking for a node that does not meet the criteria. If no such node is found, the whole tree is traversed. If such a node is found, return immediately.
Code snippet:
long long maxVal = LONG_MIN; // Because the backend test data had int’s minimum value
bool isValidBST(TreeNode* root)
2
- Determine the base cases
If the node is null, is it a valid BST?
Yes, it is!
Code snippet:
if (root == NULL) return true;
- Determine the single-layer recursion logic
Inorder traversal constantly updates maxVal. Once maxVal >= root->val is found, return false. Note that when elements are equal, it also returns false.
Code snippet:
bool left = isValidBST(root->left); // Left
// During inorder traversal, verify if the elements are in increasing order
if (maxVal < root->val) maxVal = root->val; // Middle
else return false;
bool right = isValidBST(root->right); // Right
return left && right;
2
3
4
5
6
7
8
The complete code:
class Solution {
public:
long long maxVal = LONG_MIN; // Because the backend test data had int’s minimum value
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
// During inorder traversal, verify if the elements are in increasing order
if (maxVal < root->val) maxVal = root->val;
else return false;
bool right = isValidBST(root->right);
return left && right;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Above, the code uses long long to ensure it handles backend test data that have the smallest integer values correctly.
If there’s test data featuring the smallest long long, what should be done?
You can’t initialize some smaller value, right? It’s advised to avoid initializing with the minimum value. Instead, find the value of the leftmost node for comparison.
Code snippet:
class Solution {
public:
TreeNode* pre = NULL; // To record the previous node
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
if (pre != NULL && pre->val >= root->val) return false;
pre = root; // Record the previous node
bool right = isValidBST(root->right);
return left && right;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Finally, this last code version seems a bit cleaner, and the thought process is clear.
# Iterative Method
You can use an iterative method to simulate inorder traversal of a binary tree. For those unfamiliar with pre-, in-, and post-order iterative methods, you may refer to Binary Tree Iterative Traversal (opens new window) and Unified Iterative Traversal of Binary Tree (opens new window).
Slight modifications to the iterative inorder traversal can accomplish this task. Here’s the code:
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL; // Record the previous node
while (cur != NULL || !st.empty()) {
if (cur != NULL) {
st.push(cur);
cur = cur->left; // Left
} else {
cur = st.top(); // Middle
st.pop();
if (pre != NULL && cur->val <= pre->val)
return false;
pre = cur; // Save the previous visited node
cur = cur->right; // Right
}
}
return true;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
In 0700. Search in a Binary Search Tree (opens new window), we wrote a wonderfully succinct iterative method. Why does that not work here? Because this problem is about validating a binary search tree.
# Summary
This problem is considered easy, but for those who are new to it, it can be challenging.
So beginners should not worry if they find simple problems baffling initially; it is a normal part of the learning curve. Everyone has a similar IQ.
Once you’ve done the basic types of problems and summarized them, ideas will naturally come to you. Keep pushing forward! 💪
# Other Language Versions
# Java
// Unified Iterative Implementation
class Solution {
public boolean isValidBST(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
if(root != null)
stack.add(root);
while(!stack.isEmpty()){
TreeNode curr = stack.peek();
if(curr != null){
stack.pop();
if(curr.right != null)
stack.add(curr.right);
stack.add(curr);
stack.add(null);
if(curr.left != null)
stack.add(curr.left);
}else{
stack.pop();
TreeNode temp = stack.pop();
if(pre != null && pre.val >= temp.val)
return false;
pre = temp;
}
}
return true;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
// Recursive
TreeNode max;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
// Left
boolean left = isValidBST(root.left);
if (!left) {
return false;
}
// Middle
if (max != null && root.val <= max.val) {
return false;
}
max = root;
// Right
boolean right = isValidBST(root.right);
return right;
}
}
class Solution {
// Iterative
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left; // Left
}
// Middle, process
TreeNode pop = stack.pop();
if (pre != null && pop.val <= pre.val) {
return false;
}
pre = pop;
root = pop.right; // Right
}
return true;
}
}
// Short Implementation: Recursive
class Solution {
public boolean isValidBST(TreeNode root) {
return validBST(Long.MIN_VALUE, Long.MAX_VALUE, root);
}
boolean validBST(long lower, long upper, TreeNode root) {
if (root == null) return true;
if (root.val <= lower || root.val >= upper) return false;
return validBST(lower, root.val, root.left) && validBST(root.val, upper, root.right);
}
}
// Short Implementation: Inorder Traversal
class Solution {
private long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if (root == null) {
return true;
}
if (!isValidBST(root.left)) {
return false;
}
if (root.val <= prev) { // Does not satisfy BST condition
return false;
}
prev = root.val;
return isValidBST(root.right);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
# Python
Recursive method (Version 1) utilizes the inorder sequential property, converting into an array
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.vec = []
def traversal(self, root):
if root is None:
return
self.traversal(root.left)
self.vec.append(root.val) # Convert the BST to a sorted array
self.traversal(root.right)
def isValidBST(self, root):
self.vec = [] # Clear the array
self.traversal(root)
for i in range(1, len(self.vec)):
# Note that it should be less than or equal to, as the BST cannot have duplicate elements.
if self.vec[i] <= self.vec[i - 1]:
return False
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Recursive method (Version 2) sets up a value of extreme small for comparison
class Solution:
def __init__(self):
self.maxVal = float('-inf') # Because the backend test data contain the minimum integer value
def isValidBST(self, root):
if root is None:
return True
left = self.isValidBST(root.left)
# During inorder traversal, verify if the elements are in increasing order
if self.maxVal < root.val:
self.maxVal = root.val
else:
return False
right = self.isValidBST(root.right)
return left and right
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Recursive method (Version 3) directly takes the smallest value in the tree
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.pre = None # To record the previous node
def isValidBST(self, root):
if root is None:
return True
left = self.isValidBST(root.left)
if self.pre is not None and self.pre.val >= root.val:
return False
self.pre = root # Record the previous node
right = self.isValidBST(root.right)
return left and right
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Iterative method
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root):
stack = []
cur = root
pre = None # To record the previous node
while cur is not None or len(stack) > 0:
if cur is not None:
stack.append(cur)
cur = cur.left # Left
else:
cur = stack.pop() # Middle
if pre is not None and cur.val <= pre.val:
return False
pre = cur # Save the previous visited node
cur = cur.right # Right
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Go
func isValidBST(root *TreeNode) bool {
// Even an empty tree is a valid search binary tree
if root == nil {
return true
}
// Given data limitations, we derive min and max
return check(root, math.MinInt64, math.MaxInt64)
}
func check(node *TreeNode, min, max int64) bool {
if node == nil {
return true
}
if min >= int64(node.Val) || max <= int64(node.Val) {
return false
}
// Recursively check both left and right subtrees, return true if both are valid
return check(node.Right, int64(node.Val), max) && check(node.Left, min, int64(node.Val))
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// Inorder Traversal Solution
func isValidBST(root *TreeNode) bool {
// Save the previous node
var prev *TreeNode
var travel func(node *TreeNode) bool
travel = func(node *TreeNode) bool {
if node == nil {
return true
}
leftRes := travel(node.Left)
// If the current value is less than or equal to the previous node's value, return false
if prev != nil && node.Val <= prev.Val {
return false
}
prev = node
rightRes := travel(node.Right)
return leftRes && rightRes
}
return travel(root)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# JavaScript
Auxiliary Array Solution
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isValidBST = function (root) {
let arr = [];
const buildArr = (root) => {
if (root) {
buildArr(root.left);
arr.push(root.val);
buildArr(root.right);
}
}
buildArr(root);
for (let i = 1; i < arr.length; ++i) {
if (arr[i] <= arr[i - 1])
return false;
}
return true;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Recursive Inorder Solution
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
let pre = null;
var isValidBST = function (root) {
let pre = null;
const inOrder = (root) => {
if (root === null)
return true;
let left = inOrder(root.left);
if (pre !== null && pre.val >= root.val)
return false;
pre = root;
let right = inOrder(root.right);
return left && right;
}
return inOrder(root);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Iterative Method:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
let pre = null;
var isValidBST = function (root) {
const queue = [];
let cur = root;
let pre = null;
while (cur !== null || queue.length !== 0) {
if (cur !== null) {
queue.push(cur);
cur = cur.left;
} else {
cur = queue.pop();
if (pre !== null && cur.val <= pre.val) {
return false;
}
pre = cur;
cur = cur.right;
}
}
return true;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# TypeScript
Auxiliary Array Solution:
function isValidBST(root: TreeNode | null): boolean {
const traversalArr: number[] = [];
function inorderTraverse(root: TreeNode | null): void {
if (root === null) return;
inorderTraverse(root.left);
traversalArr.push(root.val);
inorderTraverse(root.right);
}
inorderTraverse(root);
for (let i = 0, length = traversalArr.length; i < length - 1; i++) {
if (traversalArr[i] >= traversalArr[i + 1]) return false;
}
return true;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Recursive Inorder Solution:
function isValidBST(root: TreeNode | null): boolean {
let maxVal = -Infinity;
function inorderTraverse(root: TreeNode | null): boolean {
if (root === null) return true;
let leftValid: boolean = inorderTraverse(root.left);
if (!leftValid) return false;
if (maxVal < root.val) {
maxVal = root.val
} else {
return false;
}
let rightValid: boolean = inorderTraverse(root.right);
return leftValid && rightValid;
}
return inorderTraverse(root);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Iterative Method:
function isValidBST(root: TreeNode | null): boolean {
const queue: TreeNode[] = [];
let cur: TreeNode | null = root;
let pre: TreeNode | null = null;
while (cur !== null || queue.length !== 0) {
if (cur !== null) {
queue.push(cur);
cur = cur.left;
} else {
cur = queue.pop()!;
if (pre !== null && cur!.val <= pre.val) {
return false;
}
pre = cur;
cur = cur!.right;
}
}
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Scala
Auxiliary Array Solution:
object Solution {
import scala.collection.mutable
def isValidBST(root: TreeNode): Boolean = {
var arr = new mutable.ArrayBuffer[Int]()
// Recursive inorder traversal of binary tree, adding nodes to arr
def traversal(node: TreeNode): Unit = {
if (node == null) return
traversal(node.left)
arr.append(node.value)
traversal(node.right)
}
traversal(root)
// If the array is in ascending order, it indicates a BST
for (i <- 1 until arr.size) {
if (arr(i) <= arr(i - 1)) return false
}
true
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Recursive Inorder Solution:
object Solution {
def isValidBST(root: TreeNode): Boolean = {
var flag = true
var preValue:Long = Long.MinValue // Using Long type
def traversal(node: TreeNode): Unit = {
if (node == null || flag == false) return
traversal(node.left)
if (node.value > preValue) preValue = node.value
else flag = false
traversal(node.right)
}
traversal(root)
flag
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Rust
Recursive:
impl Solution {
pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
Self::valid_bst(i64::MIN, i64::MAX, root)
}
pub fn valid_bst(low: i64, upper: i64, root: Option<Rc<RefCell<TreeNode>>>) -> bool {
if root.is_none() {
return true;
}
let root = root.as_ref().unwrap().borrow();
if root.val as i64 <= low || root.val as i64 >= upper {
return false;
}
Self::valid_bst(low, root.val as i64, root.left.clone())
&& Self::valid_bst(root.val as i64, upper, root.right.clone())
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Auxiliary Array:
impl Solution {
pub fn is_valid_bst(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
let mut vec = vec![];
Self::valid_bst(root, &mut vec);
for i in 1..vec.len() {
if vec[i] <= vec[i - 1] {
return false;
}
}
true
}
pub fn valid_bst(root: Option<Rc<RefCell<TreeNode>>>, mut v: &mut Vec<i64>) {
if root.is_none() {
return;
}
let node = root.as_ref().unwrap().borrow();
Self::valid_bst(node.left.clone(), v);
v.push(node.val as i64);
Self::valid_bst(node.right.clone(), v);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C#
// Recursive
public long val = Int64.MinValue;
public bool IsValidBST(TreeNode root)
{
if (root == null) return true;
bool left = IsValidBST(root.left);
if (root.val > val) val = root.val;
else return false;
bool right = IsValidBST(root.right);
return left && right;
}
2
3
4
5
6
7
8
9
10
11
