# 59. Spiral Matrix II
LeetCode Problem Link (opens new window)
Given a positive integer n, generate an n x n matrix filled with elements from 1 to n^2 in a spiral order.
Example:
Input: 3
Output:
[
[ 1, 2, 3 ],
[ 8, 9, 4 ],
[ 7, 6, 5 ]
]
1
2
3
4
5
2
3
4
5
# Approach
This problem is frequently encountered in interviews and is essentially a simulation process rather than a complex algorithm. It tests one's ability to handle code effectively.
How can we draw a spiral matrix? Initially, many may find themselves overwhelmed with boundary conditions, but adhering to a systematic approach can make things easier. Remember the principle of loop invariants when tackling this.
Simulate the process of drawing the matrix in a clockwise spiral order:
- Fill the top row from left to right
- Fill the right column from top to bottom
- Fill the bottom row from right to left
- Fill the left column from bottom to top
Proceed layer by layer from the outermost towards the center.
Notice there are numerous boundary conditions. In a loop filled with such conditions, maintaining a consistent traversal rule is crucial. One should stick to either a closed-open or open-closed interval principle for each boundary.
Here's how we achieve it by applying a closed-open principle:
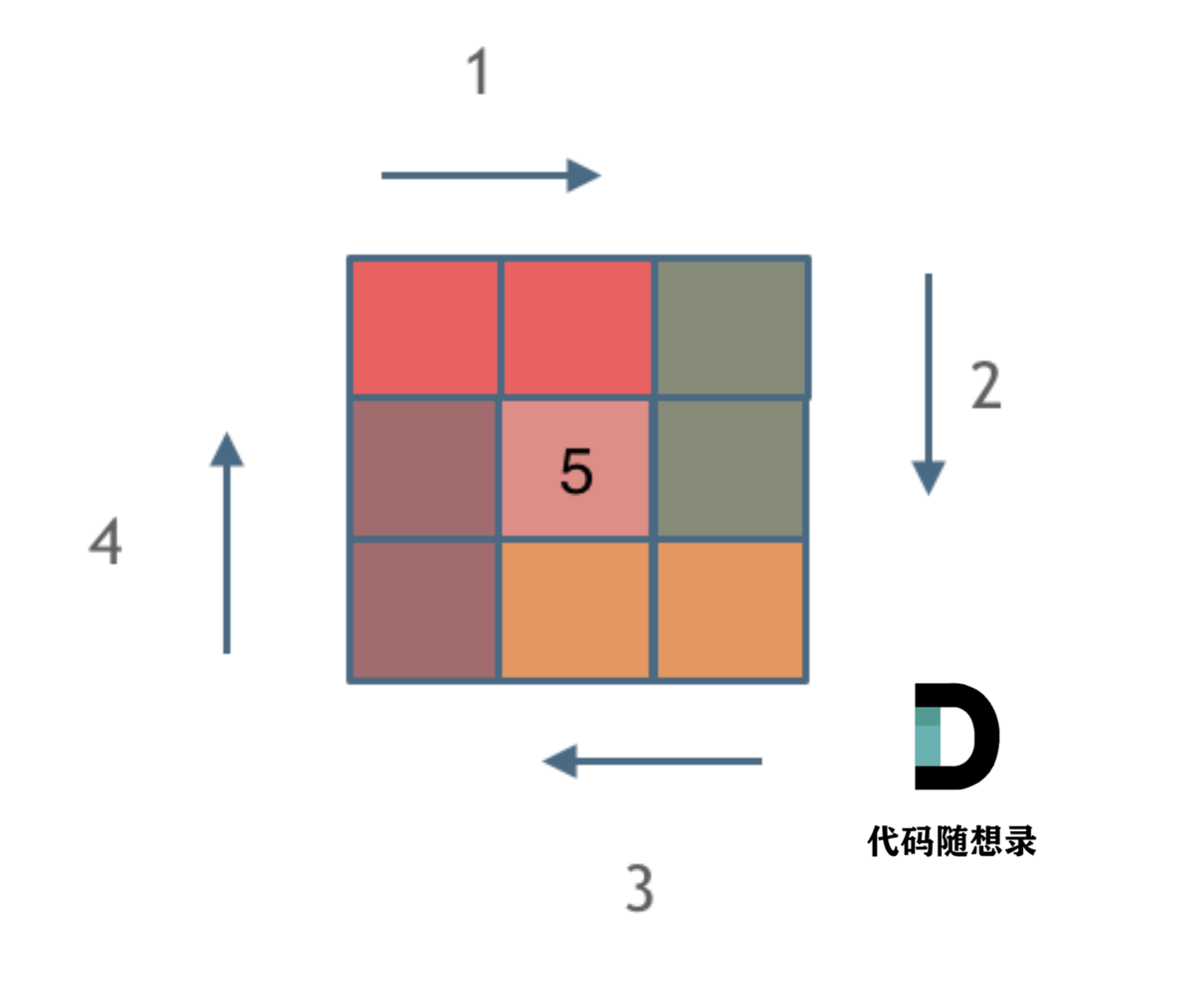
Here, each color represents a boundary, and you can notice how each corner follows a rule where the next boundary takes over to continue the process.
Once you resolve each corner consistently with the left-closed, right-open principle, the entire loop follows a smooth process.
Below is the C++ code for this problem with detailed comments explaining each step. Notice that the while loop has numerous checks, but the core principle of left-closed, right-open is consistent.
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0)); // Define a 2D vector
int startx = 0, starty = 0; // Starting position for each layer
int loop = n / 2; // Number of loops, e.g., for n=3, loop=1, only one loop needed, separate handling for the center
int mid = n / 2; // Middle position, for n=3, it's (1,1), for n=5, it's (2,2)
int count = 1; // Counter for filling numbers in the matrix
int offset = 1; // Control the traversal length of each boundary within a loop, shrink one boundary after each loop
int i,j;
while (loop --) {
i = startx;
j = starty;
// The following four loops simulate drawing one layer
// Fill the top row from left to right (left-closed, right-open)
for (j; j < n - offset; j++) {
res[i][j] = count++;
}
// Fill the right column from top to bottom (left-closed, right-open)
for (i; i < n - offset; i++) {
res[i][j] = count++;
}
// Fill the bottom row from right to left (left-closed, right-open)
for (; j > starty; j--) {
res[i][j] = count++;
}
// Fill the left column from bottom to top (left-closed, right-open)
for (; i > startx; i--) {
res[i][j] = count++;
}
// Move starting position to the inner layer, e.g., (0, 0) to (1, 1)
startx++;
starty++;
// Offset controls each boundary traversal length
offset += 1;
}
// If n is odd, handle center position separately
if (n % 2) {
res[mid][mid] = count;
}
return res;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
- Time Complexity: O(n^2): Simulating the traversal of a 2D matrix
- Space Complexity: O(1)
# Related Problems
# Other Language Versions
# Java:
class Solution {
public int[][] generateMatrix(int n) {
int[][] nums = new int[n][n];
int startX = 0, startY = 0; // The starting point for each layer
int offset = 1;
int count = 1; // The number to fill the matrix
int loop = 1; // Current loop index
int i, j; // j for columns, i for rows;
while (loop <= n / 2) {
// Top
// Close-open, so stop when j equals n - offset
for (j = startY; j < n - offset; j++) {
nums[startX][j] = count++;
}
// Right column
// Close-open, so stop when i equals n - offset
for (i = startX; i < n - offset; i++) {
nums[i][j] = count++;
}
// Bottom
// Close-open, stop when j equals startY
for (; j > startY; j--) {
nums[i][j] = count++;
}
// Left column
// Close-open, stop when i equals startX
for (; i > startX; i--) {
nums[i][j] = count++;
}
startX++;
startY++;
offset++;
loop++;
}
if (n % 2 == 1) { // For odd n, fill the center separately
nums[startX][startY] = count;
}
return nums;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Python3:
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
nums = [[0] * n for _ in range(n)]
startx, starty = 0, 0 # Start point
loop, mid = n // 2, n // 2 # Iteration count, mid point for odd n
count = 1 # Counter
for offset in range(1, loop + 1) : # Each loop increases offset, starting at 1
for i in range(starty, n - offset) : # From left to right, close-open
nums[startx][i] = count
count += 1
for i in range(startx, n - offset) : # From top to bottom
nums[i][n - offset] = count
count += 1
for i in range(n - offset, starty, -1) : # From right to left
nums[n - offset][i] = count
count += 1
for i in range(n - offset, startx, -1) : # From bottom to top
nums[i][starty] = count
count += 1
startx += 1 # Update start point
starty += 1
if n % 2 != 0 : # For odd n, handle center
nums[mid][mid] = count
return nums
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Version 2: Using four boundaries
class Solution(object):
def generateMatrix(self, n):
if n <= 0:
return []
# Initialize n x n matrix
matrix = [[0]*n for _ in range(n)]
# Initialize boundaries and starting number
top, bottom, left, right = 0, n-1, 0, n-1
num = 1
while top <= bottom and left <= right:
# Fill top boundary from left to right
for i in range(left, right + 1):
matrix[top][i] = num
num += 1
top += 1
# Fill right boundary from top to bottom
for i in range(top, bottom + 1):
matrix[i][right] = num
num += 1
right -= 1
# Fill bottom boundary from right to left
for i in range(right, left - 1, -1):
matrix[bottom][i] = num
num += 1
bottom -= 1
# Fill left boundary from bottom to top
for i in range(bottom, top - 1, -1):
matrix[i][left] = num
num += 1
left += 1
return matrix
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# JavaScript:
var generateMatrix = function(n) {
let startX = startY = 0; // Starting position
let loop = Math.floor(n/2); // Number of layers
let mid = Math.floor(n/2); // Mid point
let offset = 1; // Control the element number for each layer
let count = 1; // Update the fill number
let res = new Array(n).fill(0).map(() => new Array(n).fill(0));
while (loop--) {
let row = startX, col = startY;
// Top row traversal from left to right (closed-open)
for (; col < n - offset; col++) {
res[row][col] = count++;
}
// Right column traversal from top to bottom (closed-open)
for (; row < n - offset; row++) {
res[row][col] = count++;
}
// Bottom row traversal from right to left (closed-open)
for (; col > startY; col--) {
res[row][col] = count++;
}
// Left column traversal from bottom to top (closed-open)
for (; row > startX; row--) {
res[row][col] = count++;
}
// Update start position
startX++;
startY++;
// Update offset
offset += 1;
}
// For odd n, fill the center element
if (n % 2 === 1) {
res[mid][mid] = count;
}
return res;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# TypeScript:
function generateMatrix(n: number): number[][] {
let loopNum: number = Math.floor(n / 2);
const resArr: number[][] = new Array(n).fill(1).map(i => new Array(n));
let chunkNum: number = n - 1;
let startX: number = 0;
let startY: number = 0;
let value: number = 1;
let x: number, y: number;
while (loopNum--) {
x = startX;
y = startY;
while (x < startX + chunkNum) {
resArr[y][x] = value;
x++;
value++;
}
while (y < startY + chunkNum) {
resArr[y][x] = value;
y++;
value++;
}
while (x > startX) {
resArr[y][x] = value;
x--;
value++;
}
while (y > startY) {
resArr[y][x] = value;
y--;
value++;
}
startX++;
startY++;
chunkNum -= 2;
}
if (n % 2 === 1) {
resArr[startX][startY] = value;
}
return resArr;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Go:
package main
import "fmt"
func main() {
n := 3
fmt.Println(generateMatrix(n))
}
func generateMatrix(n int) [][]int {
startx, starty := 0, 0
var loop int = n / 2
var center int = n / 2
count := 1
offset := 1
res := make([][]int, n)
for i := 0; i < n; i++ {
res[i] = make([]int, n)
}
for loop > 0 {
i, j := startx, starty
// Not changing row count but changing column count
for j = starty; j < n-offset; j++ {
res[startx][j] = count
count++
}
// Not changing column count but changing row count
for i = startx; i < n-offset; i++ {
res[i][j] = count
count++
}
// Not changing row count but changing column count in reverse
for ; j > starty; j-- {
res[i][j] = count
count++
}
// Not changing column count but changing row count in reverse
for ; i > startx; i-- {
res[i][j] = count
count++
}
startx++
starty++
offset++
loop--
}
if n%2 == 1 {
res[center][center] = n * n
}
return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
func generateMatrix(n int) [][]int {
top, bottom := 0, n-1
left, right := 0, n-1
num := 1
tar := n * n
matrix := make([][]int, n)
for i := 0; i < n; i++ {
matrix[i] = make([]int, n)
}
for num <= tar {
for i := left; i <= right; i++ {
matrix[top][i] = num
num++
}
top++
for i := top; i <= bottom; i++ {
matrix[i][right] = num
num++
}
right--
for i := right; i >= left; i-- {
matrix[bottom][i] = num
num++
}
bottom--
for i := bottom; i >= top; i-- {
matrix[i][left] = num
num++
}
left++
}
return matrix
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Swift:
func generateMatrix(_ n: Int) -> [[Int]] {
var result = [[Int]](repeating: [Int](repeating: 0, count: n), count: n)
var startRow = 0
var startColumn = 0
var loopCount = n / 2
let mid = n / 2
var count = 1
var offset = 1
var row: Int
var column: Int
while loopCount > 0 {
row = startRow
column = startColumn
for c in column ..< startColumn + n - offset {
result[startRow][c] = count
count += 1
column += 1
}
for r in row ..< startRow + n - offset {
result[r][column] = count
count += 1
row += 1
}
for _ in startColumn ..< column {
result[row][column] = count
count += 1
column -= 1
}
for _ in startRow ..< row {
result[row][column] = count
count += 1
row -= 1
}
startRow += 1
startColumn += 1
offset += 2
loopCount -= 1
}
if (n % 2) != 0 {
result[mid][mid] = count
}
return result
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# Rust:
impl Solution {
pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
let mut res = vec![vec![0; n as usize]; n as usize];
let (mut startX, mut startY, mut offset): (usize, usize, usize) = (0, 0, 1);
let mut loopIdx = n/2;
let mid: usize = loopIdx as usize;
let mut count = 1;
let (mut i, mut j): (usize, usize) = (0, 0);
while loopIdx > 0 {
i = startX;
j = startY;
while j < (startY + (n as usize) - offset) {
res[i][j] = count;
count += 1;
j += 1;
}
while i < (startX + (n as usize) - offset) {
res[i][j] = count;
count += 1;
i += 1;
}
while j > startY {
res[i][j] = count;
count += 1;
j -= 1;
}
while i > startX {
res[i][j] = count;
count += 1;
i -= 1;
}
startX += 1;
startY += 1;
offset += 2;
loopIdx -= 1;
}
if(n % 2 == 1) {
res[mid][mid] = count;
}
res
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# PHP:
class Solution {
/**
* @param Integer $n
* @return Integer[][]
*/
function generateMatrix($n) {
// Initialize the result array size
*returnSize = n;
*returnColumnSizes = (int*)malloc(sizeof(int) * n);
// Initialize the result array ans
int** ans = (int**)malloc(sizeof(int*) * n);
int i;
for(i = 0; i < n; i++) {
ans[i] = (int*)malloc(sizeof(int) * n);
(*returnColumnSizes)[i] = n;
}
// Set the starting position for each loop
int startX = 0;
int startY = 0;
// Set the middle value of the 2D array, if n is odd, handle the center value separately
int mid = n / 2;
// Number of loops
int loop = n / 2;
// Offset
int offset = 1;
// Current element to be added
int count = 1;
while(loop > 0) {
int i = startX;
int j = startY;
// Simulate from left to right
for(; j < startY + n - offset; j++) {
ans[startX][j] = count++;
}
// Simulate from top to bottom
for(; i < startX + n - offset; i++) {
ans[i][j] = count++;
}
// Simulate from right to left
for(; j > startY; j--) {
ans[i][j] = count++;
}
// Simulate from bottom to top
for(; i > startX; i--) {
ans[i][j] = count++;
}
// Increase the offset by 2 each time
offset+=2;
// Traverse the start position is +1 each time
startX++;
startY++;
loop--;
}
// If n is odd, need to fill the center value separately
if(n % 2)
ans[mid][mid] = count;
return ans;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
# Scala:
object Solution {
def generateMatrix(n: Int): Array[Array[Int]] = {
var res = Array.ofDim[Int](n, n) // Define a n*n 2D matrix
var num = 1 // The current number to fill
var i = 0 // Horizontal coordinate
var j = 0 // Vertical coordinate
while (num <= n * n) {
// Fill from left to right: while j is in bounds and the next number is blank
while (j < n && res(i)(j) == 0) {
res(i)(j) = num // Current coordinate equals num
num += 1 // Increase num
j += 1 // Increase vertical coordinate
}
i += 1 // Move down a row
j -= 1 // Move left by a column
// Same for all remaining directions
// Fill from top to bottom
while (i < n && res(i)(j) == 0) {
res(i)(j) = num
num += 1
i += 1
}
i -= 1
j -= 1
// Fill from right to left
while (j >= 0 && res(i)(j) == 0) {
res(i)(j) = num
num += 1
j -= 1
}
i -= 1
j += 1
// Fill from bottom to top
while (i >= 0 && res(i)(j) == 0) {
res(i)(j) = num
num += 1
i -= 1
}
i += 1
j += 1
}
res
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# C#:
public int[][] GenerateMatrix(int n)
{
// Referencing Carl's Code Thoughts in C++
// https://www.programmercarl.com/0059.%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5II.html#%E6%80%9D%E8%B7%AF
int startX = 0, startY = 0; // Define starting position for each loop
int loop = n / 2; // Number of loops, e.g., n=3, loop=1, only one loop needed, handle center separately
int count = 1; // Counter to fill matrix
int mid = n / 2; // Middle position, e.g., for n=3, it's (1,1), for n=5, it's (2,2)
int offset = 1;// Control each loop's boundary traversal length
// Create result 2D array
int[][] result = new int[n][];
for (int k = 0; k < n; k++)
{
result[k] = new int[n];
}
int i = 0, j = 0; // [i,j]
while (loop > 0)
{
i = startX;
j = startY;
// Four for loops to simulate one layer
// First row traverse left to right, not including rightmost (closed-open)
for (; j < n - offset; j++)
{
result[i][j] = count++;
}
// Right column traverse top to bottom, not including bottommost (closed-open)
for (; i < n - offset; i++)
{
result[i][j] = count++;
}
// Bottom row traverse right to left, not including leftmost (closed-open)
for (; j > startY; j--)
{
result[i][j] = count++;
}
// Left column traverse bottom to top, not including topmost (closed-open)
for (; i > startX; i--)
{
result[i][j] = count++;
}
// Move starting position for each subsequent layer, e.g., (0, 0) to (1, 1)
startX++;
startY++;
// Offset adjusts each boundary traversal length
offset++;
loop--;
}
if (n % 2 == 1)
{
// If n is odd
result[mid][mid] = count;
}
return result;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# Ruby:
def generate_matrix(n)
result = Array.new(n) { Array.new(n, 0) }
# Number of loops
loop_times = 0
# Offset
step = n - 1
val = 1
while loop_times < n / 2
# Simulate left to right
for i in 0..step - 1
# Row constant, column changes
result[loop_times][i+loop_times] = val
val += 1
end
# Simulate top to bottom
for i in 0..step - 1
# Column constant, row changes
result[i+loop_times][n-loop_times-1] = val
val += 1
end
# Simulate right to left
for i in 0..step - 1
# Row constant, column changes
result[n-loop_times-1][n-loop_times-i-1] = val
val += 1
end
# Simulate bottom to top
for i in 0..step - 1
# Column constant, row changes
result[n-loop_times-i-1][loop_times] = val
val += 1
end
loop_times += 1
step -= 2
end
# If odd number, fill the center element
result[n/2][n/2] = n**2 if n % 2
return result
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
Copyright © 2025 keetcoder