35. Search Insert Position

LeetCode Problem Link (opens new window)

Given a sorted array and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You may assume no duplicates in the array.

Example 1:

• Input: [1,3,5,6], 5
• Output: 2

Example 2:

• Input: [1,3,5,6], 2
• Output: 1

Example 3:

• Input: [1,3,5,6], 7
• Output: 4

Example 4:

• Input: [1,3,5,6], 0
• Output: 0

Approach

This problem is not difficult, but the relatively low acceptance rate may be due to misjudgments in handling borders.

To insert a target value into an array, there can be four situations:

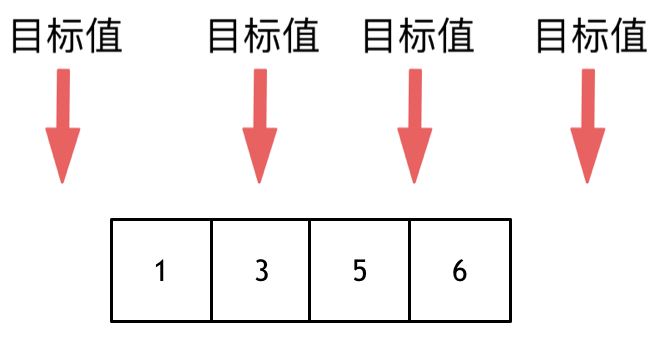
• The target value is before all elements of the array.
• The target value equals one of the elements of the array.
• The target value fits into the position among the sorted elements.
• The target value is after all elements of the array.

Once these four situations are clear, you can attempt to solve the problem.

I'll explain this problem using both a brute force method and the binary search method, and take this opportunity to elaborate on the binary search method.

Brute Force Approach

A brute force solution doesn’t necessarily mean it is very time-consuming. The key is in the implementation method, just as a binary search isn’t always time-efficient.

C++ Code

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        for (int i = 0; i < nums.size(); i++) {
        // Handle the following three cases respectively
        // The target value is before all elements
        // The target value equals one of the array's elements
        // The target value fits into the position among sorted elements
            if (nums[i] >= target) { // Once a number greater than or equal to the target is found, i is the result we want
                return i;
            }
        }
        // The case where the target value is after all elements of the array
        return nums.size(); // If the target is the largest, or if nums is empty, it returns the length of nums
    }
};

• Time complexity: O(n)
• Space complexity: O(1)

Efficiency is as follows:

Binary Search Approach

Given that the brute force method’s time complexity is O(n), let's try using binary search.

Notice that the given array is sorted, which is the fundamental condition for using binary search.

In interview questions, whenever a sorted array is presented, consider whether binary search can be applied.

Moreover, the problem states there are no duplicate elements in the array, as the index of elements found by binary search might not be unique if there were duplicates.

Let’s generally explain the idea of binary search with an example, such as finding the element 5 in this array and returning its index.

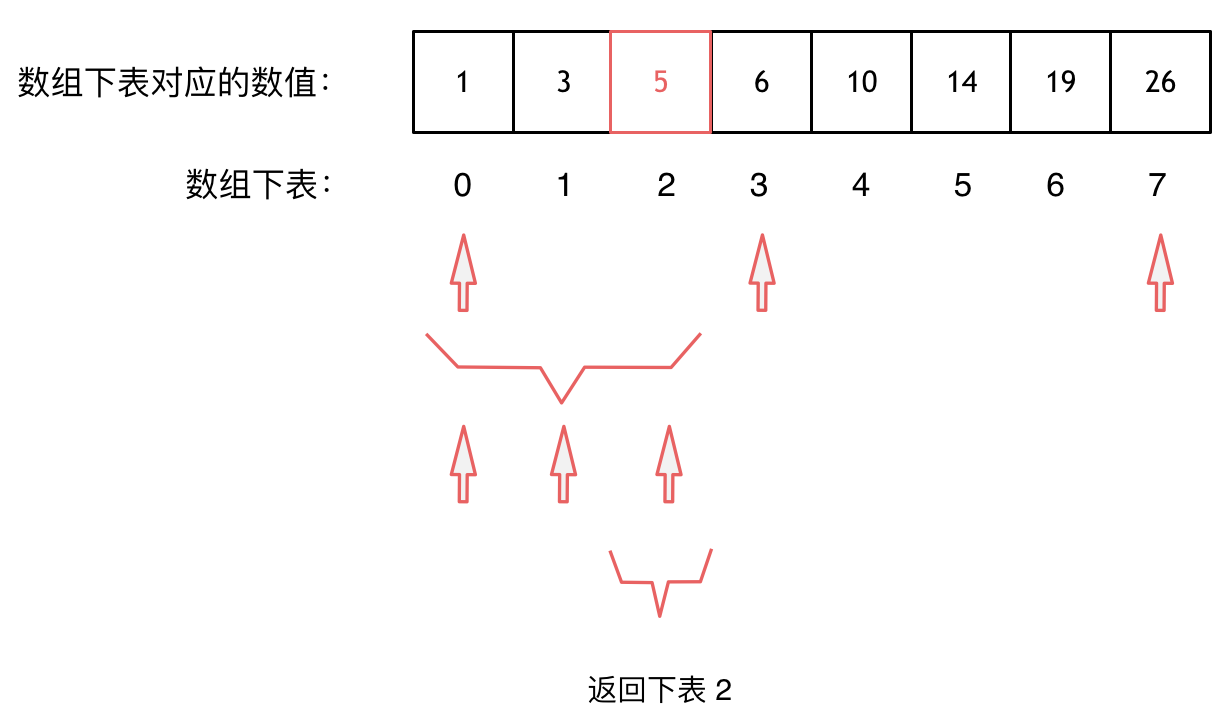
Binary search involves many boundary conditions, the logic is simple but writing it correctly is challenging.

Many find it difficult to handle boundary conditions in binary search.

For example, whether to write while(left < right) or while(left <= right), or whether to write right = middle or right = middle - 1.

The confusion mainly arises depending on how you define the scope of the interval, which is the invariant.

The purpose is to maintain the invariant in the binary search process, which is a loop invariant (feel free to explore more about this concept).

First Binary Search Method

Take this problem as an example, the following code defines target in the closed interval on both ends, i.e., [left, right] (this is important).

This decides how to write the binary search code, please check the code below:

Note the comments carefully and think about why it’s written as while(left <= right), and why it’s written as right = middle - 1.

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n - 1; // Define the target within a closed interval [left, right]
        while (left <= right) { // When left==right, the interval [left, right] is still valid
            int middle = left + ((right - left) / 2); // Prevent overflow, equivalent to (left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target is in the left interval, so [left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target is in the right interval, so [middle + 1, right]
            } else { // nums[middle] == target
                return middle;
            }
        }
        // Handle the following four cases respectively
        // Target value is before all elements [0, -1]
        // Target equals one of the elements, return middle;
        // Target fits into the array [left, right], return right + 1
        // Target is after all elements [left, right], since it's a closed interval, return right + 1
        return right + 1;
    }
};

• Time complexity: O(log n)
• Space complexity: O(1)

Efficiency is as follows:

Second Binary Search Method

If defining target as within a left-closed, right-open interval, i.e., [left, right).

Then the handling method for the binary search boundaries differs entirely.

The invariant is [left, right) interval, you can see how the code insists on the invariant in the loop.

Pay close attention to the comments and think about why it's written as while (left < right), and why right = middle.

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n; // Define the target in a left-closed, right-open interval [left, right)
        while (left < right) { // Because when left == right, [left, right) is an invalid range
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target is in the left interval, i.e., [left, middle)
            } else if (nums[middle] < target) {
                left = middle + 1; // target is in the right interval, i.e., [middle+1, right)
            } else { // nums[middle] == target
                return middle; // Found target in array, return index
            }
        }
        // Handle the following four cases:
        // Target value is before all elements [0,0)
        // Target equals one of the elements, return middle
        // Target fits into the array [left, right), return right
        // Target is after all elements [left, right), since it's a right-open interval, return right
        return right;
    }
};

• Time complexity: O(log n)
• Space complexity: O(1)

Summary

Through this task, I hope you understand why binary search is hard to write correctly, mainly due to an unclear definition of the interval.

Determine whether the search interval is left-closed, right-open [left, right), or left-closed, right-closed [left, right], which is the invariant.

Then, adhere to the principle of loop invariants throughout the binary search, and many detailed issues will naturally become clear on how to handle them.

Other Language Versions

Java

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;

        // Define target in a closed interval [low, high]
        int low = 0;
        int high = n - 1;

        while (low <= high) { // When low==high, the interval [low, high] is still valid
            int mid = low + (high - low) / 2; // Prevent overflow
            if (nums[mid] > target) {
                high = mid - 1; // target is in the left interval, so [low, mid - 1]
            } else if (nums[mid] < target) {
                low = mid + 1; // target is in the right interval, so [mid + 1, high]
            } else {
                // 1. Target equals one of the elements, return mid;
                return mid;
            }
        }
        // 2. Target is before all elements, 3. Fits into the array, 4. Target is after all elements, return right + 1;
        return high + 1;
    }
}

// Second binary search method: left-closed, right-open
public int searchInsert(int[] nums, int target) {
    int left = 0;
    int right = nums.length;
    while (left < right) { // Left-closed, right-open [left, right)
        int middle = left + ((right - left) >> 1);
        if (nums[middle] > target) {
            right = middle; // target is in the left interval, i.e., [left, middle)
        } else if (nums[middle] < target) {
            left = middle + 1; // target is in the right interval, i.e., [middle+1, right)
        } else { // nums[middle] == target
            return middle; // Found target in array, return index
        }
    }
    // Target is before all elements [0,0)
    // Fits into the array [left, right), return right
    // Target is after all elements [left, right), since it's a right-open interval, return right
    return right;
}

C#

public int SearchInsert(int[] nums, int target) {
	
	var left = 0;
	var right = nums.Length - 1;

	while (left <= right) {
		
		var curr = (left + right) / 2;
		
		if (nums[curr] == target)
		{
			return curr;	
		}
		
		if (target > nums[curr]) {
			left = curr + 1;
		}
		else {
			right = curr - 1;
		}
	}
	
	return left;
}

Golang

// First binary search method
func searchInsert(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left <= right {
		mid := left + (right-left)/2
		if nums[mid] == target {
			return mid
		} else if nums[mid] > target {
			right = mid - 1
		} else {
			left = mid + 1
		}
	}
	return right+1
}

Rust

impl Solution {
      pub fn search_insert(nums: Vec<i32>, target: i32) -> i32 {
        use std::cmp::Ordering::{Equal, Greater, Less};
        let (mut left, mut right) = (0, nums.len() as i32 - 1);
        while left <= right {
            let mid = (left + right) / 2;
            match nums[mid as usize].cmp(&target) {
                Less => left = mid + 1,
                Equal => return mid,
                Greater => right = mid - 1,
            }
        }
        right + 1
    }
}

Python

# First binary search method: [left, right] closed interval
class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1

        while left <= right:
            middle = (left + right) // 2

            if nums[middle] < target:
                left = middle + 1
            elif nums[middle] > target:
                right = middle - 1
            else:
                return middle
        return right + 1

# Second binary search method: [left, right) left-closed right-open interval
class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums)

        while (left < right):
            middle = (left + right) // 2

            if nums[middle] > target:
                right = middle
            elif nums[middle] < target:
                left = middle + 1
            else:
                return middle

        return right

JavaScript

var searchInsert = function (nums, target) {
  let l = 0, r = nums.length - 1, ans = nums.length;

  while (l <= r) {
    const mid = l + Math.floor((r - l) >> 1);

    if (target > nums[mid]) {
      l = mid + 1;
    } else {
      ans = mid;
      r = mid - 1;
    }
  }

  return ans;
};

TypeScript

// First binary search method
function searchInsert(nums: number[], target: number): number {
    const length: number = nums.length;
    let left: number = 0,
        right: number = length - 1;
    while (left <= right) {
        const mid: number = Math.floor((left + right) / 2);
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] === target) {
            return mid;
        } else {
            right = mid - 1;
        }
    }
    return right + 1;
};

Swift

// Brute force method
func searchInsert(_ nums: [Int], _ target: Int) -> Int {
    for i in 0..<nums.count {
        if nums[i] >= target {
            return i
        }
    }
    return nums.count
}

// Binary search
func searchInsert(_ nums: [Int], _ target: Int) -> Int {
    var left = 0
    var right = nums.count - 1

    while left <= right {
        let middle = left + ((right - left) >> 1)

        if nums[middle] > target {
            right = middle - 1
        }else if nums[middle] < target {
            left = middle + 1
        }else if nums[middle] == target {
            return middle
        }
    }

    return right + 1
}

Scala

object Solution {
  def searchInsert(nums: Array[Int], target: Int): Int = {
    var left = 0
    var right = nums.length - 1
    while (left <= right) {
      var mid = left + (right - left) / 2
      if (target == nums(mid)) {
        return mid
      } else if (target > nums(mid)) {
        left = mid + 1
      } else {
        right = mid - 1
      }
    }
    right + 1
  }
}

PHP

// Binary search (1): [left, right] closed interval
function searchInsert($nums, $target)
{
    $n = count($nums);
    $l = 0;
    $r = $n - 1;
    while ($l <= $r) {
        $mid = floor(($l + $r) / 2);
        if ($nums[$mid] > $target) {
            // Next search in the left interval: [$l,$mid-1]
            $r = $mid - 1;
        } else if ($nums[$mid] < $target) {
			// Next search in the right interval: [$mid+1,$r]
			$l = $mid + 1;
		} else {
			// Found, return
			return $mid;
		}
    }
    return $r + 1;
}

C

// Version one [left, right] closed interval
int searchInsert(int* nums, int numsSize, int target){
    // Left closed, right open interval [0 , numsSize-1]
        int left =0;
        int mid =0;
        int right = numsSize - 1;
        while(left <= right){// Closed interval so left == right
            mid = left + (right - left) / 2;
            if(target < nums[mid]){
        // target is in the interval [left, mid - 1], original range includes mid, right boundary can be narrowed
                right = mid -1;
            }else if( target > nums[mid]){
        // target is in the interval [mid + 1, right], original range includes mid, left boundary can be narrowed
                left = mid + 1;
            }else {
        // nums[mid] == target, found target, return mid
                return mid;
            }
        }
        // Target not found in the array
        // Target is after all elements, [left, right] is closed, so return right +1
        return right + 1;
}

// Version two [left, right] open interval
int searchInsert(int* nums, int numsSize, int target){
    // Left closed, right open interval [0 , numsSize)
        int left =0;
        int mid =0;
        int right = numsSize;
        while(left < right){// Open interval so left < right
            mid = left + (right - left) / 2;
            if(target < nums[mid]){
        // target is in the interval [left, mid), original range doesn't include mid, so right boundary can't be narrowed
                right = mid ;
            }else if( target > nums[mid]){
        // target is in the interval [mid+1, right), original range includes mid, so left boundary can be narrowed
                left = mid + 1;
            }else {
        // nums[mid] == target, found target, return mid
                return mid;
            }
        }
	// Target not found in the array
        // Target is after all elements, [left, right) is open, so return right
        return right;
}