Can this also be solved by the backtracking method? In fact, DFS and backtracking complement each other since both use recursion.

332. Reconstruct Itinerary

LeetCode Problem Link (opens new window)

Given a list of airline tickets represented as a 2D string array [from, to], where each pair [from, to] indicates a ticket from city from to city to, reconstruct the itinerary in order. All tickets belong to a man who departs from JFK, thus the itinerary must begin with JFK.

Hints:

• If there are multiple valid itineraries, return the itinerary that has the smallest lexical order when read as a single string. For example, ["JFK", "LGA"] is smaller than ["JFK", "LGB"].
• All airports are represented by three capital letters (airport code).
• You may assume all tickets form at least one valid itinerary.
• You must use all the tickets once and only once.

Example 1:

• Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
• Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]

Example 2:

• Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
• Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
• Explanation: Another valid itinerary is ["JFK","SFO","ATL","JFK","ATL","SFO"]. However, it is larger in lexical order.

Strategy

This is a complex problem. Previously, we've used the backtracking approach to solve problems like 0077.Combinations (opens new window), 0093.Restore IP Addresses (opens new window), 0078.Subsets (opens new window), and 0046.Permutations (opens new window).

At first glance, this problem seems unrelated to backtracking and more like a depth-first search (DFS) in graph theory. Indeed, it is DFS; however, this is an example of using backtracking in DFS. In the process of finding a path, if you don't backtrack, how can you reach the target path?

Therefore, I would say this problem should be solved using backtracking. I will explain this problem using the backtracking approach. In reality, DFS generally utilizes the backtracking technique, which I will elaborate on in detail in my graph theory series.

This is a demonstration of how versatile backtracking can be!

This problem presents several challenges:

1. In an itinerary, it is easy to form a loop if flights are not properly handled, leading to deadlock.
2. There are multiple valid solutions, and the itinerary must be lexically smallest. How should we record the mapping relationship?
3. When using backtracking (or DFS), what is the termination condition?
4. During the search process, how to traverse all the airports from one airport?

I'll answer these questions one by one!

Understanding Loops

Regarding deadlocks, let me give an example with repeated airports:

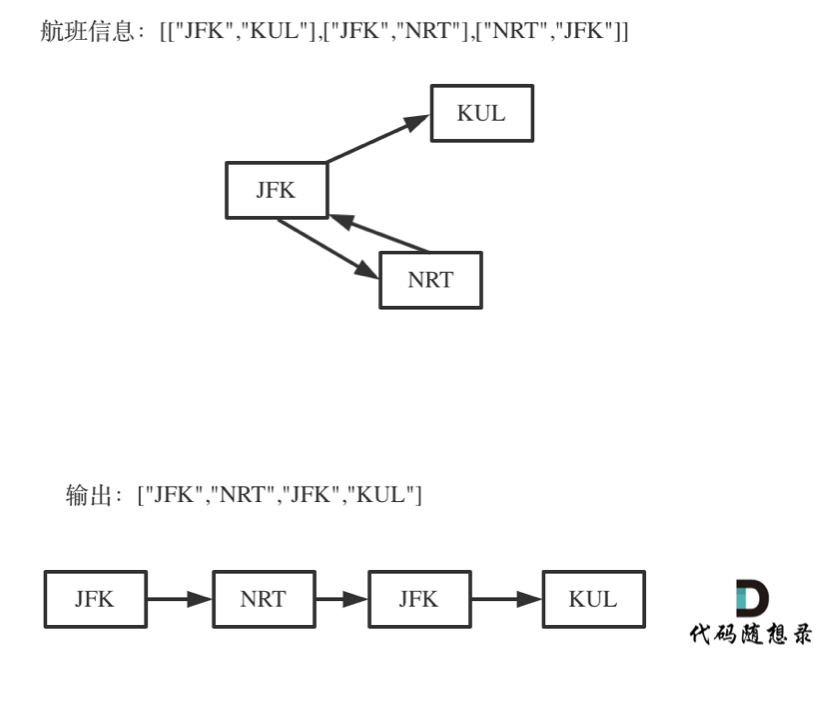
Why give this example? It's to show that both the departure and destination airports can repeat. If you don't handle the elements in the set correctly, you'll end up in an infinite loop.

Recording Mapping Relationships

With multiple solutions, and needing itineraries sorted alphabetically, many find this aspect daunting. How can one record the mapping relationship?

A single airport maps to multiple airports, and destinations should be sorted alphabetically. We can use std::unordered_map for a single airport mapping multiple airports. If the destinations need to be in order, we can use std::map, std::multimap, or std::multiset.

If you're unsure about the implementation of map and set, or why map and multimap are sorted, you can read this article: Hash Table Basics (opens new window).

Storing mapping relationships can be defined as unordered_map<string, multiset<string>> targets or unordered_map<string, map<string, int>> targets.

Here are their meanings:

unordered_map<string, multiset<string>> targets: unordered_map<departure airport, set of destination airports> targets

unordered_map<string, map<string, int>> targets: unordered_map<departure airport, map<destination airport, flight count>> targets

I chose the latter because using unordered_map<string, multiset<string>> targets, you cannot delete elements while iterating through the multiset, as the iterator will become invalid.

So, why must we add and remove elements? As shown in the diagram at the beginning, departure and destination airports may repeat. Without timely removing the destination airports during the search process, you may end up in an infinite loop.

So during the search process, I continually delete elements from the multiset. Hence, I recommend using unordered_map<string, map<string, int>> targets.

Within the traversal of unordered_map<departure airport, map<destination airport, flight count>> targets, the "flight count" can be used to mark whether the destination airport has been used.

If the "flight count" is greater than zero, the destination is still reachable. If it's zero, the destination is no longer reachable, thus eliminating the need to directly add or remove elements from the set.

In essence, instead of deleting, I just make a mark!

Backtracking

For this problem, I'm using the backtracking method. Let's approach it with my backtracking template:

void backtracking(parameters) {
    if (termination condition) {
        store result;
        return;
    }

    for (choices: elements in the current level collection (the number of child nodes in the tree is the size of the collection)) {
        process the node;
        backtracking(path, choices list); // recursion
        undo the process, backtrack
    }
}

Taking the input [["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]] as an example, it can be abstracted into the following tree structure:

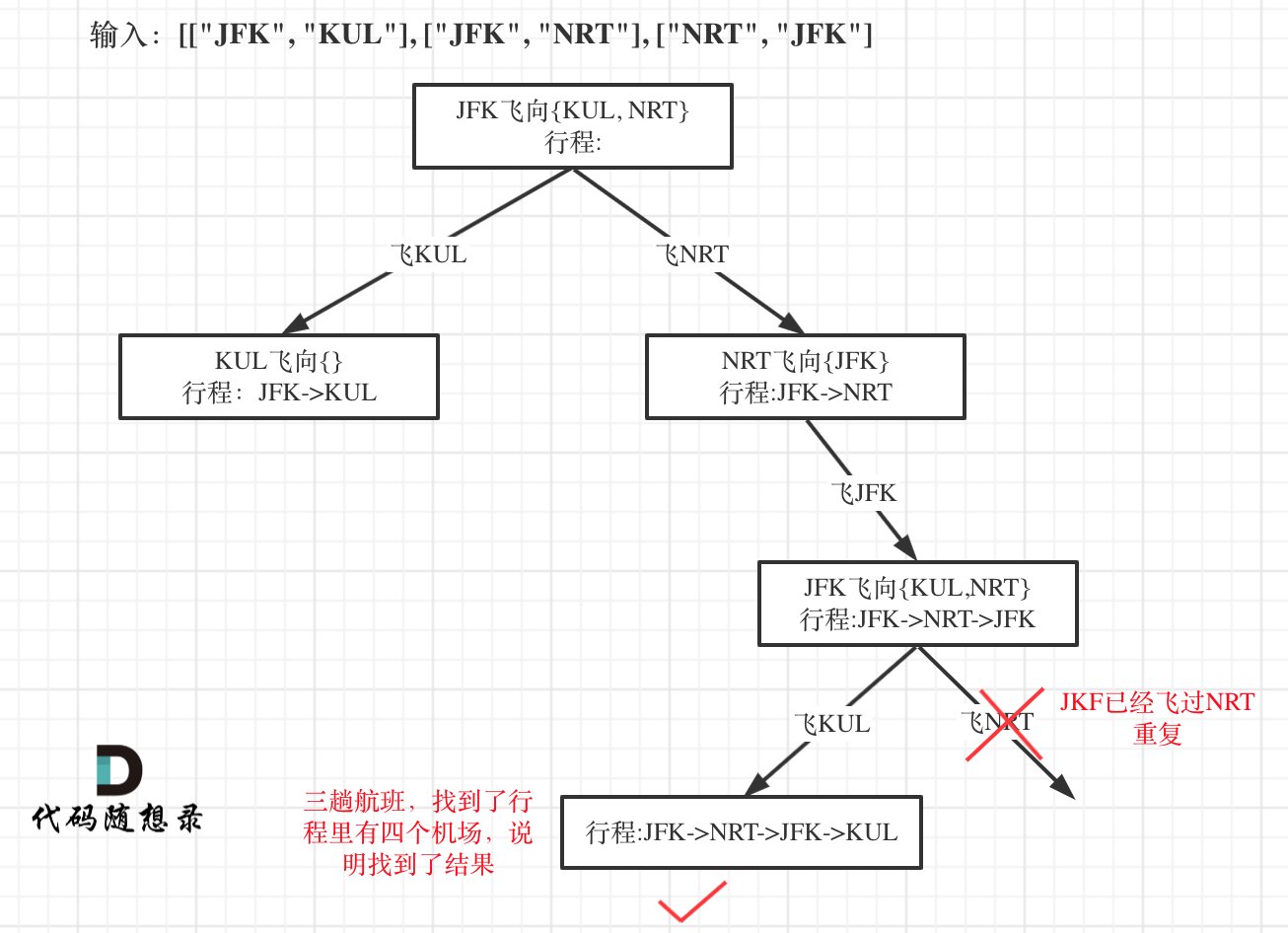
Let's proceed with the three-step explanation for backtracking:

• Recursive Function Parameters

When explaining mapping relationships, we've already covered using unordered_map<string, map<string, int>> targets; for recording flight mapping relationships, which I've defined as a global variable.

Of course, including the parameters in the function is also possible, but I aim to keep the function parameter length controlled.

Within the parameters, you'll also need ticketNum, representing the number of flights (used in the termination condition).

Here's the code:

// unordered_map<departure airport, map<destination airport, flight count>> targets
unordered_map<string, map<string, int>> targets;
bool backtracking(int ticketNum, vector<string>& result) {

Note that I've used bool as the function's return type!

When explaining the backtracking algorithm, the function return value is typically void. Why is it bool this time?

Because we only need to find a single itinerary, it's essentially finding the only path leading to a leaf node in the tree structure, as shown:

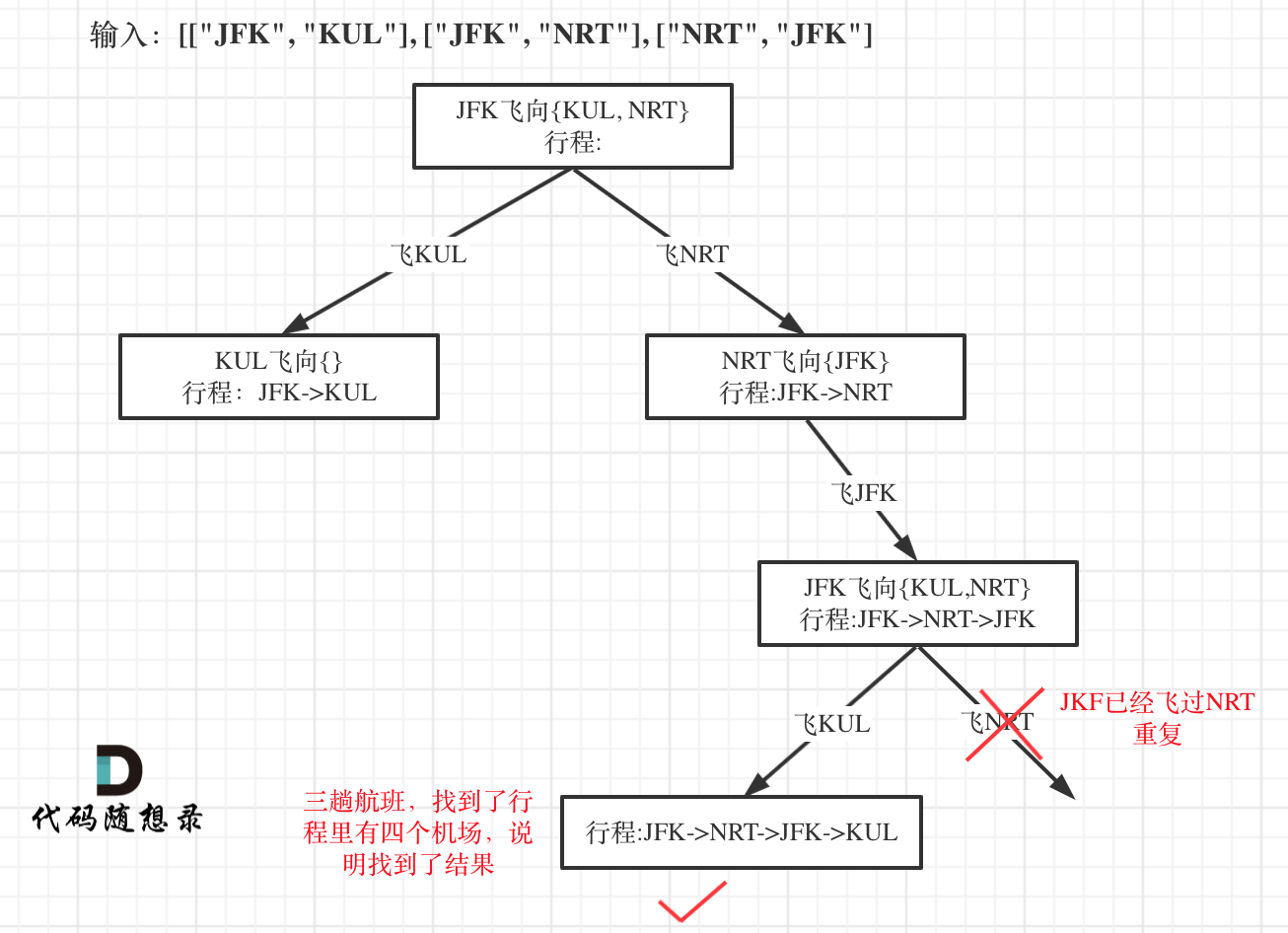
So once you've found this leaf node, you can return immediately. The function's return value issue was covered extensively in our binary tree series, particularly in this article: 0112.Path Sum (opens new window).

Of course, the targets and result need initialization, as shown:

for (const vector<string>& vec : tickets) {
    targets[vec[0]][vec[1]]++; // Record mapping relationships
}
result.push_back("JFK"); // Starting airport

• Termination Condition

Using the problem's example, with input [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]], there are 4 flights. Thus, to find a complete itinerary, the number of airports in the itinerary should be 5.

Therefore, the termination condition is: during our backtracking traversal, if the number of airports encountered matches (number of flights + 1), we have found a complete itinerary.

Here's the implementation:

if (result.size() == ticketNum + 1) {
    return true;
}

Reviewing backtracking code, upon reaching a leaf node, you might instinctively think to collect the result. However, it isn't necessary here; result in this problem acts similarly to path in 0216.Combination Sum III (opens new window), essentially recording the path (just one). In the single-layer search logic below, result already adds elements.

• Single Layer Search Logic

During backtracking, how should one traverse all airports corresponding to one airport?

Mentioned earlier, when selecting a mapping function, don't choose unordered_map<string, multiset<string>> targets, because if an element is added or removed, the multiset iterator will become invalid. This isn't the place to discuss containers where the iterator doesn't become invalid upon deletion.

For this problem, you need a container that orders data and allows easy adding/removal of elements without invalidating the iterator.

That's why I chose unordered_map<string, map<string, int>> targets for airport mapping.

The traversal process is as follows:

for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
    if (target.second > 0 ) { // Mark whether the destination airport has been used
        result.push_back(target.first);
        target.second--;
        if (backtracking(ticketNum, result)) return true;
        result.pop_back();
        target.second++;
    }
}

It's clear here that the int field in unordered_map<string, map<string, int>> targets indicates whether an airport in the set has been used, thereby avoiding the need to directly remove elements.

After this analysis, the complete C++ code is:

class Solution {
private:
// unordered_map<departure airport, map<destination airport, flight count>> targets
unordered_map<string, map<string, int>> targets;
bool backtracking(int ticketNum, vector<string>& result) {
    if (result.size() == ticketNum + 1) {
        return true;
    }
    for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
        if (target.second > 0 ) { // Mark whether the destination airport has been used
            result.push_back(target.first);
            target.second--;
            if (backtracking(ticketNum, result)) return true;
            result.pop_back();
            target.second++;
        }
    }
    return false;
}
public:
    vector<string> findItinerary(vector<vector<string>>& tickets) {
        targets.clear();
        vector<string> result;
        for (const vector<string>& vec : tickets) {
            targets[vec[0]][vec[1]]++; // Record mapping relationships
        }
        result.push_back("JFK"); // Starting airport
        backtracking(tickets.size(), result);
        return result;
    }
};

After thorough analysis, we see that the approach follows the backtracking algorithm template.

In the code:

for (pair<const string, int>& target : targets[result[result.size() - 1]])

You must add a reference, i.e., & target, because later on, there's an operation on target.second that decrements it. Without the reference, it would simply copy, and that result wouldn't be recorded, causing the final result to be incorrect.

Once you add a reference, you must add const before string due to syntax requirements since a map key is immutable.

Summary

This problem can indeed be considered a hard-level problem. The challenges I've mentioned are outlined in the text.

Solving this problem using a simple backtracking search (DFS) isn't challenging; the difficulty lies in choosing and using the right container.

It can be considered a deep depth-first search problem, but I've explained it entirely through the lens of backtracking, offering an expansion of thought and illustrating how inseparable DFS and backtracking really are since both ultimately use recursion.

While you may find that you can draw the final code following the backtracking template, the difficulty lies in recognizing backtracking's applicability and fitting it into the solution, which is why I've provided such an extensive and detailed explanation.

Other Language Versions

Java

class Solution {
    private LinkedList<String> res;
    private LinkedList<String> path = new LinkedList<>();

    public List<String> findItinerary(List<List<String>> tickets) {
        Collections.sort(tickets, (a, b) -> a.get(1).compareTo(b.get(1)));
        path.add("JFK");
        boolean[] used = new boolean[tickets.size()];
        backTracking((ArrayList) tickets, used);
        return res;
    }

    public boolean backTracking(ArrayList<List<String>> tickets, boolean[] used) {
        if (path.size() == tickets.size() + 1) {
            res = new LinkedList(path);
            return true;
        }

        for (int i = 0; i < tickets.size(); i++) {
            if (!used[i] && tickets.get(i).get(0).equals(path.getLast())) {
                path.add(tickets.get(i).get(1));
                used[i] = true;

                if (backTracking(tickets, used)) {
                    return true;
                }

                used[i] = false;
                path.removeLast();
            }
        }
        return false;
    }
}

class Solution {
    private Deque<String> res;
    private Map<String, Map<String, Integer>> map;

    private boolean backTracking(int ticketNum){
        if(res.size() == ticketNum + 1){
            return true;
        }
        String last = res.getLast();
        if(map.containsKey(last)){// To prevent null
            for(Map.Entry<String, Integer> target : map.get(last).entrySet()){
                int count = target.getValue();
                if(count > 0){
                    res.add(target.getKey());
                    target.setValue(count - 1);
                    if(backTracking(ticketNum)) return true;
                    res.removeLast();
                    target.setValue(count);
                }
            }
        }
        return false;
    }

    public List<String> findItinerary(List<List<String>> tickets) {
        map = new HashMap<String, Map<String, Integer>>();
        res = new LinkedList<>();
        for(List<String> t : tickets){
            Map<String, Integer> temp;
            if(map.containsKey(t.get(0))){
                temp = map.get(t.get(0));
                temp.put(t.get(1), temp.getOrDefault(t.get(1), 0) + 1);
            }else{
                temp = new TreeMap<>();// Ascending order Map
                temp.put(t.get(1), 1);
            }
            map.put(t.get(0), temp);

        }
        res.add("JFK");
        backTracking(tickets.size());
        return new ArrayList<>(res);
    }
}

/*  This method is an improvement over the second method. The main improvement is to transform the destinations of a point into a linked list format. The advantages are:
    1. Adding destinations is directly done at the corresponding position, avoiding frequent adjustments during the addition of elements in TreeMap.
    2. Meanwhile, each time you add, delete, or search for a destination, you operate with subscripts, avoiding repeated hash calculations in hashMap.
 */
class Solution {
    private Map<String, LinkedList<String>> ticketMap = new HashMap<>();
    private LinkedList<String> result = new LinkedList<>();
    private int total;

    public List<String> findItinerary(List<List<String>> tickets) {
        total = tickets.size() + 1;
        // Traverse the tickets and store in ticketMap
        for (List<String> ticket : tickets) {
            addNew(ticket.get(0), ticket.get(1));
        }
        deal("JFK");
        return result;
    }

    boolean deal(String currentLocation) {
        result.add(currentLocation);
        // If all tickets are used up, we've found the smallest lexical order path
        if (result.size() == total) {
            return true;
        }
        // Destination list of the current location
        LinkedList<String> targetLocations = ticketMap.get(currentLocation);
        // If there are no flights from this location, this path is not feasible
        if (targetLocations != null && !targetLocations.isEmpty()) {
            // Iterate through tickets departing from the current location
            for (int i = 0; i < targetLocations.size(); i++) {
                // To avoid repetitions. Otherwise, in the final test case, infinite recursion occurs when encountering loops
                if(i > 0 && targetLocations.get(i).equals(targetLocations.get(i - 1))) continue;
                String targetLocation = targetLocations.get(i);
                // Delete the current destination from the destination list
                targetLocations.remove(i);
                // Recurse
                if (deal(targetLocation)) {
                    return true;
                }
                // The path is not feasible, add the ticket back
                targetLocations.add(i, targetLocation);
                result.removeLast();
            }
        }
        return false;
    }
...

For the sake of length, I show a snapshot of Java 3rd implementation. Let me know if you want the rest.

Python

Backtracking using dictionaries:

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        self.adj = {}

        # sort by the destination alphabetically
        # Sort the destination of each flight alphabetically
        tickets.sort(key=lambda x:x[1])

        # get all possible connection for each destination
        # Entire next options of each station
        for u,v in tickets:
            if u in self.adj: self.adj[u].append(v)
            else: self.adj[u] = [v]

        # Start from JFK
        self.result = []
        self.dfs("JFK")  # start with JFK

        return self.result[::-1]  # Reverse to get the correct result

    def dfs(self, s):
        # If there is a flight for the departure city and the flight can go to another city
        while s in self.adj and len(self.adj[s]) > 0:
            # Find where s can go, choose the first airport
            v = self.adj[s][0]  # Go to 1 choice of the city
            # Remove this airport among the following options
            self.adj[s].pop(0)  # Get rid of this choice since used
            # Start from the new starting point
            self.dfs(v)  # Start from the new airport

        self.result.append(s)  # After appending, it will backtrack to last node, the result list is in reversed order

Backtracking using dictionary reverse order:

from collections import defaultdict

class Solution:
    def findItinerary(self, tickets):
        targets = defaultdict(list)  # Create default dictionary to store airport mappings
        for ticket in tickets:
            targets[ticket[0]].append(ticket[1])  # Add the ticket to the dictionary
        
        for key in targets:
            targets[key].sort(reverse=True)  # Sort the destination list in reverse order
        
        result = []
        self.backtracking("JFK", targets, result)  # Call backtracking function to start searching for the path
        return result[::-1]  # Return the reverse of the itinerary
        
    def backtracking(self, airport, targets, result):
        while targets[airport]:  # While there are destinations for the airport
            next_airport = targets[airport].pop()  # Pop the next airport
            self.backtracking(next_airport, targets, result)  # Recurse using DFS for the next airport
        result.append(airport)  # Add the current airport to the itinerary path

Go

type pair struct {
	target  string
	visited bool
}
type pairs []*pair

func (p pairs) Len() int {
	return len(p)
}
func (p pairs) Swap(i, j int) {
	p[i], p[j] = p[j], p[i]
}
func (p pairs) Less(i, j int) bool {
	return p[i].target < p[j].target
}

func findItinerary(tickets [][]string) []string {
	result := []string{}
	// map[departure airport] pair{destination airport, visited}
	targets := make(map[string]pairs)
	for _, ticket := range tickets {
		if targets[ticket[0]] == nil {
			targets[ticket[0]] = make(pairs, 0)
		}
		targets[ticket[0]] = append(targets[ticket[0]], &pair{target: ticket[1], visited: false})
	}
	for k, _ := range targets {
		sort.Sort(targets[k])
	}
	result = append(result, "JFK")
	var backtracking func() bool
	backtracking = func() bool {
		if len(tickets)+1 == len(result) {
			return true
		}
		// Fetch next destinations from the current airport
		for _, pair := range targets[result[len(result)-1]] {
			if pair.visited == false {
				result = append(result, pair.target)
				pair.visited = true
				if backtracking() {
					return true
				}
				result = result[:len(result)-1]
				pair.visited = false
			}
		}
		return false
	}

	backtracking()

	return result
}

JavaScript

var findItinerary = function(tickets) {
    let result = ['JFK']
    let map = {}

    for (const tickt of tickets) {
        const [from, to] = tickt
        if (!map[from]) {
            map[from] = []
        }
        map[from].push(to)
    }

    for (const city in map) {
        // Sort destination airports
        map[city].sort()
    }
    function backtracing() {
        if (result.length === tickets.length + 1) {
            return true
        }
        if (!map[result[result.length - 1]] || !map[result[result.length - 1]].length) {
            return false
        }
        for(let i = 0 ; i <  map[result[result.length - 1]].length; i++) {
            let city = map[result[result.length - 1]][i]
            // Remove used route, prevent deadlock
            map[result[result.length - 1]].splice(i, 1)
            result.push(city)
            if (backtracing()) {
                return true
            }
            result.pop()
            map[result[result.length - 1]].splice(i, 0, city)
        }
    }
    backtracing()
    return result
};

JavaScript Version 2 Handling Object Key Disorder Issues

/**
 * @param {string[][]} tickets
 * @return {string[]}
 */
var findItinerary = function (tickets) {
	const ans = ["JFK"];
	let map = {};
	// Create a one-to-many relationship between the departure and the destination station, with the destinations sorted
	tickets.forEach((t) => {
		let targets = map[t[0]];
		if (!targets) {
			targets = { [t[1]]: 0 };
			map[t[0]] = targets;
		}
		targets[t[1]] = (targets[t[1]] || 0) + 1;
	});
	// Sort the object by the order of the keys alphabetically
	const sortObject = (obj) => {
		const newObj = {};
		const keys = Object.keys(obj);
		keys.sort((k1, k2) => (k1 < k2 ? -1 : 1));
		keys.forEach((key) => {
			if (obj[key] !== null && typeof obj[key] === "object") {
				newObj[key] = sortObject(obj[key]);
			} else {
				newObj[key] = obj[key];
			}
		});
		return newObj;
	};
	const backtrack = (tickets, targets) => {
		if (ans.length === tickets.length + 1) {
			return true;
		}
		const target = targets[ans[ans.length - 1]];
		// No next stop available
		if (!target) {
			return false;
		}
		// Or sort here
		// const keyList = Object.keys(target).sort((k1, k2) => (k1 < k2 ? -1 : 1));
		const keyList = Object.keys(target);
		for (const key of keyList) {
			// Check if the current station can still fly
			if (target[key] > 0) {
				target[key]--;
				ans.push(key);
				// If the object key is in order, this path is the smallest lexical order, break directly
				if (backtrack(tickets, targets)) {
					return true;
				}
				target[key]++;
				ans.pop();
			}
		}
		return false;
	};
	map = sortObject(map);
	backtrack(tickets, map);
	return ans;
};

TypeScript

function findItinerary(tickets: string[][]): string[] {
    /**
        TicketsMap example:
        { NRT: Map(1) { 'JFK' => 1 }, JFK: Map(2) { 'KUL' => 1, 'NRT' => 1 } }
        Here, the Map data structure is chosen because, unlike Object types, a Map instance maintains the order of key-value pairs.
     */
    type TicketsMap = {
        [index: string]: Map<string, number>
    };
    tickets.sort((a, b) => {
        return a[1] < b[1] ? -1 : 1;
    });
    const ticketMap: TicketsMap = {};
    for (const [from, to] of tickets) {
        if (ticketMap[from] === undefined) {
            ticketMap[from] = new Map();
        }
        ticketMap[from].set(to, (ticketMap[from].get(to) || 0) + 1);
    }
    const resRoute = ['JFK'];
    backTracking(tickets.length, ticketMap, resRoute);
    return resRoute;
    function backTracking(ticketNum: number, ticketMap: TicketsMap, route: string[]): boolean {
        if (route.length === ticketNum + 1) return true;
        const targetMap = ticketMap[route[route.length - 1]];
        if (targetMap !== undefined) {
            for (const [to, count] of targetMap.entries()) {
                if (count > 0) {
                    route.push(to);
                    targetMap.set(to, count - 1);
                    if (backTracking(ticketNum, ticketMap, route) === true) return true;
                    targetMap.set(to, count);
                    route.pop();
                }
            }
        }
        return false;
    }
};

C

typedef struct {
    char *name;        /* key */
    int cnt;           /* Marks whether the destination airport has been flown to */
    UT_hash_handle hh; /* makes this structure hashable */
} to_airport_t;

typedef struct {
    char *name; /* key */
    to_airport_t *to_airports;
    UT_hash_handle hh; /* makes this structure hashable */
} from_airport_t;

void to_airport_destroy(to_airport_t *airports) {
    to_airport_t *airport, *tmp;
    HASH_ITER(hh, airports, airport, tmp) {
        HASH_DEL(airports, airport);
        free(airport);
    }
}

void from_airport_destroy(from_airport_t *airports) {
    from_airport_t *airport, *tmp;
    HASH_ITER(hh, airports, airport, tmp) {
        to_airport_destroy(airport->to_airports);
        HASH_DEL(airports, airport);
        free(airport);
    }
}

int name_sort(to_airport_t *a, to_airport_t *b) {
    return strcmp(a->name, b->name);
}

bool backtracking(from_airport_t *airports, int target_path_len, char **path,
                  int path_len) {
    if (path_len == target_path_len) return true;

    from_airport_t *from_airport = NULL;
    HASH_FIND_STR(airports, path[path_len - 1], from_airport);
    if (!from_airport) return false;

    for (to_airport_t *to_airport = from_airport->to_airports;
         to_airport != NULL; to_airport = to_airport->hh.next) {
        if (to_airport->cnt == 0) continue;
        to_airport->cnt--;
        path[path_len] = to_airport->name;
        if (backtracking(airports, target_path_len, path, path_len + 1))
            return true;
        to_airport->cnt++;
    }
    return false;
}

char **findItinerary(char ***tickets, int ticketsSize, int *ticketsColSize,
                     int *returnSize) {
    from_airport_t *airports = NULL;

    // Record the mapping relationships
    for (int i = 0; i < ticketsSize; i++) {
        from_airport_t *from_airport = NULL;
        to_airport_t *to_airport = NULL;
        HASH_FIND_STR(airports, tickets[i][0], from_airport);
        if (!from_airport) {
            from_airport = malloc(sizeof(from_airport_t));
            from_airport->name = tickets[i][0];
            from_airport->to_airports = NULL;
            HASH_ADD_KEYPTR(hh, airports, from_airport->name,
                            strlen(from_airport->name), from_airport);
        }
        HASH_FIND_STR(from_airport->to_airports, tickets[i][1], to_airport);
        if (!to_airport) {
            to_airport = malloc(sizeof(to_airport_t));
            to_airport->name = tickets[i][1];
            to_airport->cnt = 0;
            HASH_ADD_KEYPTR(hh, from_airport->to_airports, to_airport->name,
                            strlen(to_airport->name), to_airport);
        }
        to_airport->cnt++;
    }

    // Airport sorting
    for (from_airport_t *from_airport = airports; from_airport != NULL;
         from_airport = from_airport->hh.next) {
        HASH_SRT(hh, from_airport->to_airports, name_sort);
    }

    char **path = malloc(sizeof(char *) * (ticketsSize + 1));
    path[0] = "JFK";  // Starting airport
    backtracking(airports, ticketsSize + 1, path, 1);

    from_airport_destroy(airports);

    *returnSize = ticketsSize + 1;
    return path;
}

Swift

Direct iteration through the tickets array:

func findItinerary(_ tickets: [[String]]) -> [String] {
    // First, sort the routes
    let tickets = tickets.sorted { (arr1, arr2) -> Bool in
        if arr1[0] < arr2[0] {
            return true
        } else if arr1[0] > arr2[0] {
            return false
        }
        if arr1[1] < arr2[1] {
            return true
        } else if arr1[1] > arr2[1] {
            return false
        }
        return true
    }
    var path = ["JFK"]
    var used = [Bool](repeating: false, count: tickets.count)

    @discardableResult
    func backtracking() -> Bool {
        // End condition: meeting the total number of routes
        if path.count == tickets.count + 1 { return true }

        for i in 0 ..< tickets.count {
            // Trick! Skip lines that were addressed or whose departure station doesn't align with the last station on path
            guard !used[i], tickets[i][0] == path.last! else { continue }
            // Handle
            used[i] = true
            path.append(tickets[i][1])
            // Recurse
            if backtracking() { return true }
            // Backtrack
            path.removeLast()
            used[i] = false
        }
        return false
    }
    backtracking()
    return path
}

Using a dictionary to optimize iteration and traversal:

func findItinerary(_ tickets: [[String]]) -> [String] {
    // Create a one-to-many relationship between departure stations and destination stations and sort destinations
    typealias Destination = (name: String, used: Bool)
    var targets = [String: [Destination]]()
    for line in tickets {
        let src = line[0], des = line[1]
        var value = targets[src] ?? []
        value.append((des, false))
        targets[src] = value
    }
    for (k, v) in targets {
        targets[k] = v.sorted { $0.name < $1.name }
    }

    var path = ["JFK"]
    let pathCount = tickets.count + 1
    @discardableResult
    func backtracking() -> Bool {
        if path.count == pathCount { return true }

        let startPoint = path.last!
        guard let end = targets[startPoint]?.count, end > 0 else { return false }
        for i in 0 ..< end {
            // Exclude processed routes
            guard !targets[startPoint]![i].used else { continue }
            // Handle
            targets[startPoint]![i].used = true
            path.append(targets[startPoint]![i].name)
            // Recurse
            if backtracking() { return true }
            // Backtrack
            path.removeLast()
            targets[startPoint]![i].used = false
        }
        return false
    }
    backtracking()
    return path
}

Optimizing the creation of the targets dictionary by sorting during insertion:

// Create a one-to-many relationship between departure stations and destination stations, sorting upon creation
typealias Destination = (name: String, used: Bool)
var targets = [String: [Destination]]()
func sortedInsert(_ element: Destination, to array: inout [Destination]) {
    var left = 0, right = array.count - 1
    while left <= right {
        let mid = left + (right - left) / 2
        if array[mid].name < element.name {
            left = mid + 1
        } else if array[mid].name > element.name {
            right = mid - 1
        } else {
            left = mid
            break
        }
    }
    array.insert(element, at: left)
}
for line in tickets {
    let src = line[0], des = line[1]
    var value = targets[src] ?? []
    sortedInsert((des, false), to: &value)
    targets[src] = value
}

Rust

** This approach uses deleting from the hashmap as a workaround due to Rust's ownership issues, which may not allow the previous hashmap approach **

use std::collections::HashMap;
impl Solution {
    fn backtracking(airport: String, targets: &mut HashMap<&String, Vec<&String>>, result: &mut Vec<String>) {
        while let Some(next_airport) = targets.get_mut(&airport).unwrap_or(&mut vec![]).pop() {
            Self::backtracking(next_airport.clone(), targets, result);
        }
        result.push(airport.clone());
    }

    pub fn find_itinerary(tickets: Vec<Vec<String>>) -> Vec<String> {
        let mut targets: HashMap<&String, Vec<&String>> = HashMap::new();
        let mut result = Vec::new();
        for t in 0..tickets.len() {
            targets.entry(&tickets[t][0]).or_default().push(&tickets[t][1]);
        }
        for (_, target) in targets.iter_mut() {
            target.sort_by(|a, b| b.cmp(a));
        }
        Self::backtracking("JFK".to_string(), &mut targets, &mut result);
        result.reverse();
        result
    }
}