17. Letter Combinations of a Phone Number

LeetCode Problem Link (opens new window)

Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent.

The mapping from digits to letters is as follows (same as on telephone keypads). Note that 1 does not map to any letters.

Example:

• Input: "23"
• Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

Note: Although the above answer is in lexicographical order, you can return the answer in any order you want.

Approach

For instance, if the input is "23", the most straightforward idea would be to use two nested for-loops to iterate, which would result in the combinations being output.

If the input is "233", there would be three nested for-loops; if "2333", four nested for-loops...

You should notice a problem similar to 0077.Combinations (opens new window), which is how to write out the number of for-loops layers. At this point, a backtracking algorithm should be considered.

After understanding the problem, you need to solve the following three issues:

1. How to map digits to letters
2. Two letters require two for-loops, three letters require three for-loops, and so on, which is difficult to write in code
3. Handle edge cases like inputting 1, *, # keypad etc.

Mapping Digits to Letters

You can use a map or define a 2D array, for example: string letterMap[10], to do the mapping. Here, I'll define a 2D array, as shown in the following code:

const string letterMap[10] = {
    "",    // 0
    "",    // 1
    "abc", // 2
    "def", // 3
    "ghi", // 4
    "jkl", // 5
    "mno", // 6
    "pqrs",// 7
    "tuv", // 8
    "wxyz" // 9
};

Using Backtracking to Solve the Issue of n Loops

For those who are unfamiliar with the backtracking algorithm, refer to: Backtracking Algorithm Fundamentals (opens new window)

For example, input "23" can be abstracted into a tree structure as shown:

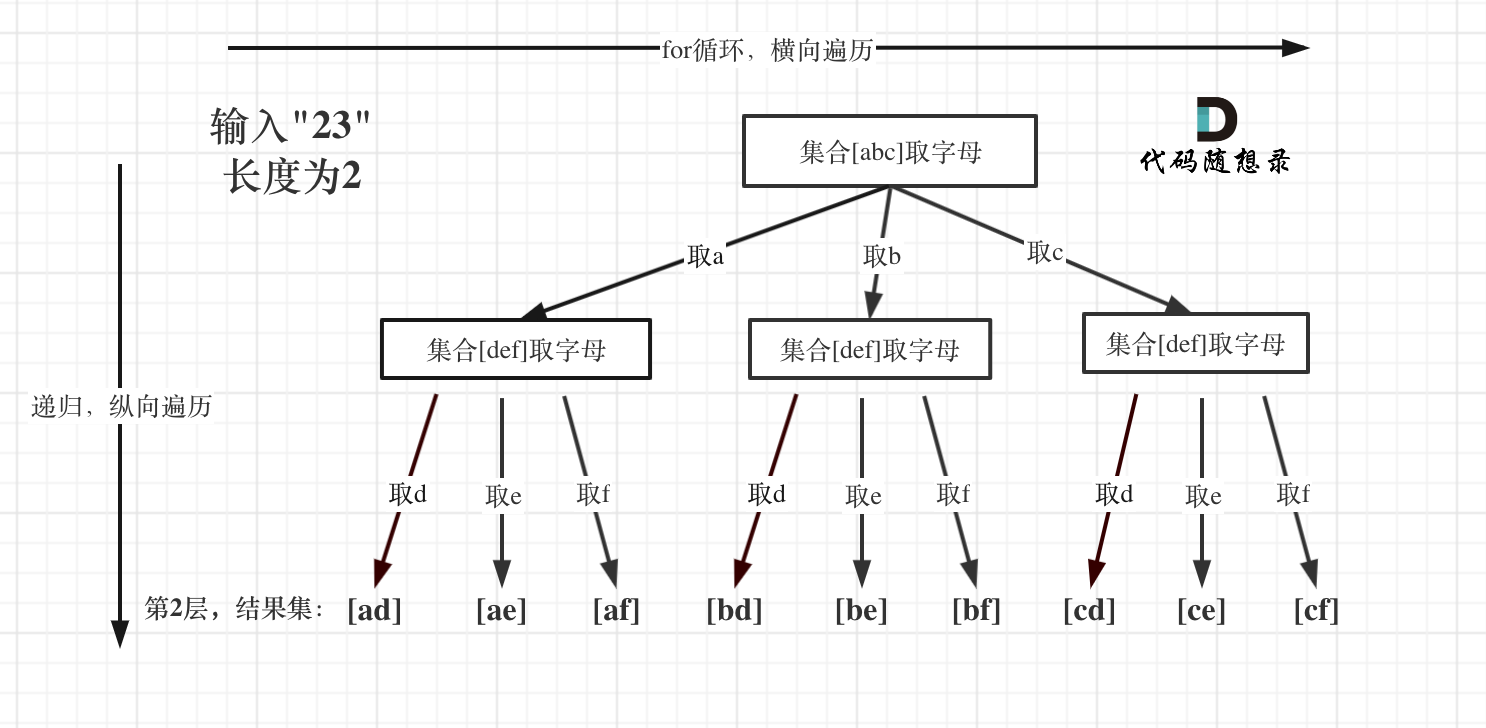
From the diagram, you can see the depth of traversal is the length of the input "23", and the leaf nodes are the results we need to collect, outputting ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

Three steps in backtracking:

• Determine parameters for the backtracking function

First, we need a string s to collect the results of leaf nodes, and then use a string array result to store them, both of which I define as global variables.

Looking at the parameters, they are specified by the problem: string digits and an int type index.

Note that this index is not like the startIndex in 0077.Combinations (opens new window) and 0216.Combination Sum III (opens new window).

This index is used to keep track of which digit is being processed; it is used to traverse digits (the input digit string from the problem) and also represents the depth of the tree.

Here's the code:

vector<string> result;
string s;
void backtracking(const string& digits, int index)

• Determine the termination condition

For example, given the case "23", two digits mean that recursion can go down two levels from the root, and the leaf nodes should be collected as results.

Thus, the termination condition is met when index is equal to the number of digits in digits.size(). Then, collect the result and end the current layer of recursion.

Here's the code:

if (index == digits.size()) {
    result.push_back(s);
    return;
}

• Determine the single-layer traversal logic

Begin by taking the digit that index points to and find the corresponding character set (character set of the phone keypad).

Then a for-loop processes this character set, as follows:

int digit = digits[index] - '0';        // Convert the digit that index points to into an int
string letters = letterMap[digit];      // Get the character set corresponding to the digit
for (int i = 0; i < letters.size(); i++) {
    s.push_back(letters[i]);            // Process
    backtracking(digits, index + 1);    // Recursion, note that index+1 so the next layer processes the next digit
    s.pop_back();                       // Backtracking
}

Note that this for-loop is not starting from startIndex as in Backtracking Algorithm Fundamentals (opens new window) for combinations and combination sums!

This is because we are seeking combinations between different sets in this problem, unlike in 0077.Combinations (opens new window) and 0216.Combination Sum III (opens new window) where combinations are sought within the same set!

Caution: Consider edge cases like inputting 1, *, # keypad, etc.

Although it is good to consider these edge cases in code, the problem's test data should not include such cases, so I did not include them.

However, be aware of these edge cases, especially in live interviews, where they should definitely be considered!

With the key points discussed, it is not difficult to write the following C++ code according to the Backtracking Algorithm Fundamentals (opens new window) template:

// Version 1
class Solution {
private:
    const string letterMap[10] = {
        "", // 0
        "", // 1
        "abc", // 2
        "def", // 3
        "ghi", // 4
        "jkl", // 5
        "mno", // 6
        "pqrs", // 7
        "tuv", // 8
        "wxyz", // 9
    };
public:
    vector<string> result;
    string s;
    void backtracking(const string& digits, int index) {
        if (index == digits.size()) {
            result.push_back(s);
            return;
        }
        int digit = digits[index] - '0';        // Convert the digit that index points to into an int
        string letters = letterMap[digit];      // Get the character set corresponding to the digit
        for (int i = 0; i < letters.size(); i++) {
            s.push_back(letters[i]);            // Process
            backtracking(digits, index + 1);    // Recursion, note that index+1 so the next layer processes the next digit
            s.pop_back();                       // Backtracking
        }
    }
    vector<string> letterCombinations(string digits) {
        s.clear();
        result.clear();
        if (digits.size() == 0) {
            return result;
        }
        backtracking(digits, 0);
        return result;
    }
};

• Time Complexity: O(3^m * 4^n), where m is the number of digits mapping to three letters, and n is the number mapping to four letters.
• Space Complexity: O(3^m * 4^n)

Some code styles involve encapsulating the backtracking process within the recursive function itself, such as in the following code example:

// Version 2
class Solution {
private:
        const string letterMap[10] = {
            "", // 0
            "", // 1
            "abc", // 2
            "def", // 3
            "ghi", // 4
            "jkl", // 5
            "mno", // 6
            "pqrs", // 7
            "tuv", // 8
            "wxyz", // 9
        };
public:
    vector<string> result;
    void getCombinations(const string& digits, int index, const string& s) { // Note the difference in parameters
        if (index == digits.size()) {
            result.push_back(s);
            return;
        }
        int digit = digits[index] - '0';
        string letters = letterMap[digit];
        for (int i = 0; i < letters.size(); i++) {
            getCombinations(digits, index + 1, s + letters[i]);  // Note the difference here
        }
    }
    vector<string> letterCombinations(string digits) {
        result.clear();
        if (digits.size() == 0) {
            return result;
        }
        getCombinations(digits, 0, "");
        return result;
    }
};

I do not recommend hiding backtracking within recursion parameters in this manner because it's not intuitive. I have thoroughly analyzed where backtracking hides in one of my articles, Binary Tree Traversal with Recursion and Backtracking (opens new window).

So, you can write this according to version 1.

Summary

This document outlines the three key points of the problem and emphasizes the differences from previously discussed 0077.Combinations (opens new window) and 0216.Combination Sum III (opens new window). This problem requires finding combinations across multiple sets, requiring attention to certain details during backtracking.

Although this problem is not difficult, it is full of details, and it is important for everyone to practice coding this problem themselves.

Other Language Versions

Java

class Solution {

    // Setup a global list to store the final result
    List<String> list = new ArrayList<>();

    public List<String> letterCombinations(String digits) {
        if (digits == null || digits.length() == 0) {
            return list;
        }
        // Initialize the corresponding numbers, in order to directly map to 2-9, two invalid strings "" are added
        String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        // Iterate and process
        backTracking(digits, numString, 0);
        return list;

    }

    // Every iteration gets a string, so there will be a lot of string concatenation, so here it is more efficient to use StringBuilder
    StringBuilder temp = new StringBuilder();

    // For example, if digits is "23" and num is 0, then str represents the abc corresponding to 2
    public void backTracking(String digits, String[] numString, int num) {
        // Traverse all and record the string obtained once
        if (num == digits.length()) {
            list.add(temp.toString());
            return;
        }
        // str represents the string corresponding to the current num
        String str = numString[digits.charAt(num) - '0'];
        for (int i = 0; i < str.length(); i++) {
            temp.append(str.charAt(i));
            // Recursion, process the next level
            backTracking(digits, numString, num + 1);
            // Remove the last and continue trying
            temp.deleteCharAt(temp.length() - 1);
        }
    }
}

Python

Backtracking

class Solution:
    def __init__(self):
        self.letterMap = [
            "",     # 0
            "",     # 1
            "abc",  # 2
            "def",  # 3
            "ghi",  # 4
            "jkl",  # 5
            "mno",  # 6
            "pqrs", # 7
            "tuv",  # 8
            "wxyz"  # 9
        ]
        self.result = []
        self.s = ""
    
    def backtracking(self, digits, index):
        if index == len(digits):
            self.result.append(self.s)
            return
        digit = int(digits[index])    # Convert the index pointed digit into integer
        letters = self.letterMap[digit]    # Get the character set corresponding to the digit
        for i in range(len(letters)):
            self.s += letters[i]    # Process character
            self.backtracking(digits, index + 1)    # Recursion, note the index +1 for processing the next digit
            self.s = self.s[:-1]    # Backtrack, removing the last added character
    
    def letterCombinations(self, digits):
        if len(digits) == 0:
            return self.result
        self.backtracking(digits, 0)
        return self.result

Concise Backtracking (Version 1)

class Solution:
    def __init__(self):
        self.letterMap = [
            "",     # 0
            "",     # 1
            "abc",  # 2
            "def",  # 3
            "ghi",  # 4
            "jkl",  # 5
            "mno",  # 6
            "pqrs", # 7
            "tuv",  # 8
            "wxyz"  # 9
        ]
        self.result = []
    
    def getCombinations(self, digits, index, s):
        if index == len(digits):
            self.result.append(s)
            return
        digit = int(digits[index])
        letters = self.letterMap[digit]
        for letter in letters:
            self.getCombinations(digits, index + 1, s + letter)
    
    def letterCombinations(self, digits):
        if len(digits) == 0:
            return self.result
        self.getCombinations(digits, 0, "")
        return self.result

Concise Backtracking (Version 2)

class Solution:
    def __init__(self):
        self.letterMap = [
            "",     # 0
            "",     # 1
            "abc",  # 2
            "def",  # 3
            "ghi",  # 4
            "jkl",  # 5
            "mno",  # 6
            "pqrs", # 7
            "tuv",  # 8
            "wxyz"  # 9
        ]
    
    def getCombinations(self, digits, index, s, result):
        if index == len(digits):
            result.append(s)
            return
        digit = int(digits[index])
        letters = self.letterMap[digit]
        for letter in letters:
            self.getCombinations(digits, index + 1, s + letter, result)
    
    def letterCombinations(self, digits):
        result = []
        if len(digits) == 0:
            return result
        self.getCombinations(digits, 0, "", result)
        return result

Backtracking Optimization using List

class Solution:
    def __init__(self):
        self.letterMap = [
            "",     # 0
            "",     # 1
            "abc",  # 2
            "def",  # 3
            "ghi",  # 4
            "jkl",  # 5
            "mno",  # 6
            "pqrs", # 7
            "tuv",  # 8
            "wxyz"  # 9
        ]
    
    def getCombinations(self, digits, index, path, result):
        if index == len(digits):
            result.append(''.join(path))
            return
        digit = int(digits[index])
        letters = self.letterMap[digit]
        for letter in letters:
            path.append(letter)
            self.getCombinations(digits, index + 1, path, result)
            path.pop()
    
    def letterCombinations(self, digits):
        result = []
        if len(digits) == 0:
            return result
        self.getCombinations(digits, 0, [], result)
        return result

Go

The main process is passing the next digit in recursion

var (
    m []string
    path []byte
    res []string
)
func letterCombinations(digits string) []string {
    m = []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
    path, res = make([]byte, 0), make([]string, 0)
    if digits == "" {
        return res
    }
    dfs(digits, 0)
    return res
}
func dfs(digits string, start int) {
    if len(path) == len(digits) {  // Termination condition, string length is equal to the length of digits
        tmp := string(path)
        res = append(res, tmp)
        return
    }
    digit := int(digits[start] - '0')  // Convert the digit pointed by index into an int (confirm the next digit)
    str := m[digit-2]   // Get the character set corresponding to the digit (note the mapping)
    for j := 0; j < len(str); j++ {
        path = append(path, str[j])
        dfs(digits, start+1)
        path = path[:len(path)-1]
    }
}

JavaScript

var letterCombinations = function(digits) {
    const k = digits.length;
    const map = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"];
    if(!k) return [];
    if(k === 1) return map[digits].split("");

    const res = [], path = [];
    backtracking(digits, k, 0);
    return res;

    function backtracking(n, k, a) {
        if(path.length === k) {
            res.push(path.join(""));
            return;
        }
        for(const v of map[n[a]]) {
            path.push(v);
            backtracking(n, k, a + 1);
            path.pop();
        }
    }
};

TypeScript

function letterCombinations(digits: string): string[] {
    if (digits === '') return [];
    const strMap: { [index: string]: string[] } = {
        1: [],
        2: ['a', 'b', 'c'],
        3: ['d', 'e', 'f'],
        4: ['g', 'h', 'i'],
        5: ['j', 'k', 'l'],
        6: ['m', 'n', 'o'],
        7: ['p', 'q', 'r', 's'],
        8: ['t', 'u', 'v'],
        9: ['w', 'x', 'y', 'z'],
    }
    const resArr: string[] = [];
    function backTracking(digits: string, curIndex: number, route: string[]): void {
        if (curIndex === digits.length) {
            resArr.push(route.join(''));
            return;
        }
        let tempArr: string[] = strMap[digits[curIndex]];
        for (let i = 0, length = tempArr.length; i < length; i++) {
            route.push(tempArr[i]);
            backTracking(digits, curIndex + 1, route);
            route.pop();
        }
    }
    backTracking(digits, 0, []);
    return resArr;
};

Rust

const map: [&str; 10] = [
    "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz",
];
impl Solution {
    fn back_trace(result: &mut Vec<String>, s: &mut String, digits: &String, index: usize) {
        let len = digits.len();
        if len == index {
            result.push(s.to_string());
            return;
        }
        let digit = (digits.as_bytes()[index] - b'0') as usize;
        for i in map[digit].chars() {
            s.push(i);
            Self::back_trace(result, s, digits, index + 1);
            s.pop();
        }
    }
    pub fn letter_combinations(digits: String) -> Vec<String> {
        if digits.is_empty() {
            return vec![];
        }
        let mut res = vec![];
        let mut s = String::new();
        Self::back_trace(&mut res, &mut s, &digits, 0);
        res
    }
}

C

char* path;
int pathTop;
char** result;
int resultTop;
char* letterMap[10] = {"", //0
        "", //1
        "abc", //2
        "def", //3
        "ghi", //4
        "jkl", //5
        "mno", //6
        "pqrs", //7
        "tuv", //8
        "wxyz", //9
};
void backTracking(char* digits, int index) {
    // If current index equals length of digits
    if(index == strlen(digits)) {
        // Copy digits array, since it needs to store one more zero, the array length should +1
        char* tempString = (char*)malloc(sizeof(char) * strlen(digits) + 1);
        int j;
        for(j = 0; j < strlen(digits); j++) {
            tempString[j] = path[j];
        }
        // The char array must end with zero
        tempString[strlen(digits)] = 0;
        result[resultTop++] = tempString;
        return;
    }
    // Convert the index pointed digit into int
    int digit = digits[index] - '0';
    // Get the character set corresponding to the digit
    char* letters = letterMap[digit];
    int i;
    for(i = 0; i < strlen(letters); i++) {
        path[pathTop++] = letters[i];
        // Recursion for next level
        backTracking(digits, index+1);
        pathTop--;
    }
}

char ** letterCombinations(char * digits, int* returnSize){
    // Initialize path and result
    path = (char*)malloc(sizeof(char) * strlen(digits));
    result = (char**)malloc(sizeof(char*) * 300);

    *returnSize = 0;
    // If there are zero elements in digits, return empty set
    if(strlen(digits) == 0) 
        return result;
    pathTop = resultTop = 0;
    backTracking(digits, 0);
    *returnSize = resultTop;

    return result;
}

Swift

func letterCombinations(_ digits: String) -> [String] {
    // Mapping between keypad and letter strings
    let letterMap = [
        "",
        "", "abc", "def",
        "ghi", "jkl", "mno",
        "pqrs", "tuv", "wxyz"
    ]
    // Convert input digit string to Int array
    let baseCode = ("0" as Character).asciiValue!
    let digits = digits.map { c in
        guard let code = c.asciiValue else { return -1 }
        return Int(code - baseCode)
    }.filter { $0 >= 0 && $0 <= 9 }
    guard !digits.isEmpty else { return [] }

    var result = [String]()
    var s = ""
    func backtracking(index: Int) {
        // Termination condition: collect results
        if index == digits.count {
            result.append(s)
            return
        }

        // Traverse the current keypad corresponding letter string
        let letters = letterMap[digits[index]]
        for letter in letters {
            s.append(letter) // Process
            backtracking(index: index + 1) // Recursion, remember +1
            s.removeLast() // Backtrack
        }
    }
    backtracking(index: 0)
    return result
}

Scala

object Solution {
  import scala.collection.mutable
  def letterCombinations(digits: String): List[String] = {
    var result = mutable.ListBuffer[String]()
    if(digits == "") return result.toList // If parameter is empty, return empty set in List form
    var path = mutable.ListBuffer[Char]()
    // Mapping of number and character set
    val map = Array[String]("", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz")

    def backtracking(index: Int): Unit = {
      if (index == digits.size) {
        result.append(path.mkString)  // mkString syntax: directly convert array type to string
        return
      }
      var digit = digits(index) - '0' // Must subtract '0' instead of using toInt to avoid errors
      for (i <- 0 until map(digit).size) {
        path.append(map(digit)(i))
        backtracking(index + 1)
        path = path.take(path.size - 1)
      }
    }
    
    backtracking(0)
    result.toList
  }
}

Ruby

def letter_combinations(digits)
  letter_map = {
    2 => ['a','b','c'],
    3 => ['d','e','f'],
    4 => ['g','h','i'],
    5 => ['j','k','l'],
    6 => ['m','n','o'],
    7 => ['p','q','r','s'],
    8 => ['t','u','v'],
    9 => ['w','x','y','z']
  }
  
  result = []
  path = []

  return result if digits.size == 0

  backtracking(result, letter_map, digits.split(''), path, 0)
  result
end

def backtracking(result, letter_map, digits, path, index) 
  if path.size == digits.size
    result << path.join('')
    return
  end

  hash[digits[index].to_i].each do |chr|
    path << chr
    # index + 1 to process the next digit
    backtracking(result, letter_map, digits, path, index + 1)
    # Backtrack, remove last processed digit
    path.pop
  end
end

C#

public class Solution
{
    public IList<string> res = new List<string>();
    public string s;
    public string[] letterMap = new string[10] { "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz" };
    public IList<string> LetterCombinations(string digits)
    {
        if (digits.Length == 0)
            return res;
        BackTracking(digits, 0);
        return res;
    }
    public void BackTracking(string digits, int index)
    {
        if (index == digits.Length)
        {
            res.Add(s);
            return;
        }
        int digit = digits[index] - '0';
        string letters = letterMap[digit];
        for (int i = 0; i < letters.Length; i++)
        {
            s += letters[i];
            BackTracking(digits, index + 1);
            s = s.Substring(0, s.Length - 1);
        }
    }
}