# 93. Restore IP Addresses
LeetCode problem link (opens new window)
Given a string containing only digits, restore it by returning all possible valid IP address combinations. A valid IP address consists of exactly four integers (each integer is between 0 and 255) separated by single dots. For example, "0.1.2.201" and "192.168.1.1" are valid IP addresses, but "0.011.255.245", "192.168.1.312", and "192.168@1.1" are not valid IP addresses.
Example 1:
- Input: s = "25525511135"
- Output: ["255.255.11.135","255.255.111.35"]
Example 2:
- Input: s = "0000"
- Output: ["0.0.0.0"]
Example 3:
- Input: s = "1111"
- Output: ["1.1.1.1"]
Example 4:
- Input: s = "010010"
- Output: ["0.10.0.10","0.100.1.0"]
Example 5:
- Input: s = "101023"
- Output: ["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
Constraints:
- 0 <= s.length <= 3000
- s consists of digits only
# Approach
Before solving this problem, it's beneficial to complete 0131.Palindrome Partitioning (opens new window).
At first glance, this problem might seem puzzling. However, realize that it is a string segmentation problem. Such problems can be tackled using backtracking to explore all possibilities, similar to 0131.Palindrome Partitioning (opens new window).
String segmentation problems can be visualized as tree structures, as illustrated below:
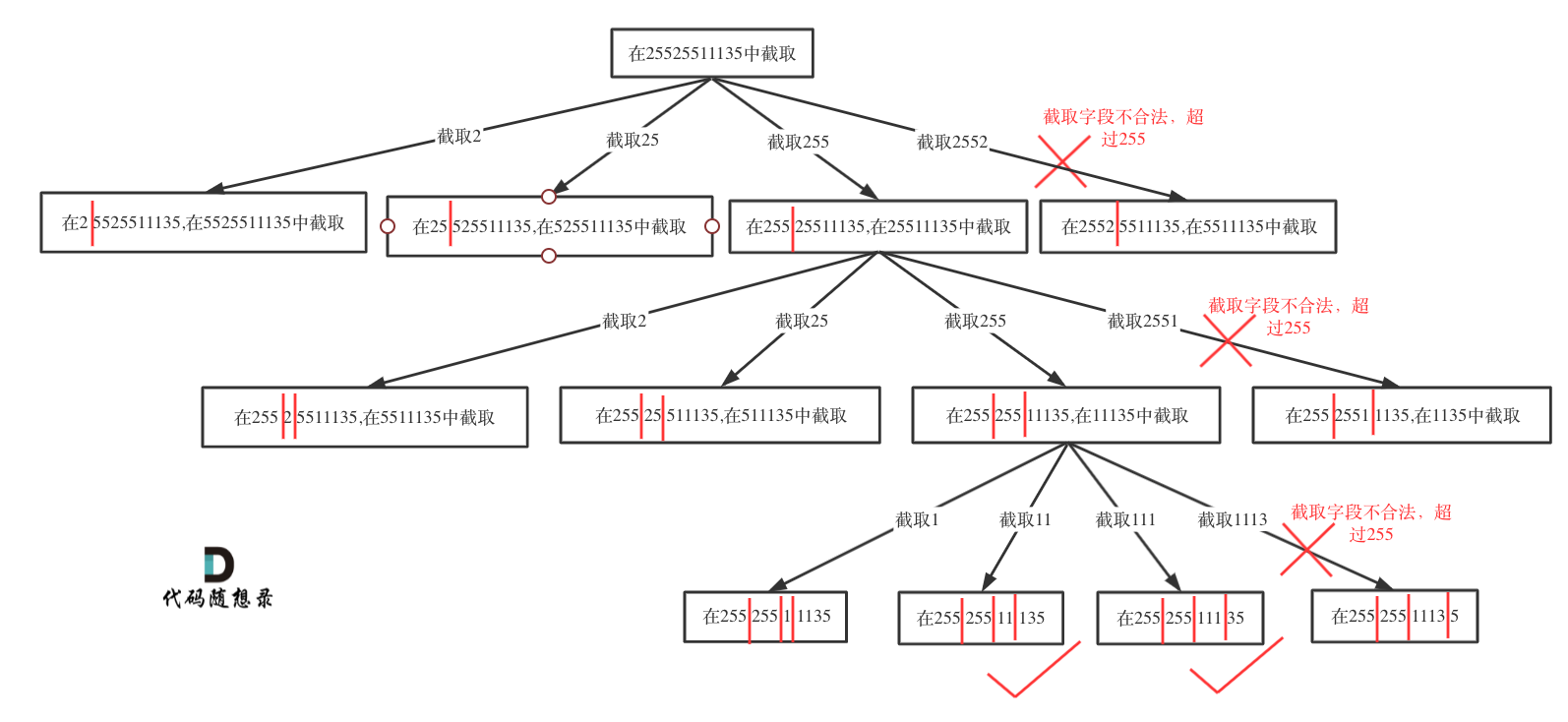
# Backtracking in Three Steps
- Recursive Parameters
In 0131.Palindrome Partitioning (opens new window), we mentioned that segmentation problems are similar to combination problems.
startIndex is needed to prevent overlapping cuts and record the start position for the next level of recursion. We also need a variable pointNum to record the number of dots added.
Thus, the code is as follows:
vector<string> result; // stores results
// startIndex: search start index, pointNum: number of dots added
void backtracking(string& s, int startIndex, int pointNum) {
2
3
- Termination Condition
The termination condition differs from the one in 0131.Palindrome Partitioning (opens new window). Here, we require exactly four segments, so we terminate when the count of segments is four. pointNum indicates the number of dots, and when it's three, it means the string has been divided into four segments.
Afterward, we check if the fourth segment is valid and if so, we add it to the result set.
if (pointNum == 3) { // If the number of dots is 3, segmentation ends
// Check if the fourth substring is valid and add it to the result
if (isValid(s, startIndex, s.size() - 1)) {
result.push_back(s);
}
return;
}
2
3
4
5
6
7
- Single Level Search Logic
In 0131.Palindrome Partitioning (opens new window), we explained how to extract substrings within the loop for (int i = startIndex; i < s.size(); i++). In the range [startIndex, i], you need to check if the substring is valid.
If valid, add the symbol . to indicate segmentation. If not, end the current loop. The pruned branches are shown below:
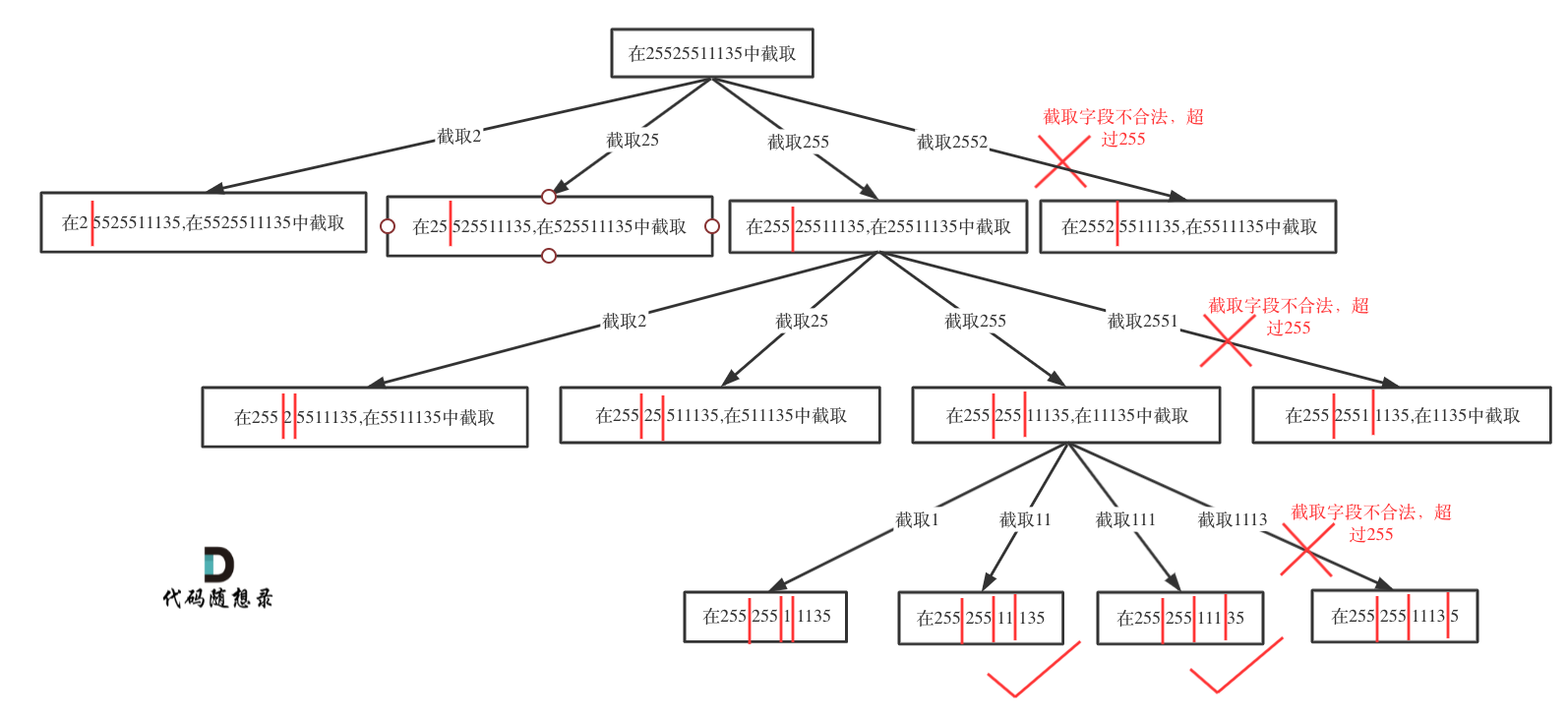
Next is the process of recursion and backtracking:
In the recursive call, the next level's startIndex should be from i+2 (since the symbol . is added to the string), and the count of segments, pointNum, increment by one.
During backtracking, remove the added dot . and decrease pointNum by one.
for (int i = startIndex; i < s.size(); i++) {
if (isValid(s, startIndex, i)) { // Check if the substring in [startIndex, i] is valid
s.insert(s.begin() + i + 1 , '.'); // Insert a dot after the character at index i
pointNum++;
backtracking(s, i + 2, pointNum); // After inserting a dot, the substring's next start is i+2
pointNum--; // Backtrack
s.erase(s.begin() + i + 1); // Backtrack by removing the dot
} else break; // If not valid, end the current loop
}
2
3
4
5
6
7
8
9
# Validation of Substring
Finally, write a method to determine the validity of a segment.
The validation covers the following considerations:
- Segments starting with
0are invalid - Segments with non-numeric characters are invalid
- Segments greater than 255 are invalid
// Validate if the number represented by the substring s in the closed interval [start, end] is valid
bool isValid(const string& s, int start, int end) {
if (start > end) {
return false;
}
if (s[start] == '0' && start != end) { // Numbers starting with 0 are invalid
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] > '9' || s[i] < '0') { // Non-digit characters are invalid
return false;
}
num = num * 10 + (s[i] - '0');
if (num > 255) { // Numbers greater than 255 are invalid
return false;
}
}
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Following the backtracking template from Backtracking Algorithm Fundamentals (opens new window):
void backtracking(parameters) {
if (termination condition) {
store result;
return;
}
for (choice : elements in the current level (the number of children for a node in the tree is the size of the set of choices)) {
process the node;
backtracking(path, choice list); // Recursion
rollback, undo the processing result
}
}
2
3
4
5
6
7
8
9
10
11
12
The C++ code for the backtracking algorithm is as follows:
class Solution {
private:
vector<string> result; // store results
// startIndex: search start index, pointNum: count of dots added
void backtracking(string& s, int startIndex, int pointNum) {
if (pointNum == 3) { // If the number of dots is 3, segmentation ends
// Check if the fourth substring is valid and add it to the result
if (isValid(s, startIndex, s.size() - 1)) {
result.push_back(s);
}
return;
}
for (int i = startIndex; i < s.size(); i++) {
if (isValid(s, startIndex, i)) { // Check if the substring in [startIndex, i] is valid
s.insert(s.begin() + i + 1 , '.'); // Insert a dot after the character at index i
pointNum++;
backtracking(s, i + 2, pointNum); // After inserting a dot, the substring's next start is i+2
pointNum--; // Backtrack
s.erase(s.begin() + i + 1); // Backtrack by removing the dot
} else break; // If not valid, end the current loop
}
}
// Validate if the number represented by the substring s in the closed interval [start, end] is valid
bool isValid(const string& s, int start, int end) {
if (start > end) {
return false;
}
if (s[start] == '0' && start != end) { // Numbers starting with 0 are invalid
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] > '9' || s[i] < '0') { // Non-digit characters are invalid
return false;
}
num = num * 10 + (s[i] - '0');
if (num > 255) { // Numbers greater than 255 are invalid
return false;
}
}
return true;
}
public:
vector<string> restoreIpAddresses(string s) {
result.clear();
if (s.size() < 4 || s.size() > 12) return result; // Consider it as a pruning
backtracking(s, 0, 0);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
- Time Complexity: O(3^4), because the IP address consists of 4 numbers and each number can be split into up to 3 segments, making the maximum depth of the search tree 4, with each node having up to 3 children.
- Space Complexity: O(n)
# Summary
This problem covers the challenges of string segmentation mentioned in 0131.Palindrome Partitioning (opens new window). This problem requires adding commas as separators and validating the intervals, making it a more advanced version of the earlier problem.
The detailed analysis and tree structure diagrams provided should offer clear insights into the problem.
# Other Language Versions
# Java
class Solution {
List<String> result = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
if (s.length() > 12) return result; // Consider it as a pruning
backTrack(s, 0, 0);
return result;
}
// startIndex: search start index, pointNum: count of dots
private void backTrack(String s, int startIndex, int pointNum) {
if (pointNum == 3) {// If the number of dots is 3, segmentation ends
// Check if the fourth segment is valid and add it to result
if (isValid(s,startIndex,s.length()-1)) {
result.add(s);
}
return;
}
for (int i = startIndex; i < s.length(); i++) {
if (isValid(s, startIndex, i)) {
s = s.substring(0, i + 1) + "." + s.substring(i + 1); // Insert a dot after the current segment
pointNum++;
backTrack(s, i + 2, pointNum);// After inserting a dot, the next segment's start is i+2
pointNum--;// Backtrack
s = s.substring(0, i + 1) + s.substring(i + 2);// Backtrack by removing the dot
} else {
break;
}
}
}
// Validate if the number represented by the substring s in the closed interval [start, end] is valid
private Boolean isValid(String s, int start, int end) {
if (start > end) {
return false;
}
if (s.charAt(start) == '0' && start != end) { // Numbers starting with 0 are invalid
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s.charAt(i) > '9' || s.charAt(i) < '0') { // Non-digit characters are invalid
return false;
}
num = num * 10 + (s.charAt(i) - '0');
if (num > 255) { // Numbers greater than 255 are invalid
return false;
}
}
return true;
}
}
// Method 1: Using StringBuilder to optimize time and space complexity since inserting in StringBuilder doesn't require copying the entire string. Avoids substring copying for space optimization.
class Solution {
List<String> result = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
StringBuilder sb = new StringBuilder(s);
backTracking(sb, 0, 0);
return result;
}
private void backTracking(StringBuilder s, int startIndex, int dotCount){
if(dotCount == 3){
if(isValid(s, startIndex, s.length() - 1)){
result.add(s.toString());
}
return;
}
for(int i = startIndex; i < s.length(); i++){
if(isValid(s, startIndex, i)){
s.insert(i + 1, '.');
backTracking(s, i + 2, dotCount + 1);
s.deleteCharAt(i + 1);
}else{
break;
}
}
}
//[start, end]
private boolean isValid(StringBuilder s, int start, int end){
if(start > end)
return false;
if(s.charAt(start) == '0' && start != end)
return false;
int num = 0;
for(int i = start; i <= end; i++){
int digit = s.charAt(i) - '0';
num = num * 10 + digit;
if(num > 255)
return false;
}
return true;
}
}
// Method 2: Better pruning and time complexity optimization compared to the method above
class Solution {
List<String> result = new ArrayList<String>();
StringBuilder stringBuilder = new StringBuilder();
public List<String> restoreIpAddresses(String s) {
restoreIpAddressesHandler(s, 0, 0);
return result;
}
// number represents the number of segments in stringBuilder
public void restoreIpAddressesHandler(String s, int start, int number) {
// If start equals the length of s and the number of segments is 4, add to result and return
if (start == s.length() && number == 4) {
result.add(stringBuilder.toString());
return;
}
// If start equals the length of s but the number of segments is not 4, or if the number of segments is 4 but start is less than the length of s, return directly
if (start == s.length() || number == 4) {
return;
}
// Pruning: the length of a segment is at most 3 and the segment should be in the range [0,255]
for (int i = start; i < s.length() && i - start < 3 && Integer.parseInt(s.substring(start, i + 1)) >= 0
&& Integer.parseInt(s.substring(start, i + 1)) <= 255; i++) {
if (i + 1 - start > 1 && s.charAt(start) - '0' == 0) {
break;
}
stringBuilder.append(s.substring(start, i + 1));
// Only add a dot if the number of segments is less than 3; if it equals 3, it means the last segment doesn't need another dot
if (number < 3) {
stringBuilder.append(".");
}
number++;
restoreIpAddressesHandler(s, i + 1, number);
number--;
// Remove the most recent segment from stringBuilder, considering the potential dot
stringBuilder.delete(start + number, i + number + 2);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
# Python
Backtracking (Version 1)
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
result = []
self.backtracking(s, 0, 0, "", result)
return result
def backtracking(self, s, start_index, point_num, current, result):
if point_num == 3: # If the number of dots is 3, segmentation ends
if self.is_valid(s, start_index, len(s) - 1): # Check if the fourth segment is valid
current += s[start_index:] # Add the last segment
result.append(current)
return
for i in range(start_index, len(s)):
if self.is_valid(s, start_index, i): # Check if the [start_index, i] segment is valid
sub = s[start_index:i + 1]
self.backtracking(s, i + 1, point_num + 1, current + sub + '.', result)
else:
break
def is_valid(self, s, start, end):
if start > end:
return False
if s[start] == '0' and start != end: # Segments starting with 0 are invalid
return False
num = 0
for i in range(start, end + 1):
if not s[i].isdigit(): # Non-digit characters are invalid
return False
num = num * 10 + int(s[i])
if num > 255: # Numbers greater than 255 are invalid
return False
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Backtracking (Version 2)
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
results = []
self.backtracking(s, 0, [], results)
return results
def backtracking(self, s, index, path, results):
if index == len(s) and len(path) == 4:
results.append('.'.join(path))
return
if len(path) > 4: # Pruning
return
for i in range(index, min(index + 3, len(s))):
if self.is_valid(s, index, i):
sub = s[index:i+1]
path.append(sub)
self.backtracking(s, i+1, path, results)
path.pop()
def is_valid(self, s, start, end):
if start > end:
return False
if s[start] == '0' and start != end: # Segments starting with 0 are invalid
return False
num = int(s[start:end+1])
return 0 <= num <= 255
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Backtracking (Version 3)
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
result = []
self.backtracking(s, 0, [], result)
return result
def backtracking(self, s, startIndex, path, result):
if startIndex == len(s):
result.append('.'.join(path[:]))
return
for i in range(startIndex, min(startIndex+3, len(s))):
# If i traversed further but the current address starts with a 0, break
if i > startIndex and s[startIndex] == '0':
break
# For example, if s has length of 5 and currently traversing to i=3
# Without any segments added, remaining elements would be 5-3=2, including i itself
# path contains stored segments, so the count of elements it contains signifies the address count
# (4 - len(path)) * 3 represents the maximum number of elements that can be stored in current path
# 4 - len(path) is the minimum required elements count
if (4 - len(path)) * 3 < len(s) - i or 4 - len(path) > len(s) - i:
break
if i - startIndex == 2:
if not int(s[startIndex:i+1]) <= 255:
break
path.append(s[startIndex:i+1])
self.backtracking(s, i+1, path, result)
path.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Go
var (
path []string
res []string
)
func restoreIpAddresses(s string) []string {
path, res = make([]string, 0, len(s)), make([]string, 0)
dfs(s, 0)
return res
}
func dfs(s string, start int) {
if len(path) == 4 { // Don't continue if there are already four segments
if start == len(s) {
str := strings.Join(path, ".")
res = append(res, str)
}
return
}
for i := start; i < len(s); i++ {
if i != start && s[start] == '0' { // Segments with leading zeros are invalid
break
}
str := s[start : i+1]
num, _ := strconv.Atoi(str)
if num >= 0 && num <= 255 {
path = append(path, str) // Move to the next layer if valid
dfs(s, i+1)
path = path[:len(path) - 1]
} else { // If not valid, move directly to exit
break
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# JavaScript
/**
* @param {string} s
* @return {string[]}
*/
var restoreIpAddresses = function(s) {
const res = [], path = [];
backtracking(0, 0)
return res;
function backtracking(i) {
const len = path.length;
if(len > 4) return;
if(len === 4 && i === s.length) {
res.push(path.join("."));
return;
}
for(let j = i; j < s.length; j++) {
const str = s.slice(i, j + 1);
if(str.length > 3 || +str > 255) break;
if(str.length > 1 && str[0] === "0") break;
path.push(str);
backtracking(j + 1);
path.pop()
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# TypeScript
function isValidIpSegment(str: string): boolean {
let resBool: boolean = true;
let tempVal: number = Number(str);
if (
str.length === 0 || isNaN(tempVal) ||
tempVal > 255 || tempVal < 0 ||
(str.length > 1 && str[0] === '0')
) {
resBool = false;
}
return resBool;
}
function restoreIpAddresses(s: string): string[] {
const resArr: string[] = [];
backTracking(s, 0, []);
return resArr;
function backTracking(s: string, startIndex: number, route: string[]): void {
let length: number = s.length;
if (route.length === 4 && startIndex >= length) {
resArr.push(route.join('.'));
return;
}
if (route.length === 4 || startIndex >= length) return;
let tempStr: string = '';
for (let i = startIndex + 1; i <= Math.min(length, startIndex + 3); i++) {
tempStr = s.slice(startIndex, i);
if (isValidIpSegment(tempStr)) {
route.push(s.slice(startIndex, i));
backTracking(s, i, route);
route.pop();
}
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Rust
impl Solution {
fn is_valid(s: &[char], start: usize, end: usize) -> bool {
if start > end {
return false;
}
if s[start] == '0' && start != end {
return false;
}
let mut num = 0;
for &c in s.iter().take(end + 1).skip(start) {
if !('0'..='9').contains(&c) {
return false;
}
if let Some(digit) = c.to_digit(10) {
num = num * 10 + digit;
}
if num > 255 {
return false;
}
}
true
}
fn backtracking(result: &mut Vec<String>, s: &mut Vec<char>, start_index: usize, mut point_num: usize) {
let len = s.len();
if point_num == 3 {
if Self::is_valid(s, start_index, len - 1) {
result.push(s.iter().collect::<String>());
}
return;
}
for i in start_index..len {
if Self::is_valid(s, start_index, i) {
point_num += 1;
s.insert(i + 1, '.');
Self::backtracking(result, s, i + 2, point_num);
point_num -= 1;
s.remove(i + 1);
} else { break; }
}
}
pub fn restore_ip_addresses(s: String) -> Vec<String> {
let mut result: Vec<String> = Vec::new();
let len = s.len();
if len < 4 || len > 12 { return result; }
let mut s = s.chars().collect::<Vec<char>>();
Self::backtracking(&mut result, &mut s, 0, 0);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# C
// Stores the result
char** result;
int resultTop;
// Records the positions where dots are added
int segments[3];
int isValid(char* s, int start, int end) {
if(start > end)
return 0;
if (s[start] == '0' && start != end) { // Numbers with leading 0s are invalid
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] > '9' || s[i] < '0') { // Non-digit characters are invalid
return false;
}
num = num * 10 + (s[i] - '0');
if (num > 255) { // Numbers greater than 255 are invalid
return false;
}
}
return true;
}
// startIndex is the index to begin search, pointNum is the count of dots
void backTracking(char* s, int startIndex, int pointNum) {
// If the number of dots is 3, segmentation ends
if(pointNum == 3) {
// If the last segment is valid, add the current string to result
if(isValid(s, startIndex, strlen(s) - 1)) {
char* tempString = (char*)malloc(sizeof(char) * strlen(s) + 4);
int j;
// Records the index for adding characters to tempString
int count = 0;
// Records the count of dots used during insertion
int count1 = 0;
for(j = 0; j < strlen(s); j++) {
tempString[count++] = s[j];
// If dots used less than 3 and the current index equals dot index, add a dot to the array
if(count1 < 3 && j == segments[count1]) {
tempString[count++] = '.';
count1++;
}
}
tempString[count] = 0;
// Expand result array
result = (char**)realloc(result, sizeof(char*) * (resultTop + 1));
result[resultTop++] = tempString;
}
return ;
}
int i;
for(i = startIndex; i < strlen(s); i++) {
if(isValid(s, startIndex, i)) {
// Record positions to add dots
segments[pointNum] = i;
backTracking(s, i + 1, pointNum + 1);
}
else {
break;
}
}
}
char ** restoreIpAddresses(char * s, int* returnSize){
result = (char**)malloc(0);
resultTop = 0;
backTracking(s, 0, 0);
*returnSize = resultTop;
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
# Swift
// Validate if an IP segment is legitimate
func isValid(s: [Character], start: Int, end: Int) -> Bool {
guard start <= end, start >= 0, end < s.count else { return false } // Invalid index
if start != end, s[start] == "0" { return false } // Multi-digit numbers starting with 0 are invalid
var num = 0
for i in start ... end {
let c = s[i]
guard c >= "0", c <= "9" else { return false } // Non-numeric characters are invalid
let value = c.asciiValue! - ("0" as Character).asciiValue!
num = num * 10 + Int(value)
guard num <= 255 else { return false } // Numbers greater than 255 are invalid
}
return true
}
func restoreIpAddresses(_ s: String) -> [String] {
var s = Array(s) // Convert to character array for easier comparison
var result = [String]() // Result
func backtracking(startIndex: Int, pointCount: Int) {
guard startIndex < s.count else { return } // Invalid index
// Ending condition
if pointCount == 3 {
// If the last segment is valid, collect the result
if isValid(s: s, start: startIndex, end: s.count - 1) {
result.append(String(s))
}
return
}
for i in startIndex ..< s.count {
// Validate [starIndex, i] substring, if valid, insert ".", if not terminate this iteration
if isValid(s: s, start: startIndex, end: i) {
s.insert(".", at: i + 1) // Insert "." after the substring
backtracking(startIndex: i + 2, pointCount: pointCount + 1) // Note the jump by 2 here, and pointCount + 1 hides the pointCount's backtracking
s.remove(at: i + 1) // Backtrack
} else {
break
}
}
}
backtracking(startIndex: 0, pointCount: 0)
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# Scala
object Solution {
import scala.collection.mutable
def restoreIpAddresses(s: String): List[String] = {
var result = mutable.ListBuffer[String]()
if (s.size < 4 || s.length > 12) return result.toList
var path = mutable.ListBuffer[String]()
// Validate if a segment of IP is correct
def isIP(sub: String): Boolean = {
if (sub.size > 1 && sub(0) == '0') return false
if (sub.toInt > 255) return false
true
}
def backtracking(startIndex: Int): Unit = {
if (startIndex >= s.size) {
if (path.size == 4) {
result.append(path.mkString(".")) // mkString method connects elements in the collection with the specified string
return
}
return
}
// subString
for (i <- startIndex until startIndex + 3 if i < s.size) {
var subString = s.substring(startIndex, i + 1)
if (isIP(subString)) { // If valid, proceed to the next round
path.append(subString)
backtracking(i + 1)
path = path.take(path.size - 1)
}
}
}
backtracking(0)
result.toList
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# C#
public class Solution
{
public IList<string> res = new List<string>();
public IList<string> RestoreIpAddresses(string s)
{
if (s.Length < 4 || s.Length > 12) return res;
BackTracking(s, 0, 0);
return res;
}
public void BackTracking(string s, int start, int pointSum)
{
if (pointSum == 3)
{
if (IsValid(s, start, s.Length - 1))
{
res.Add(s);
}
return;
}
for (int i = start; i < s.Length; i++)
{
if (IsValid(s, start, i))
{
s = s.Insert(i + 1, ".");
BackTracking(s, i + 2, pointSum + 1);
s = s.Remove(i + 1, 1);
}
else break;
}
}
public bool IsValid(string s, int start, int end)
{
if (start > end) return false;
if (s[start] == '0' && start != end) return false;
int num = 0;
for (int i = start; i <= end; i++)
{
if (s[i] > '9' || s[i] < '0') return false;
num = num * 10 + s[i] - '0';
if (num > 255) return false;
}
return true;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
