Don't be fooled by the fact that this is Combination Sum III instead of Combination Sum; this problem is just right in difficulty compared to the previous 77. Combinations!

216. Combination Sum III

LeetCode Problem Link (opens new window)

Find all valid combinations of k numbers that sum up to n such that the only numbers used are from 1 to 9, and each number is used at most once.

Note:

• All numbers are positive integers.
• The solution set must not contain duplicate combinations.

Example 1: Input: k = 3, n = 7 Output: [[1,2,4]]

Example 2: Input: k = 3, n = 9 Output: [[1,2,6], [1,3,5], [2,3,4]]

Thought Process

The problem is essentially finding combinations of k numbers that sum to n from a fixed set of numbers [1,2,3,4,5,6,7,8,9].

Compared to 77. Combinations (opens new window), this problem introduces an additional constraint: it requires the combination of k numbers that sum to n, with the set of numbers already being fixed to [1,...,9].

Understanding this, after solving 77. Combinations (opens new window), this problem becomes relatively simpler.

In this task, k corresponds to the depth of the tree, while the 9 numbers form the width of the tree.

For example, if k = 2 and n = 4, we need to find combinations of k numbers from the set [1,2,3,4,5,6,7,8,9] where the sum equals n.

The selection process is illustrated as follows:

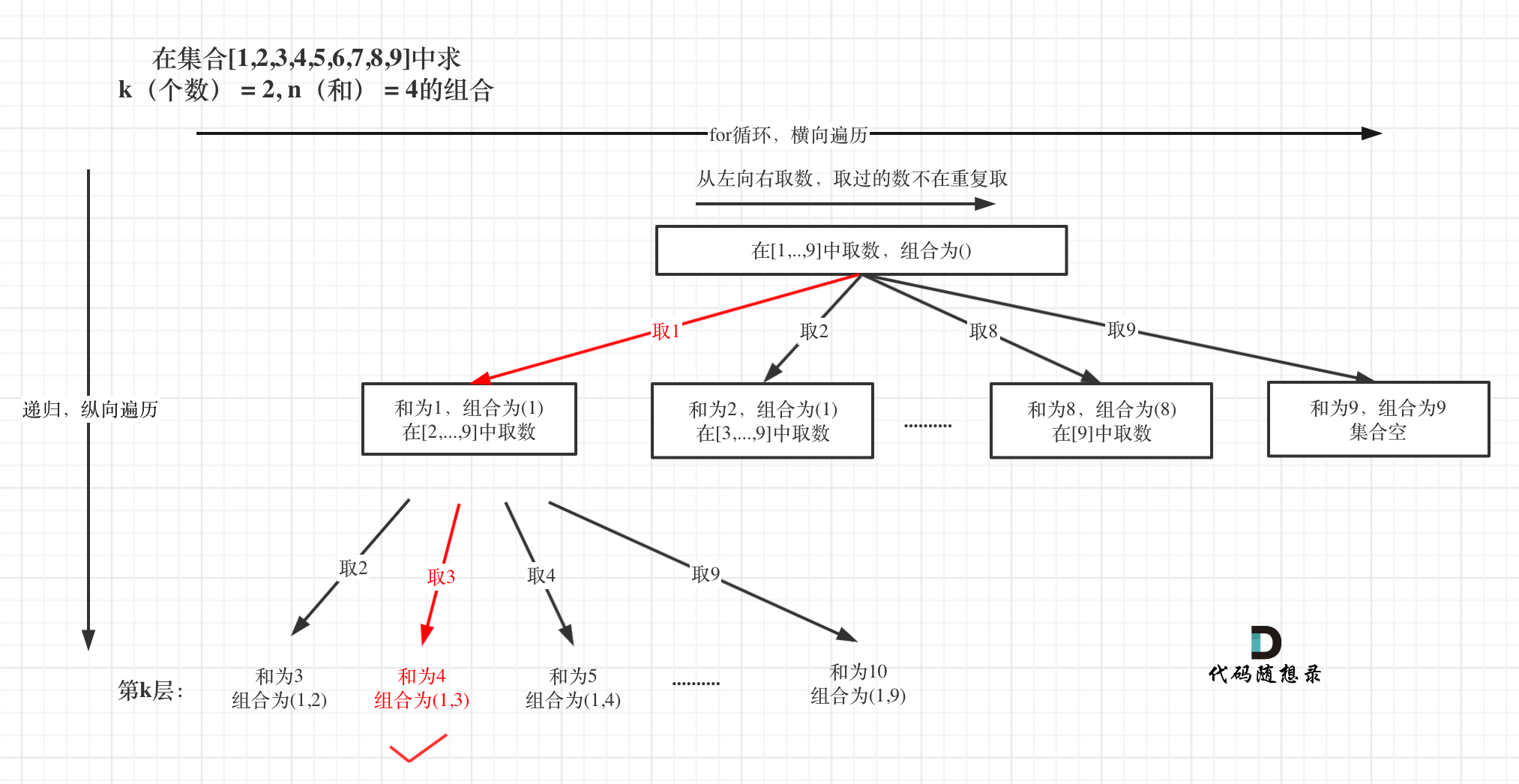
In the example, only the combination (1, 3) sums to 4, meeting the condition.

Backtracking in Three Steps

• Determine the parameters for the recursive function

Similar to 77. Combinations (opens new window), we need a one-dimensional array path to store valid results and a two-dimensional array result to store the result set.

Here, I also define path and result as global variables.

As for why it is named path—it represents a path from the root node to a leaf node in the tree structure.

vector<vector<int>> result; // Stores the result set
vector<int> path; // Stores valid combinations

Next, we need the following parameters:

• targetSum (int) is the target sum, essentially the parameter n.
• k (int) is the number of numbers required, corresponding to the input k.
• sum (int) is the sum of the collected elements in the path, i.e., the sum of elements in path.
• startIndex (int) is the starting position for the next level of the for loop search.

The code is as follows:

vector<vector<int>> result;
vector<int> path;
void backtracking(int targetSum, int k, int sum, int startIndex)

The parameter sum can be omitted, and you can simply deduct the selected element's value from targetSum, checking if targetSum becomes zero. However, for clarity, I've chosen to include the sum parameter.

It should be emphasized again that determining the parameters for the recursive function in backtracking is challenging to get right on the first try. Generally, you will add parameters as needed while writing out the logic.

• Determine the termination condition

When should it terminate?

As mentioned earlier, k limits the depth of the tree since only k elements are selected—further depth is unnecessary.

Thus, if path.size() equals k, it stops.

If the sum of the elements in path (sum) equals targetSum, we collect the current result with result.

The termination condition is thus:

if (path.size() == k) {
    if (sum == targetSum) result.push_back(path);
    return; // Directly return if path.size() == k but sum != targetSum
}

• Single-level search process

The key difference between this and 77. Combinations (opens new window) is the fixed set of numbers, [1,...,9], so the for loop is fixed to i <= 9.

For instance, if k = 3, n = 9:

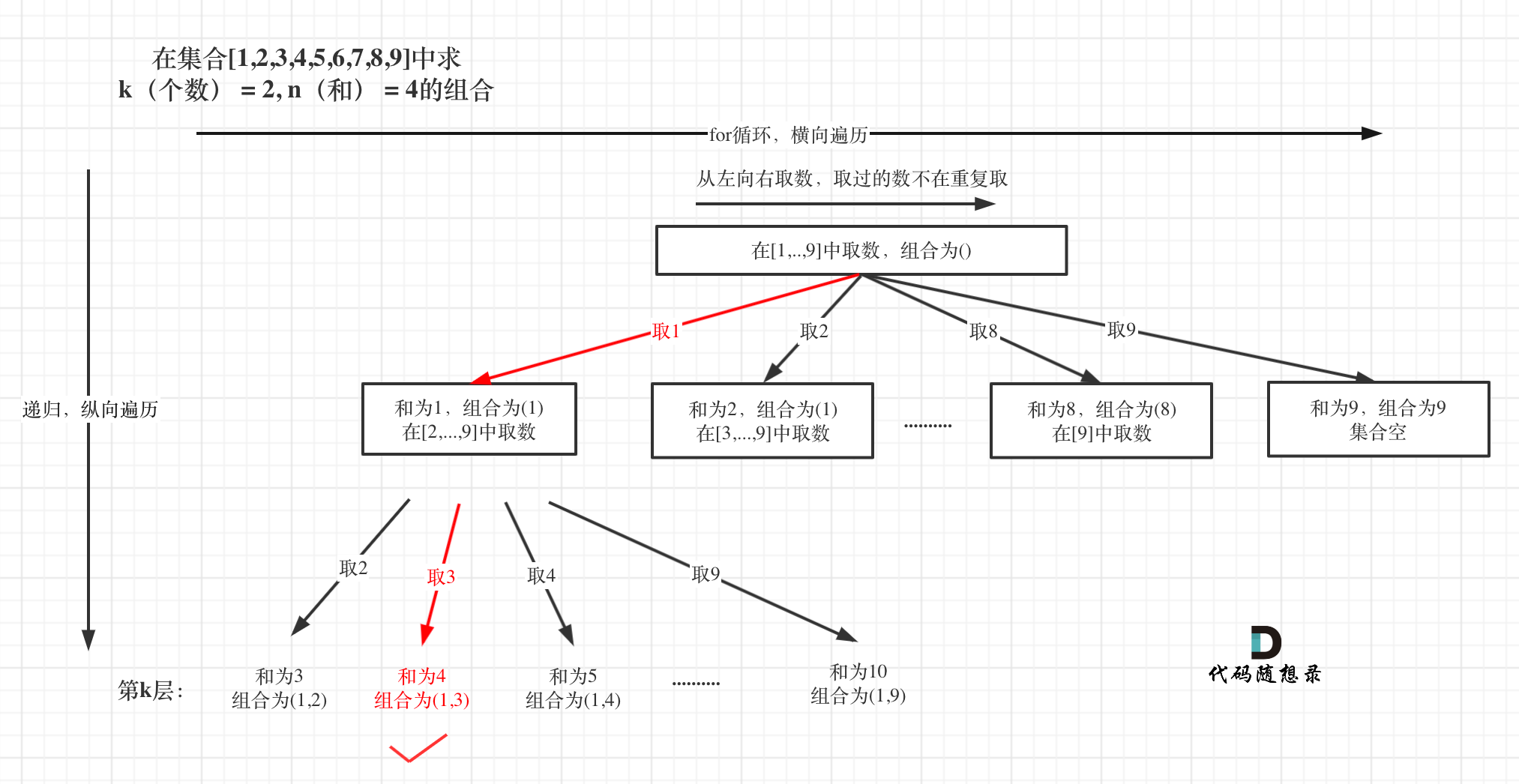
During processing, path collects each selected element, acting like edges in the tree structure, and sum keeps track of the total sum of elements in path.

The code:

for (int i = startIndex; i <= 9; i++) {
    sum += i;
    path.push_back(i);
    backtracking(targetSum, k, sum, i + 1); // Note the adjustment to startIndex using i + 1
    sum -= i; // Backtrack
    path.pop_back(); // Backtrack
}

Ensure there is one-to-one correspondence between processing and backtracking—if you add during processing, subtract during backtracking!

Following the template provided in Backtracking Algorithm Fundamentals (opens new window), writing out the C++ code is straightforward:

class Solution {
private:
    vector<vector<int>> result; // Stores result set
    vector<int> path; // Stores valid combinations
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; 
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i;
            path.push_back(i);
            backtracking(targetSum, k, sum, i + 1); // Adjust startIndex with i + 1
            sum -= i; // Backtrack
            path.pop_back(); // Backtrack
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); 
        path.clear();   
        backtracking(n, k, 0, 1);
        return result;
    }
};

Pruning

For this problem, pruning is a natural strategy and may have already occurred to you while examining the tree structure above.

As depicted:

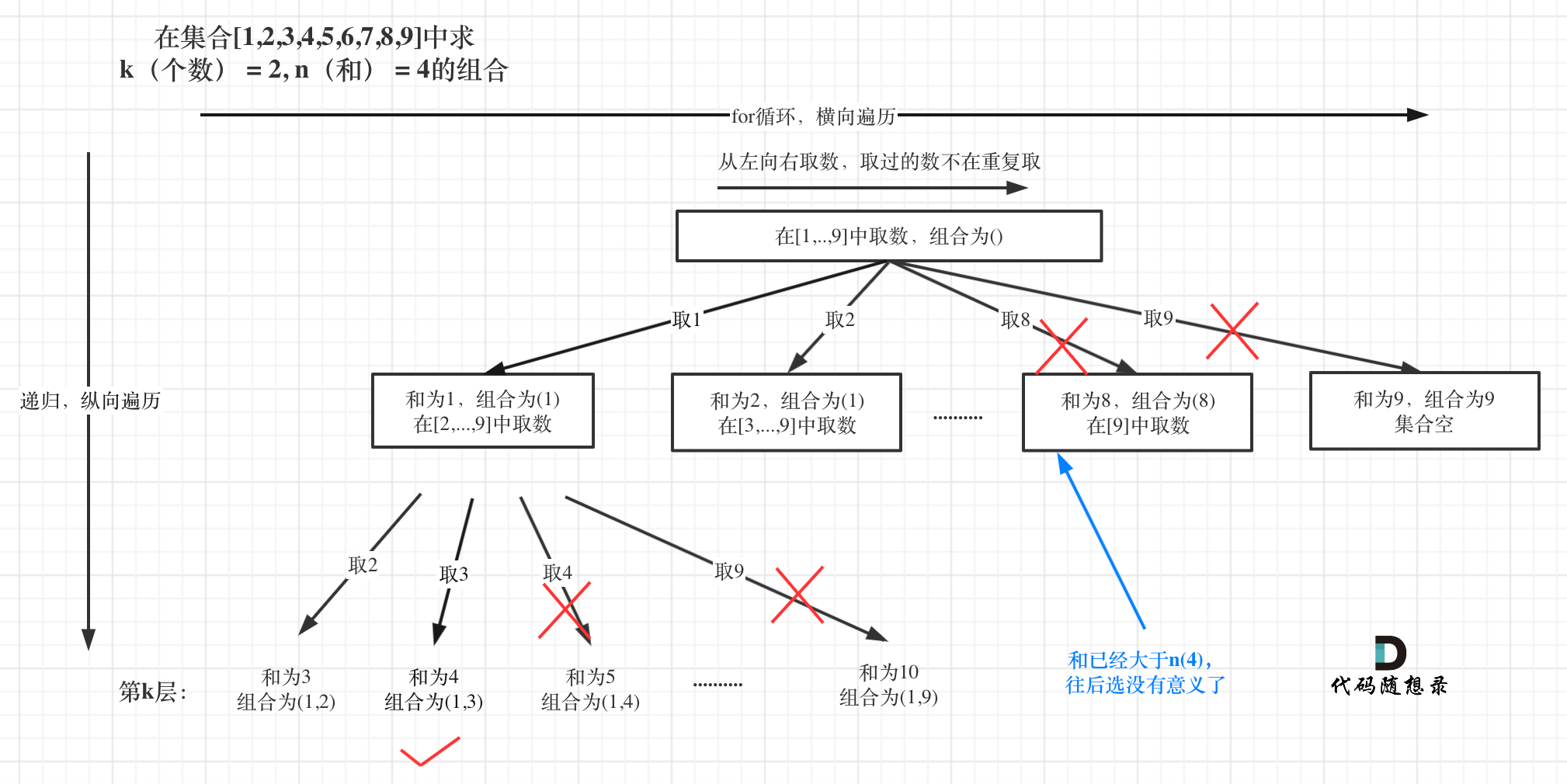
If the sum of selected elements already exceeds n (shown as 4), further exploration is meaningless, and it is pruned directly.

Pruning can be specified at the beginning of the recursive function with the following code:

if (sum > targetSum) { // Pruning operation
    return;
}

Alternatively, this pruning can be placed before invoking the recursive call, but remember to perform backtracking prior to pruning:

for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) { 
    sum += i;
    path.push_back(i);
    if (sum > targetSum) { 
        sum -= i;
        path.pop_back();
        return;
    }
    backtracking(targetSum, k, sum, i + 1); 
    sum -= i; 
    path.pop_back();
}

Similar to 0077. Combination Optimization (opens new window), the range of the for loop can also be pruned to i <= 9 - (k - path.size()) + 1.

The final C++ code is as follows:

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (sum > targetSum) {
            return; 
        }
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; 
        }
        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
            sum += i;
            path.push_back(i);
            backtracking(targetSum, k, sum, i + 1); 
            sum -= i;
            path.pop_back();
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear();
        path.clear();
        backtracking(n, k, 0, 1);
        return result;
    }
};

• Time Complexity: O(n * 2^n)
• Space Complexity: O(n)

Summary

The beginning introduced the differences between this problem and 77. Combinations (opens new window), focusing on the added constraint of summing elements. Solving this is a suitable next step after tackling 77. Combinations (opens new window).

By abstracting the problem into a tree structure and following a three-step backtracking approach, complete with a provision for pruning, clarity is achieved.

Upon completion, you should have a basic understanding of combination problems across different scenarios.

Additional Language Versions

Java

Template Method

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();

    public List<List<Integer>> combinationSum3(int k, int n) {
        backTracking(n, k, 1, 0);
        return result;
    }

    private void backTracking(int targetSum, int k, int startIndex, int sum) {
        if (sum > targetSum) {
            return;
        }

        if (path.size() == k) {
            if (sum == targetSum) result.add(new ArrayList<>(path));
            return;
        }

        for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++) {
            path.add(i);
            sum += i;
            backTracking(targetSum, k, i + 1, sum);
            path.removeLast();
            sum -= i;
        }
    }
}

// Alternatively with condition `if (path.size() > k) return;` for comprehension
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> ans = new ArrayList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        build(k, n, 1, 0);
        return ans;
    }

    private void build(int k, int n, int startIndex, int sum) {

        if (sum > n) return;

        if (path.size() > k) return;

        if (sum == n && path.size() == k) {
            ans.add(new ArrayList<>(path));
            return;
        }

        for(int i = startIndex; i <= 9; i++) {
            path.add(i);
            sum += i;
            build(k, n, i + 1, sum);
            sum -= i;
            path.removeLast();
        }
    }
}

Python

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        result = [] 
        self.backtracking(n, k, 0, 1, [], result)
        return result

    def backtracking(self, targetSum, k, currentSum, startIndex, path, result):
        if currentSum > targetSum:
            return 
        if len(path) == k:
            if currentSum == targetSum:
                result.append(path[:])
            return
        for i in range(startIndex, 9 - (k - len(path)) + 2):
            currentSum += i
            path.append(i)
            self.backtracking(targetSum, k, currentSum, i + 1, path, result)
            currentSum -= i
            path.pop()

Go

var (
    res [][]int
    path  []int
)
func combinationSum3(k int, n int) [][]int {
    res, path = make([][]int, 0), make([]int, 0, k)
    dfs(k, n, 1, 0)
    return res
}

func dfs(k, n int, start int, sum int) {
    if len(path) == k {
        if sum == n {
            tmp := make([]int, k)
            copy(tmp, path)
            res = append(res, tmp)
        }
        return
    }
    for i := start; i <= 9; i++ {
        if sum + i > n || 9-i+1 < k-len(path) {
            break
        }
        path = append(path, i)
        dfs(k, n, i+1, sum+i)
        path = path[:len(path)-1]
    }
}

JavaScript

• Without pruning:

/**
 * @param {number} k
 * @param {number} n
 * @return {number[][]}
 */
var combinationSum3 = function (k, n) {
  var result = [],
    path = [];
  const backtracking = (_k, targetSum, sum, startIndex) => {
    if (path.length === _k) {
      if (sum === targetSum) {
        result.push(path.slice());
      }
      return;
    }

    for (let i = startIndex; i <= 9; i++) {
      path.push(i);
      sum += i;
      backtracking(_k, targetSum, sum, i + 1);
      sum -= i;
      path.pop();
    }
  };
  backtracking(k, n, 0, 1);
  return result;
};

• With pruning:

/**
 * @param {number} k
 * @param {number} n
 * @return {number[][]}
 */
var combinationSum3 = function (k, n) {
  var result = [],
    path = [];
  const backtracking = (_k, targetSum, sum, startIndex) => {
    if (sum > targetSum) {
      return;
    }
    if (path.length === _k) {
      if (sum === targetSum) {
        result.push(path.slice());
      }
      return;
    }

    for (let i = startIndex; i <= 9 - (_k - path.length) + 1; i++) {
      path.push(i);
      sum += i;
      backtracking(_k, targetSum, sum, i + 1);
      sum -= i;
      path.pop();
    }
  };
  backtracking(k, n, 0, 1);
  return result;
};

TypeScript

function combinationSum3(k: number, n: number): number[][] {
    const resArr: number[][] = [];
    function backTracking(k: number, n: number, sum: number, startIndex: number, tempArr: number[]): void {
        if (sum > n) return;
        if (tempArr.length === k) {
            if (sum === n) {
                resArr.push(tempArr.slice());
            }
            return;
        }
        for (let i = startIndex; i <= 9 - (k - tempArr.length) + 1; i++) {
            tempArr.push(i);
            backTracking(k, n, sum + i, i + 1, tempArr);
            tempArr.pop();
        }
    }
    backTracking(k, n, 0, 1, []);
    return resArr;
};

Rust

impl Solution {
    pub fn combination_sum3(k: i32, n: i32) -> Vec<Vec<i32>> {
        let mut result = vec![];
        let mut path = vec![];
        Self::backtrace(&mut result, &mut path, n, k, 0, 1);
        result
    }
    pub fn backtrace(
        result: &mut Vec<Vec<i32>>,
        path: &mut Vec<i32>,
        target_sum: i32,
        k: i32,
        sum: i32,
        start_index: i32,
    ) {
        if sum > target_sum {
            return;
        }
        let len = path.len() as i32;
        if len == k {
            if sum == target_sum {
                result.push(path.to_vec());
            }
            return;
        }
        for i in start_index..=9 - (k - len) + 1 {
            path.push(i);
            Self::backtrace(result, path, target_sum, k, sum + i, i + 1);
            path.pop();
        }
    }
}

C

int* path;
int pathTop;
int** ans;
int ansTop;
int getPathSum() {
    int i;
    int sum = 0;
    for(i = 0; i < pathTop; i++) {
        sum += path[i];
    }
    return sum;
}

void backtracking(int targetSum, int k, int sum, int startIndex) {
    if(pathTop == k) {
        if(sum == targetSum) {
            int* tempPath = (int*)malloc(sizeof(int) * k);
            int j;
            for(j = 0; j < k; j++)
                tempPath[j] = path[j];
            ans[ansTop++] = tempPath;
        }
        return;
    }
    int i;
    for (i = startIndex; i <= 9; i++) {
        sum += i;
        path[pathTop++] = i;
        backtracking(targetSum, k, sum, i + 1);
        sum -= i;
        pathTop--;
    }
}

int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes){
    path = (int*)malloc(sizeof(int) * k);
    ans = (int**)malloc(sizeof(int*) * 20);
    pathTop = ansTop = 0;

    backtracking(n, k, 0, 1);

    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = k;
    }
    return ans;
}

Swift

func combinationSum3(_ count: Int, _ targetSum: Int) -> [[Int]] {
    var result = [[Int]]()
    var path = [Int]()
    func backtracking(sum: Int, start: Int) {
        if sum > targetSum { return }
        if path.count == count {
            if sum == targetSum {
                result.append(path)
            }
            return
        }

        let end = 9
        guard start <= end else { return }
        for i in start ... end {
            path.append(i)
            backtracking(sum: sum + i, start: i + 1)
            path.removeLast()
        }
    }

    backtracking(sum: 0, start: 1)
    return result
}

Scala

object Solution {
  import scala.collection.mutable
  def combinationSum3(k: Int, n: Int): List[List[Int]] = {
    var result = mutable.ListBuffer[List[Int]]()
    var path = mutable.ListBuffer[Int]()

    def backtracking(k: Int, n: Int, sum: Int, startIndex: Int): Unit = {
      if (sum > n) return
      if (sum == n && path.size == k) {
        result.append(path.toList)
        return
      }

      for (i <- startIndex to (9 - (k - path.size) + 1)) {
        path.append(i)
        backtracking(k, n, sum + i, i + 1)
        path = path.take(path.size - 1)
      }
    }

    backtracking(k, n, 0, 1)
    result.toList
  }
}

C#

public class Solution
{
    public IList<IList<int>> res = new List<IList<int>>();
    public IList<int> path = new List<int>();
    public IList<IList<int>> CombinationSum3(int k, int n)
    {
        BackTracking(k, n, 0, 1);
        return res;
    }
    public void BackTracking(int k, int n, int sum, int start)
    {
        if (path.Count == k)
        {
            if (sum == n)
                res.Add(new List<int>(path));
            return;
        }
        for (int i = start; i <= 9; i++)
        {
            sum += i;
            path.Add(i);
            BackTracking(k, n, sum, i + 1);
            sum -= i;
            path.RemoveAt(path.Count - 1);
        }
    }
}
// With pruning
public class Solution
{
    public IList<IList<int>> res = new List<IList<int>>();
    public IList<int> path = new List<int>();
    public IList<IList<int>> CombinationSum3(int k, int n)
    {
        BackTracking(k, n, 0, 1);
        return res;
    }
    public void BackTracking(int k, int n, int sum, int start)
    {
        if (sum > n)
            return;
        if (path.Count == k)
        {
            if (sum == n)
                res.Add(new List<int>(path));
            return;
        }
        for (int i = start; i <= 9 - (k - path.Count) + 1; i++)
        {
            sum += i;
            path.Add(i);
            BackTracking(k, n, sum, i + 1);
            sum -= i;
            path.RemoveAt(path.Count - 1);
        }
    }
}