# 46. Permutations
LeetCode Problem Link (opens new window)
Given a sequence of numbers without duplicates, return all its possible permutations.
Example:
- Input: [1,2,3]
- Output: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
# Idea
Now that we have learned 0077.Combinations (opens new window), 131.Palindrome Partitioning (opens new window), and 78.Subsets (opens new window), let's take a look at the permutation problem.
I believe that even if you were to use a brute force approach to search through all results manually, this brute force method wouldn't be easy to write.
As discussed in Backtracking Algorithm Fundamentals (opens new window), why do we use backtracking despite its inefficiency?
Because being able to arrive at the solution through brute force itself is quite remarkable!
Let's take [1,2,3] as an example and visualize it as a tree structure below:
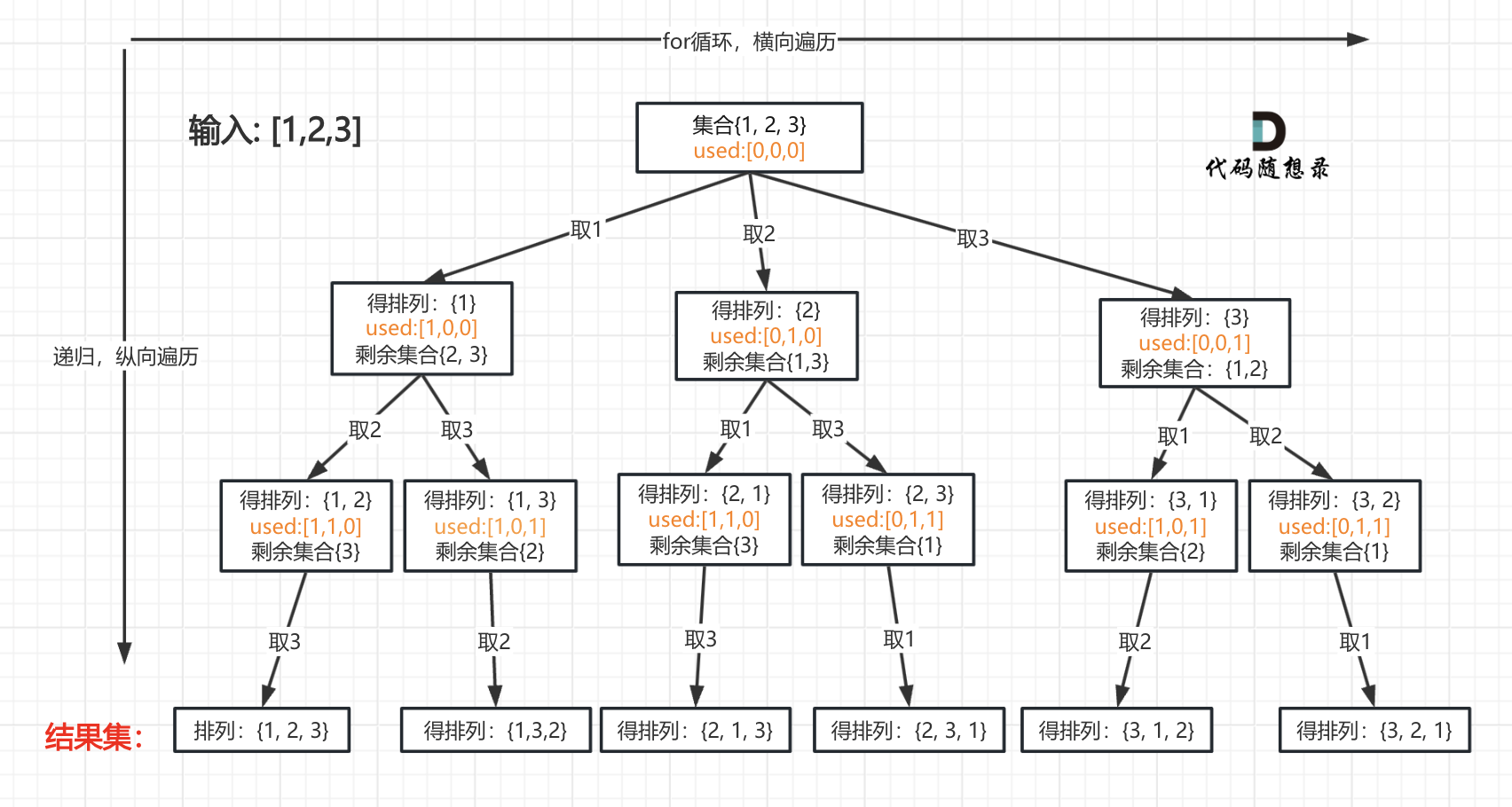
# Three Steps of Backtracking
- Recursive Function Parameters
First, permutations are ordered, meaning [1,2] and [2,1] are different sets, which is different from the subset and combination problems we analyzed before.
We can see that element 1 has been used in [1,2], but it needs to be used again in [2,1], so when dealing with permutation problems, there's no need for the startIndex.
However, permutation problems require a used array to mark the elements that have already been selected, as indicated by the orange part in the illustration:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used)
2
3
- Termination Condition of Recursion

As we can see, leaf nodes are where we gather results.
When do we know we have reached a leaf node?
When the size of the collected elements array path becomes equal to the size of the nums array, it indicates that a full permutation has been found, meaning a leaf node has been reached.
// This means a group has been found
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
2
3
4
5
- Logic of Single Layer Search
Here, the biggest difference from 0077.Combinations (opens new window), 131.Palindrome Partitioning (opens new window), and 78.Subsets (opens new window) is that there's no startIndex in the for loop.
Because in the permutation problem, we have to start searching from the beginning every time, for example, although element 1 was used in [1,2], it has to be used again in [2,1].
And the used array actually records which elements are already used in path, as one element can only be used once in a permutation.
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // Skip elements already included in path
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
2
3
4
5
6
7
8
Complete C++ code is as follows:
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// This means a group has been found
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // Skip elements already included in path
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
- Time Complexity: O(n!)
- Space Complexity: O(n)
# Summary
You can now feel the differences in permutation problems:
- Each level starts the search from 0, not from
startIndex. - A
usedarray is needed to record which elements are already inpath.
Permutation problems are a classic example of problems solved by backtracking algorithms; take some time to understand it.
# Other Language Versions
# Java
class Solution {
List<List<Integer>> result = new ArrayList<>();// Stores the collection of results that meet the condition
LinkedList<Integer> path = new LinkedList<>();// Holds results satisfying the condition
boolean[] used;
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 0){
return result;
}
used = new boolean[nums.length];
permuteHelper(nums);
return result;
}
private void permuteHelper(int[] nums){
if (path.size() == nums.length){
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++){
if (used[i]){
continue;
}
used[i] = true;
path.add(nums[i]);
permuteHelper(nums);
path.removeLast();
used[i] = false;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// Solution 2: Determine already chosen numbers by checking if path contains that number
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
if (nums.length == 0) return result;
backtrack(nums, path);
return result;
}
public void backtrack(int[] nums, LinkedList<Integer> path) {
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
return;
}
for (int i =0; i < nums.length; i++) {
// Skip if path already contains the number
if (path.contains(nums[i])) {
continue;
}
path.add(nums[i]);
backtrack(nums, path);
path.removeLast();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Python
Backtracking with used
class Solution:
def permute(self, nums):
result = []
self.backtracking(nums, [], [False] * len(nums), result)
return result
def backtracking(self, nums, path, used, result):
if len(path) == len(nums):
result.append(path[:])
return
for i in range(len(nums)):
if used[i]:
continue
used[i] = True
path.append(nums[i])
self.backtracking(nums, path, used, result)
path.pop()
used[i] = False
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Go
var (
res [][]int
path []int
st []bool // abbreviation for state
)
func permute(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
st = make([]bool, len(nums))
dfs(nums, 0)
return res
}
func dfs(nums []int, cur int) {
if cur == len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
for i := 0; i < len(nums); i++ {
if !st[i] {
path = append(path, nums[i])
st[i] = true
dfs(nums, cur + 1)
st[i] = false
path = path[:len(path)-1]
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# JavaScript
/**
* @param {number[]} nums
* @return {number[][]}
*/
var permute = function(nums) {
const res = [], path = [];
backtracking(nums, nums.length, []);
return res;
function backtracking(n, k, used) {
if(path.length === k) {
res.push(Array.from(path));
return;
}
for (let i = 0; i < k; i++ ) {
if(used[i]) continue;
path.push(n[i]);
used[i] = true; // same branch
backtracking(n, k, used);
path.pop();
used[i] = false;
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# TypeScript
function permute(nums: number[]): number[][] {
const resArr: number[][] = [];
const helperSet: Set<number> = new Set();
backTracking(nums, []);
return resArr;
function backTracking(nums: number[], route: number[]): void {
if (route.length === nums.length) {
resArr.push([...route]);
return;
}
let tempVal: number;
for (let i = 0, length = nums.length; i < length; i++) {
tempVal = nums[i];
if (!helperSet.has(tempVal)) {
route.push(tempVal);
helperSet.add(tempVal);
backTracking(nums, route);
route.pop();
helperSet.delete(tempVal);
}
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Rust
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, used: &mut Vec<bool>) {
let len = nums.len();
if path.len() == len {
result.push(path.clone());
return;
}
for i in 0..len {
if used[i] == true { continue; }
used[i] = true;
path.push(nums[i]);
Self::backtracking(result, path, nums, used);
path.pop();
used[i] = false;
}
}
pub fn permute(nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut path: Vec<i32> = Vec::new();
let mut used = vec![false; nums.len()];
Self::backtracking(&mut result, &mut path, &nums, &mut used);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# C
int* path;
int pathTop;
int** ans;
int ansTop;
// Set all elements in used to 0
void initialize(int* used, int usedLength) {
int i;
for(i = 0; i < usedLength; i++) {
used[i] = 0;
}
}
// Copy elements from path to ans
void copy() {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int i;
for(i = 0; i < pathTop; i++) {
tempPath[i] = path[i];
}
ans[ansTop++] = tempPath;
}
void backTracking(int* nums, int numsSize, int* used) {
// If the number of elements in path equals the number of elements in nums, put nums in ans
if(pathTop == numsSize) {
copy();
return;
}
int i;
for(i = 0; i < numsSize; i++) {
// Skip current element if it has already been used
if(used[i])
continue;
used[i] = 1;
path[pathTop++] = nums[i];
backTracking(nums, numsSize, used);
// Backtrack
pathTop--;
used[i] = 0;
}
}
int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
// Initialize auxiliary variables
path = (int*)malloc(sizeof(int) * numsSize);
ans = (int**)malloc(sizeof(int*) * 1000);
int* used = (int*)malloc(sizeof(int) * numsSize);
// Set all elements in used to 0
initialize(used, numsSize);
ansTop = pathTop = 0;
backTracking(nums, numsSize, used);
// Set the length of path and ans arrays
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = numsSize;
}
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
# Swift
func permute(_ nums: [Int]) -> [[Int]] {
var result = [[Int]]()
var path = [Int]()
var used = [Bool](repeating: false, count: nums.count) // Records elements already contained in path
func backtracking() {
// Termination condition, gather results
if path.count == nums.count {
result.append(path)
return
}
for i in 0 ..< nums.count {
if used[i] { continue } // Exclude elements already contained
used[i] = true
path.append(nums[i])
backtracking()
// Backtrack
path.removeLast()
used[i] = false
}
}
backtracking()
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Scala
object Solution {
import scala.collection.mutable
def permute(nums: Array[Int]): List[List[Int]] = {
var result = mutable.ListBuffer[List[Int]]()
var path = mutable.ListBuffer[Int]()
def backtracking(used: Array[Boolean]): Unit = {
if (path.size == nums.size) {
// If path's length equals nums, it can be added to the result set
result.append(path.toList)
return
}
// Add loop guard, proceed with backtracking only if current number hasn't been used
for (i <- nums.indices if used(i) == false) {
used(i) = true
path.append(nums(i))
backtracking(used) // Backtrack
path.remove(path.size - 1)
used(i) = false
}
}
backtracking(new Array[Boolean](nums.size)) // Call method
result.toList // Finally return result set in List form
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# C#
public class Solution
{
public IList<IList<int>> res = new List<IList<int>>();
public IList<int> path = new List<int>();
public IList<IList<int>> Permute(int[] nums)
{
var used = new bool[nums.Length];
BackTracking(nums, used);
return res;
}
public void BackTracking(int[] nums, bool[] used)
{
if (path.Count == nums.Length)
{
res.Add(new List<int>(path));
return;
}
for (int i = 0; i < nums.Length; i++)
{
if (used[i]) continue;
used[i] = true;
path.Add(nums[i]);
BackTracking(nums, used);
used[i] = false;
path.RemoveAt(path.Count - 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
