# Problem 77: Combinations
LeetCode Problem Link (opens new window)
Given two integers n and k, return all possible combinations of k numbers out of the range 1 ... n.
Example: Input: n = 4, k = 2 Output: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
# Approach
This is a classic backtracking problem.
A straightforward solution is to use for-loops. For example, when k is 2, we can easily think of using two nested for-loops, which would produce the same output as in the example.
The code is as follows:
int n = 4;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
cout << i << " " << j << endl;
}
}
2
3
4
5
6
Input: n = 100, k = 3 would require three nested for-loops, as follows:
int n = 100;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
for (int u = j + 1; u <= n; n++) {
cout << i << " " << j << " " << u << endl;
}
}
}
2
3
4
5
6
7
8
But what if n is 100 and k is 50? Writing 50 layers of for-loops becomes impractical.
What to do?
Backtracking comes to the rescue. Even though backtracking is also a brute force approach, it is implementable, unlike 50 layers of nested for-loops, which might seem overwhelming.
How does backtracking accomplish this task?
Mentioned earlier, if n is 100 and k is 50, implementing brute force with nested loops is nearly impossible, so backtracking uses recursion to solve the issue of nested loop layers.
Recursion helps handle the layer stacking (think of opening k layers of for-loops). Each recursion nests a for-loop, so recursion can be used to handle the problem of multiple layers.
Here, recursion should have the same number of layers matching the problem, for example, for n = 100 and k = 50, which means 50 recursive layers.
Some might already find recursion confusing, and recursion within backtracking containing a for-loop can be mind-boggling!
Trying to mentally navigate through backtracking might feel suffocating, so abstracting the structure to a tree might make more sense.
In Backtracking Algorithm Fundamentals (opens new window), it was discussed that problems solved with backtracking can be abstracted into tree structures (N-ary trees), allowing backtracking to be understood more easily.
Below is the tree structure abstracted from the combinations problem:
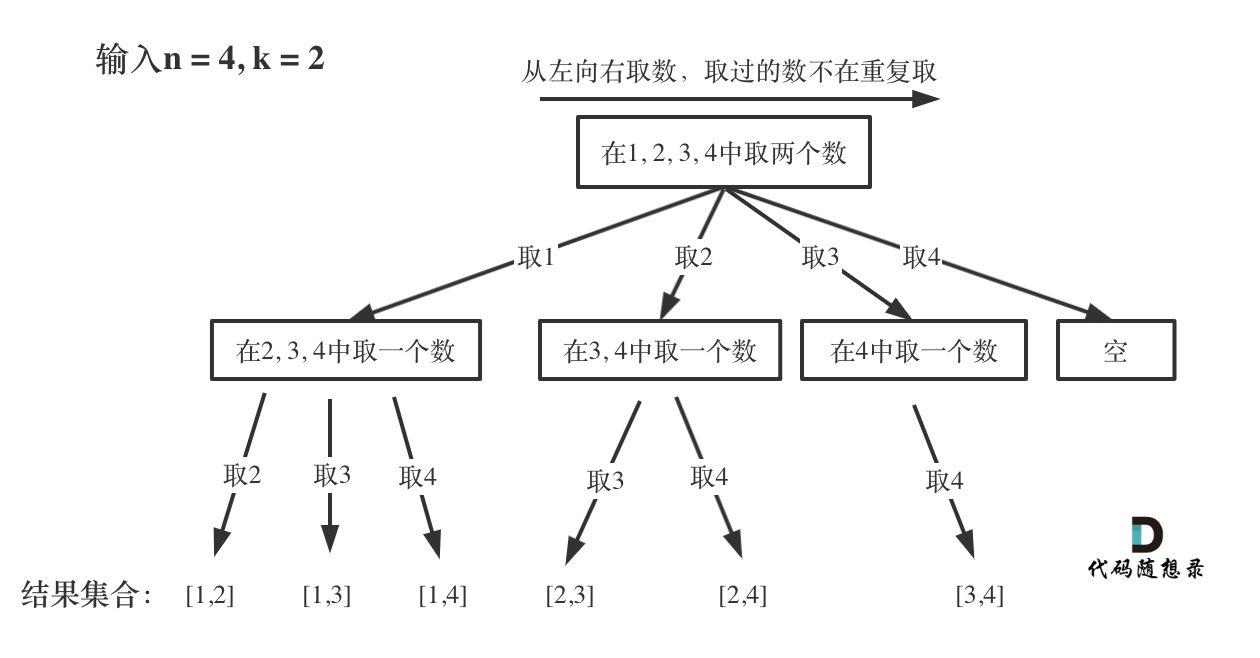
In this tree, initially, the set is {1,2,3,4}, and numbers are chosen from left to right, with already chosen numbers being unavailable for future selection.
The first choice is 1, making the set {2,3,4}; since k is 2, selecting one more number gives combinations [1,2], [1,3], and [1,4], and so on.
With each element selection, the range of selectable elements narrows, effectively adjusting the selectable range.
The diagram shows that n is analogous to the tree's width, and k is analogous to its depth.
The goal is to traverse this tree and collect the results we need.
Every time a leaf node is reached, a result is found.
The red portion in the diagram:
In this context, reaching a leaf node means the result is found, and all that remains is to collect the result at each leaf node.
We emphasized in Backtracking Algorithm Fundamentals (opens new window) that any problem solved using backtracking can be abstracted as a tree structure.
So the path from the root to a leaf should be collected into result across these trees and finally return the combination counting from n to k.
# The Three-Part Backtracking Approach
- Return values and parameters of the recursive function
Here, two global variables must be defined: one for storing each valid result and one for storing the entire set of valid results.
The code looks like this:
vector<vector<int>> result; // For storing the set of valid results
vector<int> path; // For storing a single valid result
2
It's worth noting that excluding these global variables and placing them within the recursive function's parameters would also work, though adding too many parameters might harm readability, which is why I chose to use global variables.
The function must also have two parameters since n and k are integers.
An additional int-type parameter startIndex is also needed to record the set's start position for this recursion level (from the set [1,...,n]).
Why is the startIndex necessary?
Suggested viewing at 07:36 in the 77. Combination Video Explanation (opens new window); the startIndex prevents duplicate combinations.
From the red part in the following diagram, it shows that after selecting 1 from [1,2,3,4], the next recursive step needs to pick numbers from [2,3,4], which the next recursive step inherits from startIndex.
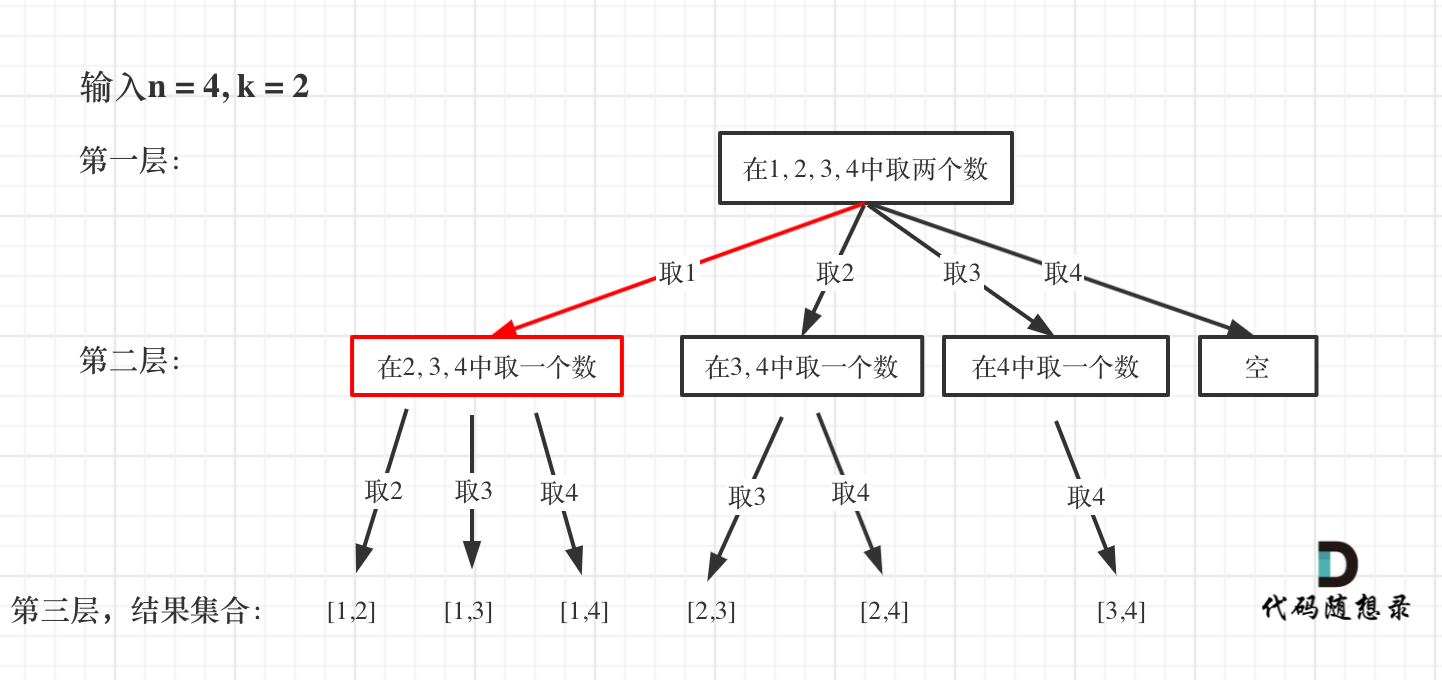
So the startIndex is crucial for recording the search's starting position in the next recursion layer.
The complete code is as follows:
vector<vector<int>> result; // For storing the full set of valid results
vector<int> path; // For storing a single valid result
void backtracking(int n, int k, int startIndex)
2
3
- Termination condition for backtracking
When is the leaf node reached?
If path reaches the size of k, it signifies finding a subset with a size of k. In the diagram, path tells the path from the root to the leaf.
The red portion in the diagram shows:
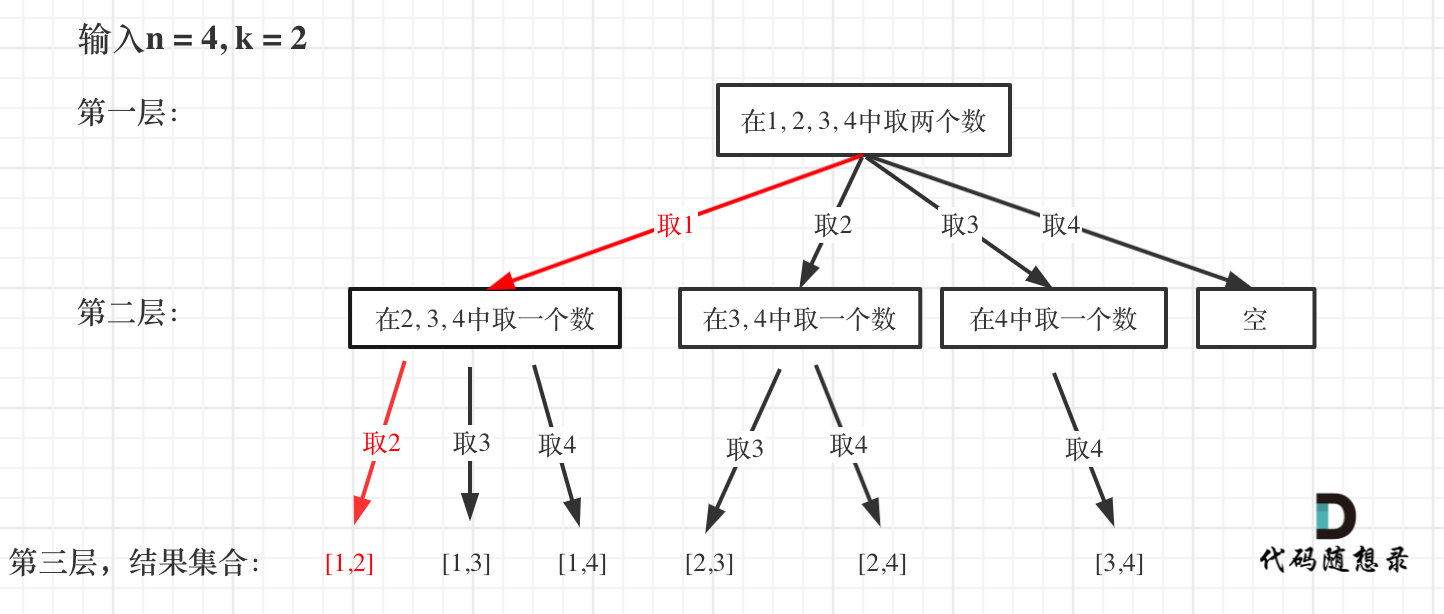
With this, the path, which is the result from the root to the leaf node, should be stored in the result 2D vector and terminate the current recursion.
So the termination condition code looks like this:
if (path.size() == k) {
result.push_back(path);
return;
}
2
3
4
- Process per search level
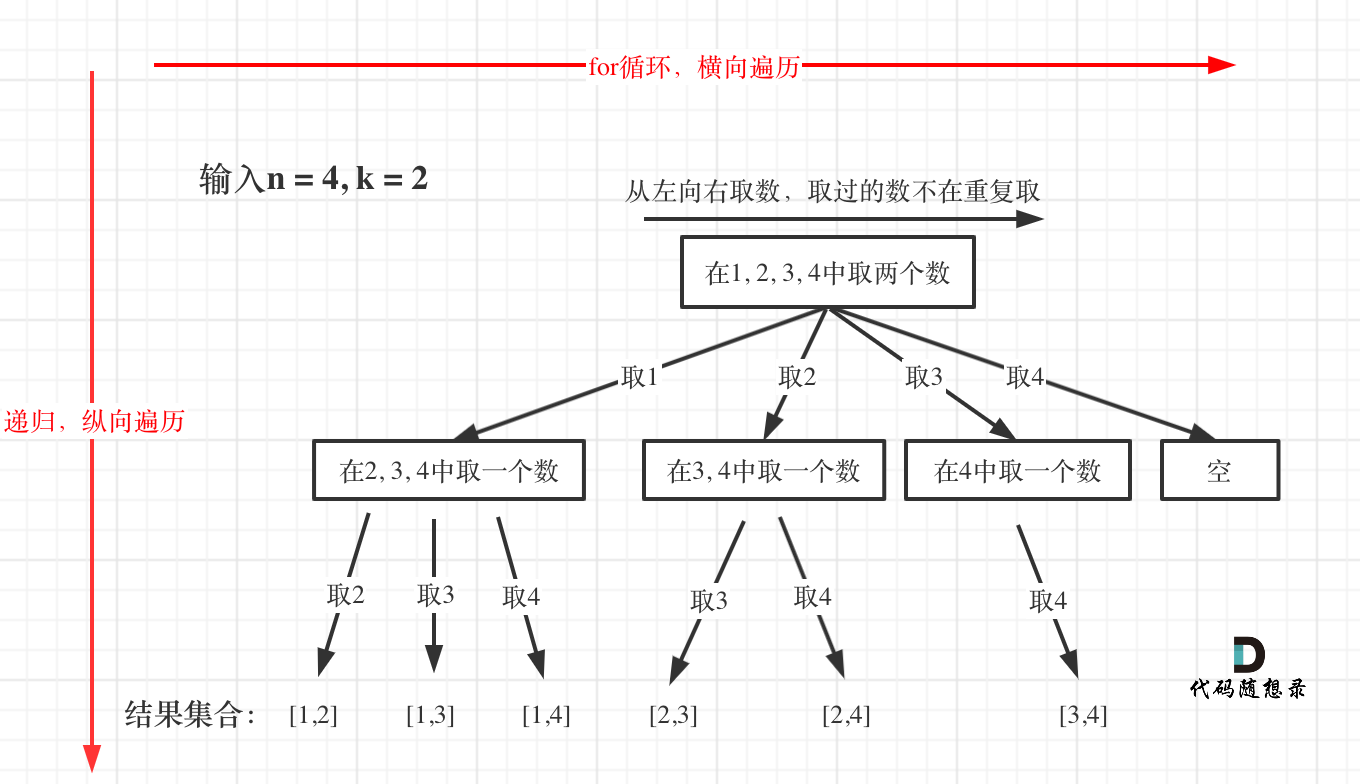
The search process in backtracking is similar to a tree traversal process. From the below diagram, the for-loop is responsible for horizontal traversal, while recursion is responsible for vertical traversal.

Thus the tree can be traversed entirely, exploring all combinations.
The for-loop iterates starting at startIndex each time and uses the path to store the selected node i.
The code is as follows:
for (int i = startIndex; i <= n; i++) { // Controls horizontal tree traversal
path.push_back(i); // Handle node
backtracking(n, k, i + 1); // Recursion: controls vertical traversal, next level search starts from i+1
path.pop_back(); // Backtrack and undo the node handling
}
2
3
4
5
The backtracking (recursive function) keeps calling itself deeper until reaching leaf nodes, where path is collected as a valid result at each.
Below the backtracking function, nodes are retracted at the end through backtracking.
Below is the complete C++ code for the combination problem:
class Solution {
private:
vector<vector<int>> result; // For storing the full set of valid results
vector<int> path; // For storing a single valid result
void backtracking(int n, int k, int startIndex) {
if (path.size() == k) {
result.push_back(path);
return;
}
for (int i = startIndex; i <= n; i++) {
path.push_back(i); // Handle node
backtracking(n, k, i + 1); // Recursion
path.pop_back(); // Backtrack, undo node handling
}
}
public:
vector<vector<int>> combine(int n, int k) {
result.clear(); // Can be omitted
path.clear(); // Can be omitted
backtracking(n, k, 1);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
- Time Complexity: O(n * 2^n)
- Space Complexity: O(n)
Remember the backtracking template we provided in Backtracking Algorithm Fundamentals (opens new window)?
Here it is:
void backtracking(parameters) {
if (termination condition) {
store result;
return;
}
for (choice: current level node's collection (the number of children in a tree node is the size of the collection)) {
handle node;
backtracking(path, choice list); // Recursion
backtrack, undo handling
}
}
2
3
4
5
6
7
8
9
10
11
12
Compare this to the code for this problem—it seems familiar, doesn't it? This template provides a general direction for solving the problem.
# Summary
The combination problem is a classic problem solved with the backtracking approach, initially challenging the idea of implementing a 50-layer loop when n is 100 and k is 50.
This led to the introduction of backtracking, which solves k-layer loop nesting issues.
Visualizing the search process through tree abstraction leads to a clearer understanding.
Following the three-part backtracking approach, the parameters, termination condition, and process per search layer were analyzed, leading to a successful code implementation.
# Pruning Optimization
While backtracking is brute force in essence, there can be some optimization through pruning.
During the traversal process, the following code appears:
for (int i = startIndex; i <= n; i++) {
path.push_back(i);
backtracking(n, k, i + 1);
path.pop_back();
}
2
3
4
5
This traversal range can be optimized—how?
Let's use an example: if n = 4 and k = 4, then in the first layer of for-loop, anything beyond element 2 has no significance. In the second layer, anything beyond element 3 has no relevance.
This explanation might be abstract, so let's see the following graphic:
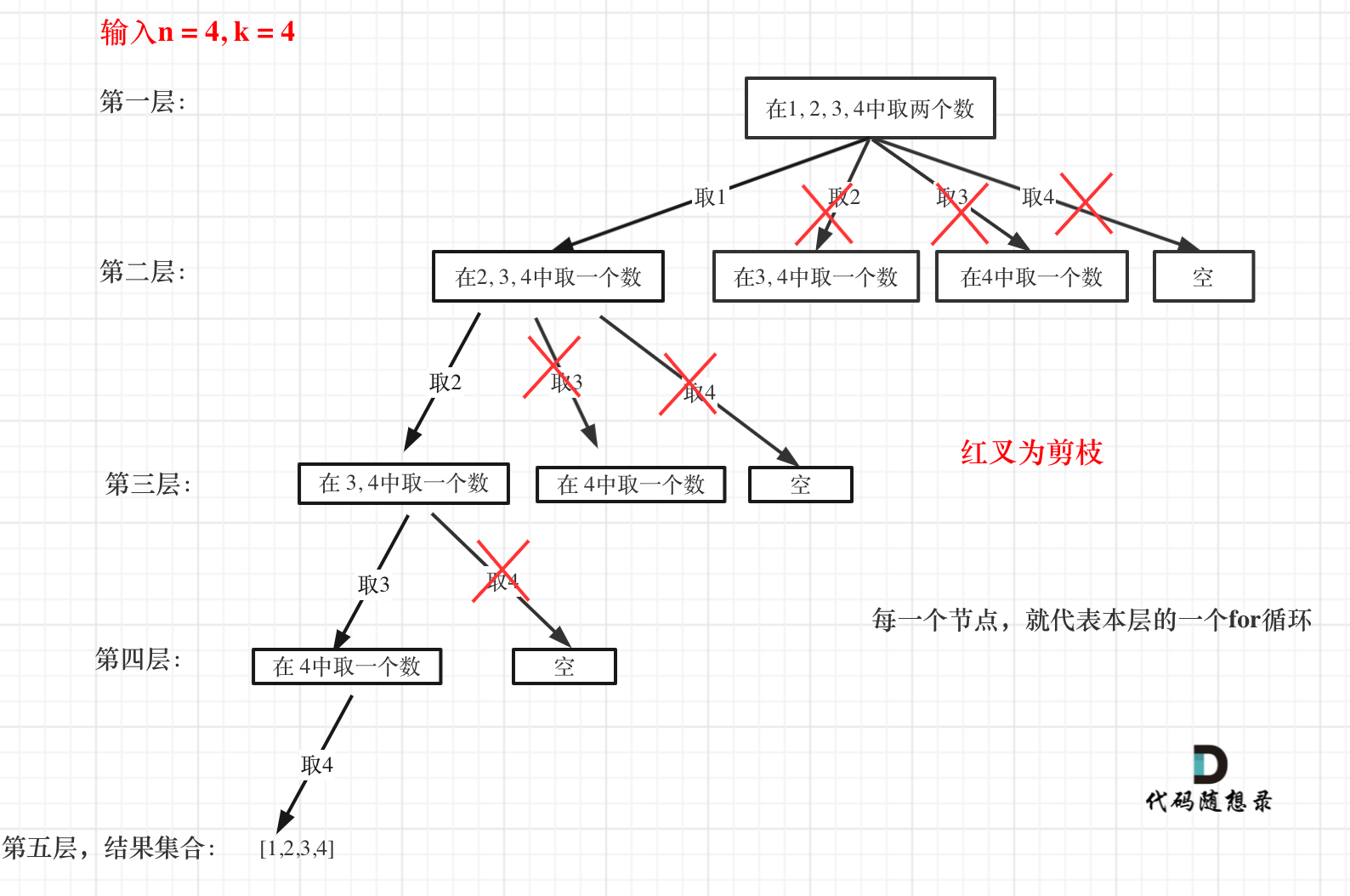
Each node (rectangle in the image) represents a layer in the for-loop. Anything starting in the second node of each layer is invalid, making it an ineffective traversal.
Thus, the critical optimization point lies within each for-loop's starting position across recursion layers.
If the number of subsequent elements from a for-loop start is less than the required elements, then searching further is unnecessary.
Let's explain the optimization process step-by-step:
Number of already selected elements:
path.size();Number of needed elements still:
k - path.size();Starting position for this loop can be determined by:
n - (k - path.size()) + 1.
Notice the +1—this makes the collection [start, end] inclusive.
For example, if n = 4, k = 3, and no elements are yet selected (path.size is 0), the maximum starting point for efficient searching is 4 - (3 - 0) + 1 = 2.
From 2 onwards are reasonable starts, yielding combination[2, 3, 4].
If unsure, try similar examples to clarify.
With these optimizations, the for-loop transforms into:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i signifies the start point for this search
Here is the complete code with optimizations:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(int n, int k, int startIndex) {
if (path.size() == k) {
result.push_back(path);
return;
}
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // Optimized section
path.push_back(i); // Handle node
backtracking(n, k, i + 1);
path.pop_back(); // Backtrack and undo node handling
}
}
public:
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Pruning Summary
In this article, the combination problem's backtracking algorithm implementation was optimized using pruning, which is best understood with visuals, explaining how terms were pruned from the overall search process.
# Other Language Implementations
# Java:
Without pruning:
class Solution {
List<List<Integer>> result= new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
backtracking(n,k,1);
return result;
}
public void backtracking(int n,int k,int startIndex){
if (path.size() == k){
result.add(new ArrayList<>(path));
return;
}
for (int i =startIndex;i<=n;i++){
path.add(i);
backtracking(n,k,i+1);
path.removeLast();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
With pruning:
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
combineHelper(n, k, 1);
return result;
}
/**
* Adjusts selectable range with startIndex
* @param startIndex Traces current level of recursion's index
*/
private void combineHelper(int n, int k, int startIndex){
if (path.size() == k){
result.add(new ArrayList<>(path));
return;
}
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
path.add(i);
combineHelper(n, k, i + 1);
path.removeLast();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Python
Without pruning:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = [] # Store results set
self.backtracking(n, k, 1, [], result)
return result
def backtracking(self, n, k, startIndex, path, result):
if len(path) == k:
result.append(path[:])
return
for i in range(startIndex, n + 1): # Section to optimize
path.append(i) # Handle node
self.backtracking(n, k, i + 1, path, result)
path.pop() # Backtrack and undo node handling
2
3
4
5
6
7
8
9
10
11
12
13
With pruning:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
result = [] # Store results set
self.backtracking(n, k, 1, [], result)
return result
def backtracking(self, n, k, startIndex, path, result):
if len(path) == k:
result.append(path[:])
return
for i in range(startIndex, n - (k - len(path)) + 2): # Optimized section
path.append(i) # Handle node
self.backtracking(n, k, i + 1, path, result)
path.pop() # Backtrack and undo node handling
2
3
4
5
6
7
8
9
10
11
12
13
# Go
var (
path []int
res [][]int
)
func combine(n int, k int) [][]int {
path, res = make([]int, 0, k), make([][]int, 0)
dfs(n, k, 1)
return res
}
func dfs(n int, k int, start int) {
if len(path) == k { // Condition met for k elements
tmp := make([]int, k)
copy(tmp, path)
res = append(res, tmp)
return
}
for i := start; i <= n; i++ { // Starts and avoids duplication
if n - i + 1 < k - len(path) { // Pruning
break
}
path = append(path, i)
dfs(n, k, i+1)
path = path[:len(path)-1]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# JavaScript
Without prunning:
var combine = function (n, k) {
// Backtracking
let result = [],
path = [];
let backtracking = (_n, _k, startIndex) => {
// Termination condition
if (path.length === _k) {
result.push(path.slice());
return;
}
// Loop through current level elements
for (let i = startIndex; i <= _n; i++) {
path.push(i);
// Recursion
backtracking(_n, _k, i + 1);
// Backtracking step
path.pop();
}
};
backtracking(n, k, 1);
return result;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
With pruning:
var combine = function (n, k) {
// Backtracking
let result = [],
path = [];
let backtracking = (_n, _k, startIndex) => {
// Termination condition
if (path.length === _k) {
result.push(path.slice());
return;
}
// Loop through current level elements
for (let i = startIndex; i <= _n - (_k - path.length) + 1; i++) {
path.push(i);
// Recursion
backtracking(_n, _k, i + 1);
// Backtracking step
path.pop();
}
};
backtracking(n, k, 1);
return result;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# TypeScript
function combine(n: number, k: number): number[][] {
let resArr: number[][] = [];
function backTracking(n: number, k: number, startIndex: number, tempArr: number[]): void {
if (tempArr.length === k) {
resArr.push(tempArr.slice());
return;
}
for (let i = startIndex; i <= n - k + 1 + tempArr.length; i++) {
tempArr.push(i);
backTracking(n, k, i + 1, tempArr);
tempArr.pop();
}
}
backTracking(n, k, 1, []);
return resArr;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Rust
Without pruning
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, start_index: i32) {
let len= path.len() as i32;
if len == k{
result.push(path.to_vec());
return;
}
for i in start_index..= n {
path.push(i);
Self::backtracking(result, path, n, k, i+1);
path.pop();
}
}
pub fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {
let mut result = vec![];
let mut path = vec![];
Self::backtracking(&mut result, &mut path, n, k, 1);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
With pruning
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, start_index: i32) {
let len= path.len() as i32;
if len == k{
result.push(path.to_vec());
return;
}
// Pruning done here
for i in start_index..= n - (k - len) + 1 {
path.push(i);
Self::backtracking(result, path, n, k, i+1);
path.pop();
}
}
pub fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {
let mut result = vec![];
let mut path = vec![];
Self::backtracking(&mut result, &mut path, n, k, 1);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C
int* path;
int pathTop;
int** ans;
int ansTop;
void backtracking(int n, int k,int startIndex) {
// Upon reaching path size k, store path in ans 2D array
if(pathTop == k) {
// Create new array to store path as path values change with backtracking
int* temp = (int*)malloc(sizeof(int) * k);
int i;
for(i = 0; i < k; i++) {
temp[i] = path[i];
}
ans[ansTop++] = temp;
return ;
}
int j;
for(j = startIndex; j <=n ;j++) {
// Add current node into path array
path[pathTop++] = j;
// Recursively proceed
backtracking(n, k, j + 1);
// Backtracking, remove top node in array
pathTop--;
}
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
// Path array for storing valid results
path = (int*)malloc(sizeof(int) * k);
// Ans 2D array to store collection of valid results (big enough for extreme cases)
ans = (int**)malloc(sizeof(int*) * 10000);
pathTop = ansTop = 0;
// Backtracking algorithm
backtracking(n, k, 1);
// The final return size is the ans array size
*returnSize = ansTop;
// returnColumnSizes store length of 1D arrays in ans
*returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
int i;
for(i = 0; i < *returnSize; i++) {
(*returnColumnSizes)[i] = k;
}
// Return ans 2D array
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
With pruning:
int* path;
int pathTop;
int** ans;
int ansTop;
void backtracking(int n, int k,int startIndex) {
// When path reaches size of k, store path in ans 2D array
if(pathTop == k) {
// Path array created dynamically, new array needed since path changes with backtracking
int* temp = (int*)malloc(sizeof(int) * k);
int i;
for(i = 0; i < k; i++) {
temp[i] = path[i];
}
ans[ansTop++] = temp;
return ;
}
int j;
for(j = startIndex; j <= n- (k - pathTop) + 1;j++) {
// Handle node by placing into path
path[pathTop++] = j;
// Recursive step
backtracking(n, k, j + 1);
// Backtracking, undo with removing top element
pathTop--;
}
}
int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
// Storage for valid results
path = (int*)malloc(sizeof(int) * k);
// Ans 2D array to store collection (sufficient for edge scenarios)
ans = (int**)malloc(sizeof(int*) * 10000);
pathTop = ansTop = 0;
// Backtracking procedure
backtracking(n, k, 1);
// Output size corresponds to ans array's size
*returnSize = ansTop;
// ReturnColumnSizes are created to highlight ans array lengths which are k
*returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
int i;
for(i = 0; i < *returnSize; i++) {
(*returnColumnSizes)[i] = k;
}
// Return result array
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# Swift
func combine(_ n: Int, _ k: Int) -> [[Int]] {
var path = [Int]()
var result = [[Int]]()
func backtracking(start: Int) {
// For disabling path should collection differ (collected cases also differ)
if path.count == k {
result.append(path)
return
}
// Logic per layer of recursion proceeds
// `let end = n` is overridden
let end = n - (k - path.count) + 1
guard start <= end else { return }
for i in start ... end {
path.append(i) // Handle node
backtracking(start: i + 1) // Recur deeper
path.removeLast() // Remove handled node
}
}
backtracking(start: 1)
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Scala
Without pruning:
object Solution {
import scala.collection.mutable // Import
def combine(n: Int, k: Int): List[List[Int]] = {
var result = mutable.ListBuffer[List[Int]]() // Stores results
var path = mutable.ListBuffer[Int]() // Stores individual results
def backtracking(n: Int, k: Int, startIndex: Int): Unit = {
if (path.size == k) {
// If fulfilled, add to results
result.append(path.toList)
return
}
for (i <- startIndex to n) { // From start index to n
path.append(i) // Temporarily place
backtracking(n, k, i + 1) // Recur deeper
path = path.take(path.size - 1) // Remove handled node
}
}
backtracking(n, k, 1) // Execute backtracking
result.toList // Returns results, omiting return
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
With pruning:
object Solution {
import scala.collection.mutable // Import
def combine(n: Int, k: Int): List[List[Int]] = {
var result = mutable.ListBuffer[List[Int]]() // Glyph stores results
var path = mutable.ListBuffer[Int]() //path stores meaningful counts
def backtracking(n: Int, k: Int, startIndex: Int): Unit = {
if (path.size == k) {
// If fulfilled add to results
result.append(path.toList)
return
}
// Excess loop optimizations follow based on pruning
for (i <- startIndex to (n - (k - path.size) + 1)) {
path.append(i) // Handle node by placing in path
backtracking(n, k, i + 1) // Execute deeper recursion
path = path.take(path.size - 1) // Undo with node removal
}
}
backtracking(n, k, 1) // Execute iterative scheme
result.toList // Eventually returns result set omitting return
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Ruby
def combine(n, k)
result = []
path = []
backtracking(result, path, n, 1, k)
return result
end
# Optimize with pruning
def backtracking(result, path, n, j, k)
if path.size == k
result << path.map {|item| item}
return
end
for i in j..(n-(k - path.size)) + 1
# Handle the node
path << i
backtracking(result, path, n, i + 1, k)
# Backtrack, retract handled node
path.pop
end
end
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# C#
Without pruning:
public class Solution
{
public IList<IList<int>> res = new List<IList<int>>();
public IList<int> path = new List<int>();
public IList<IList<int>> Combine(int n, int k)
{
BackTracking(n, k, 1);
return res;
}
public void BackTracking(int n, int k, int start)
{
if (path.Count == k)
{
res.Add(new List<int>(path));
return;
}
for (int i = start; i <= n; i++)
{
path.Add(i);
BackTracking(n, k, i + 1);
path.RemoveAt(path.Count - 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
With pruning:
public class Solution
{
public IList<IList<int>> res = new List<IList<int>>();
public IList<int> path = new List<int>();
public IList<IList<int>> Combine(int n, int k)
{
BackTracking(n, k, 1);
return res;
}
public void BackTracking(int n, int k, int start)
{
if (path.Count == k)
{
res.Add(new List<int>(path));
return;
}
for (int i = start; i <= n - (k - path.Count) + 1; i++)
{
path.Add(i);
BackTracking(n, k, i + 1);
path.RemoveAt(path.Count - 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
