Similar to the subset problem, but full of pitfalls

491. Non-decreasing Subsequences

LeetCode problem link (opens new window)

Given an integer array, your task is to find all the non-decreasing subsequences of the array. The length of these subsequences must be at least 2.

Example:

• Input: [4, 6, 7, 7]
• Output: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

Note:

• The given array length will not exceed 15.
• The range of integers in the array is [-100, 100].
• The given array might contain duplicate numbers, and equal numbers should be regarded as a non-decreasing sequence.

Thought Process

This problem of finding non-decreasing subsequences is somewhat like taking ordered subsets. Moreover, the problem also requires that there be no duplicate non-decreasing subsequences.

This is very similar to 0090.Subsets II (opens new window) which we discussed earlier.

But precisely because it is so similar, we need to pay attention to the differences, otherwise we might fall into traps!

In 0090.Subsets II (opens new window), we achieved de-duplication through sorting and a marker array.

However, in this problem, we cannot sort the original array to find non-decreasing subsequences because a sorted array would itself be non-decreasing.

So we cannot use the de-duplication logic from before!

The example given in this problem is a sorted array [4, 6, 7, 7], which might mislead people into thinking that the same approach should be used.

For a clear contrast, I'll use the array [4, 7, 6, 7] to illustrate, which can be abstracted into a tree structure as follows:

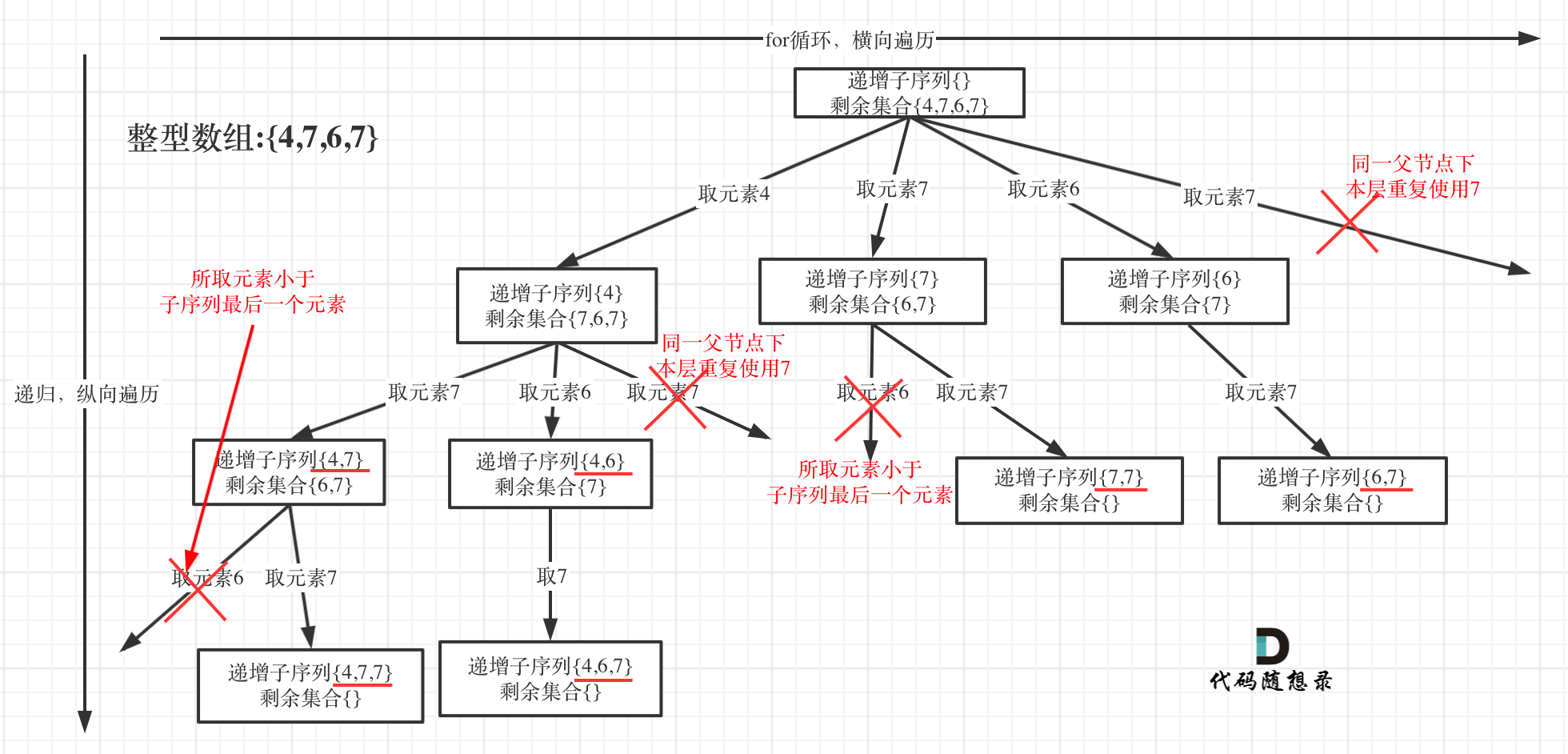
Backtracking in Three Steps

• Parameters for the recursive function

The problem is about finding subsequences, and obviously, an element cannot be reused, so we need startIndex to adjust the starting position for the next layer of recursion.

The code is as follows:

vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex)

• Termination condition

This problem is actually similar to the subset problem, which also needs to traverse the tree to find each node. Thus, similar to 0078.Subsets (opens new window), we can omit a termination condition since startIndex is incremented every time and won't recurse infinitely.

However, this problem has a different requirement for collecting results, as the problem requires non-decreasing subsequences of at least size 2. The code is as follows:

if (path.size() > 1) {
    result.push_back(path);
    // Note not to add 'return' here, as we need to get all nodes on the tree.
}

• Logic for single-layer search

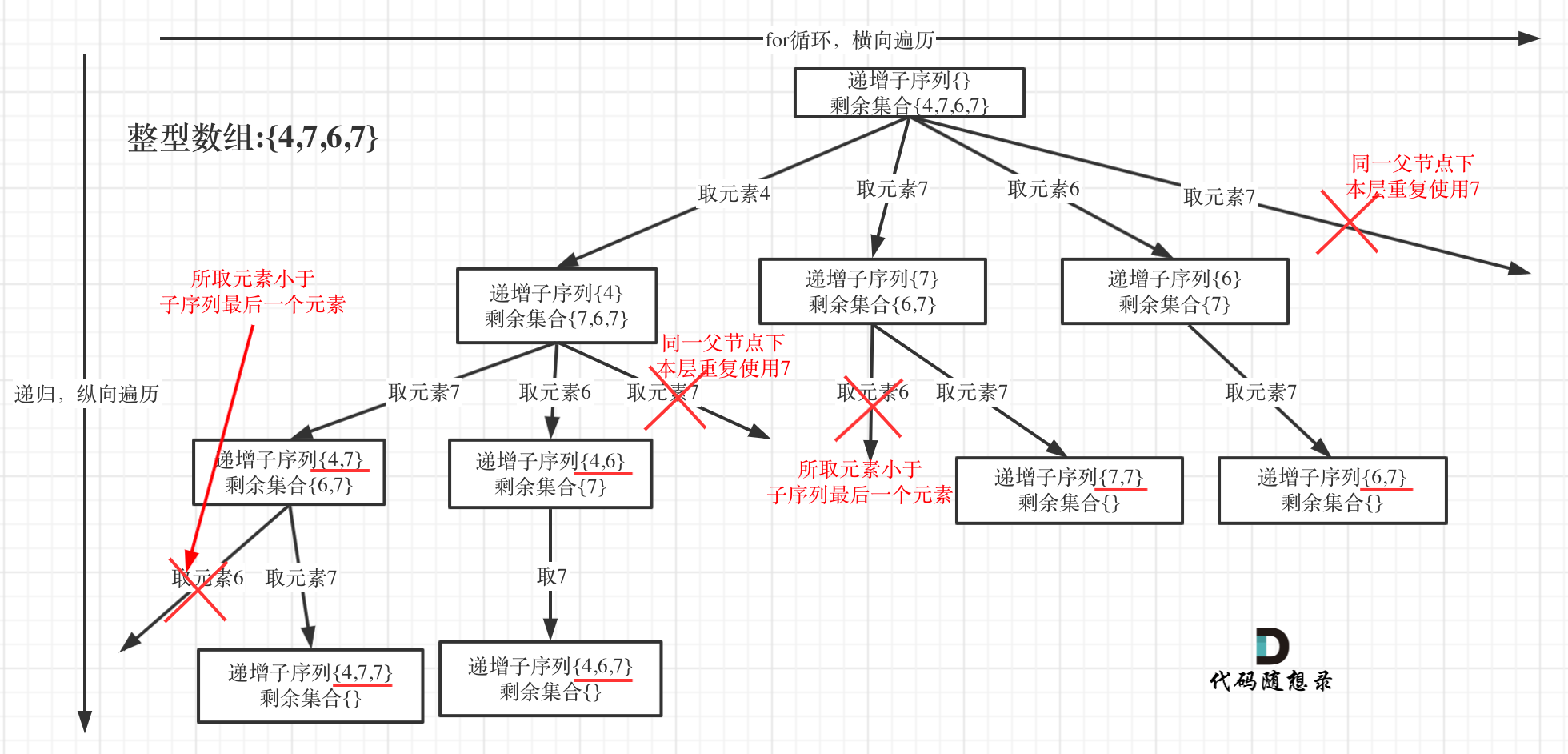
In the figure, it's evident that the same elements at the same level under the same parent node should not be reused.

The single-layer search code is as follows:

unordered_set<int> uset; // Use a set to de-duplicate elements at this level
for (int i = startIndex; i < nums.size(); i++) {
    if ((!path.empty() && nums[i] < path.back())
            || uset.find(nums[i]) != uset.end()) {
            continue;
    }
    uset.insert(nums[i]); // Record that this element has been used at this level
    path.push_back(nums[i]);
    backtracking(nums, i + 1);
    path.pop_back();
}

Those accustomed to writing backtrack algorithms might feel uncomfortable not seeing a corresponding pop operation below uset.insert(nums[i]); in the recursive function.

It's important to note that unordered_set<int> uset; captures repetition at this level only. Each new level redefines (clears) uset, meaning uset only has a scope for that level!

Here is the complete C++ code:

// Version 1
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex) {
        if (path.size() > 1) {
            result.push_back(path);
            // Note not to add 'return', as we need to get all nodes on the tree
        }
        unordered_set<int> uset; // Use set to de-duplicate elements at this level
        for (int i = startIndex; i < nums.size(); i++) {
            if ((!path.empty() && nums[i] < path.back())
                    || uset.find(nums[i]) != uset.end()) {
                    continue;
            }
            uset.insert(nums[i]); // Record that this element has been used at this level
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        result.clear();
        path.clear();
        backtracking(nums, 0);
        return result;
    }
};

• Time Complexity: O(n * 2^n)
• Space Complexity: O(n)

Optimization

In the above code, I used unordered_set<int> to track whether elements at the same level were used.

We can significantly improve efficiency by using an array as a hash map.

Note that the problem stated the number range is [-100,100], so we can use an array for hashing.

When the program runs and unordered_set frequently calls insert, unordered_set needs to hash (map the key to a unique hash value through a hash function), which is relatively time-consuming. Also, redefining a set each time, while inserting causes the underlying symbol table to expand accordingly, making it inefficient.

Here's the optimized code:

// Version 2
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex) {
        if (path.size() > 1) {
            result.push_back(path);
        }
        int used[201] = {0}; // We use an array to handle de-duplication, given the [-100, 100] range
        for (int i = startIndex; i < nums.size(); i++) {
            if ((!path.empty() && nums[i] < path.back())
                    || used[nums[i] + 100] == 1) {
                    continue;
            }
            used[nums[i] + 100] = 1; // Record that this element has been used at this level
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }
public:
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        result.clear();
        path.clear();
        backtracking(nums, 0);
        return result;
    }
};

This version performs much better on LeetCode than version one.

As mentioned in the Hash Table Summary (opens new window), arrays, sets, and maps can all serve as hash tables. If the value range is small, it's best to use arrays.

Summary

While many solutions tag this as depth-first search, I lean towards saying it is tackled using backtracking. In this problem, I have fully utilized backtracking logic.

I believe you see echoes of the 0090.Subsets II (opens new window) solution throughout this problem, yet every step has a set of challenges.

For those getting too familiar with preset patterns or templates, this problem offers an excellent wake-up call, more importantly, it broadens your thought process!

Other Language Versions

Java

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backTracking(nums, 0);
        return result;
    }
    private void backTracking(int[] nums, int startIndex){
        if(path.size() >= 2)
                result.add(new ArrayList<>(path));
        HashSet<Integer> hs = new HashSet<>();
        for(int i = startIndex; i < nums.length; i++){
            if(!path.isEmpty() && path.get(path.size() -1 ) > nums[i] || hs.contains(nums[i]))
                continue;
            hs.add(nums[i]);
            path.add(nums[i]);
            backTracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

class Solution {
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> res = new ArrayList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        backtracking(nums,0);
        return res;
    }

    private void backtracking (int[] nums, int start) {
        if (path.size() > 1) {
            res.add(new ArrayList<>(path));
        }

        int[] used = new int[201];
        for (int i = start; i < nums.length; i++) {
            if (!path.isEmpty() && nums[i] < path.get(path.size() - 1) ||
                    (used[nums[i] + 100] == 1)) continue;
            used[nums[i] + 100] = 1;
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }
}

// Method 2: Using map
class Solution {
    // Result set
    List<List<Integer>> res = new ArrayList<>();
    // Path set
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> findSubsequences(int[] nums) {
        getSubsequences(nums,0);
        return res;
    }
    private void getSubsequences( int[] nums, int start ) {
        if(path.size()>1 ){
            res.add( new ArrayList<>(path) );
            // Note here: don't add return, we need all nodes in the tree
        }
        HashMap<Integer,Integer> map = new HashMap<>();
        for(int i=start ;i < nums.length ;i++){
            if(!path.isEmpty() && nums[i]< path.getLast()){
                continue;
            }
            // Current number already used
            if ( map.getOrDefault( nums[i],0 ) >=1 ){
                continue;
            }
            map.put(nums[i],map.getOrDefault( nums[i],0 )+1);
            path.add( nums[i] );
            getSubsequences( nums,i+1 );
            path.removeLast();
        }
    }
}

Python

Backtracking with set de-duplication

class Solution:
    def findSubsequences(self, nums):
        result = []
        path = []
        self.backtracking(nums, 0, path, result)
        return result
    
    def backtracking(self, nums, startIndex, path, result):
        if len(path) > 1:
            result.append(path[:])  # Use slices for a copy of the current path to append to result set
            # Note don't add return here, as we need to collect all nodes on the tree
        
        uset = set()  # Use a set to de-duplicate elements at this level
        for i in range(startIndex, len(nums)):
            if (path and nums[i] < path[-1]) or nums[i] in uset:
                continue
            
            uset.add(nums[i])  # Record this element as used at this level
            path.append(nums[i])
            self.backtracking(nums, i + 1, path, result)
            path.pop()

Backtracking with hash table de-duplication

class Solution:
    def findSubsequences(self, nums):
        result = []
        path = []
        self.backtracking(nums, 0, path, result)
        return result

    def backtracking(self, nums, startIndex, path, result):
        if len(path) > 1:
            result.append(path[:])  # Use slices for a copy of the current path to append to result set
        
        used = [0] * 201  # Use an array for de-duplication, based on the problem's number range [-100, 100]
        for i in range(startIndex, len(nums)):
            if (path and nums[i] < path[-1]) or used[nums[i] + 100] == 1:
                continue  # If the current element is smaller than the last one in the path, or already used, skip it
            
            used[nums[i] + 100] = 1  # Mark the current element as used
            path.append(nums[i])  # Append the current element into the current non-decreasing subsequence
            self.backtracking(nums, i + 1, path, result)
            path.pop()

Go

var (
    res [][]int
    path  []int
)
func findSubsequences(nums []int) [][]int {
    res, path = make([][]int, 0), make([]int, 0, len(nums))
    dfs(nums, 0)
    return res
}
func dfs(nums []int, start int) {
    if len(path) >= 2 {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
    }
    used := make(map[int]bool, len(nums))   // Initialize a used map for level de-duplication
    for i := start; i < len(nums); i++ {
        if used[nums[i]] {   // De-duplication
            continue
        }
        if len(path) == 0 || nums[i] >= path[len(path)-1] {
            path = append(path, nums[i])
            used[nums[i]] = true
            dfs(nums, i+1)
            path = path[:len(path)-1]
        }
    }
}

JavaScript

var findSubsequences = function(nums) {
    let result = []
    let path = []
    function backtracing(startIndex) {
        if(path.length > 1) {
            result.push(path.slice())
        }
        let uset = []
        for(let i = startIndex; i < nums.length; i++) {
            if((path.length > 0 && nums[i] < path[path.length - 1]) || uset[nums[i] + 100]) {
                continue
            }
            uset[nums[i] + 100] = true
            path.push(nums[i])
            backtracing(i + 1)
            path.pop()
        }
    }
    backtracing(0)
    return result
};

TypeScript

function findSubsequences(nums: number[]): number[][] {
    const resArr: number[][] = [];
    backTracking(nums, 0, []);
    return resArr;
    function backTracking(nums: number[], startIndex: number, route: number[]): void {
        let length: number = nums.length;
        if (route.length >= 2) {
            resArr.push(route.slice());
        }
        const usedSet: Set<number> = new Set();
        for (let i = startIndex; i < length; i++) {
            if (
                nums[i] < route[route.length - 1] ||
                usedSet.has(nums[i])
            ) continue;
            usedSet.add(nums[i]);
            route.push(nums[i]);
            backTracking(nums, i + 1, route);
            route.pop();
        }
    }
};

Rust

Backtracking with hash

use std::collections::HashSet;
impl Solution {
    fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, start_index: usize) {
        if path.len() > 1 { result.push(path.clone()); }
        let len = nums.len();
        let mut uset: HashSet<i32> = HashSet::new();
        for i in start_index..len {
            if (!path.is_empty() && nums[i] < *path.last().unwrap()) || uset.contains(&nums[i]) { continue; }
            uset.insert(nums[i]);
            path.push(nums[i]);
            Solution::backtracking(result, path, nums, i + 1);
            path.pop();
        }
    }

    pub fn find_subsequences(nums: Vec<i32>) -> Vec<Vec<i32>> {
        let mut result: Vec<Vec<i32>> = Vec::new();
        let mut path: Vec<i32> = Vec::new();
        Solution::backtracking(&mut result, &mut path, &nums, 0);
        result
    }
}

Backtracking with array

impl Solution {
    fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, start_index: usize) {
        if path.len() > 1 { result.push(path.clone()); }
        let len = nums.len();
        let mut used = [0; 201];
        for i in start_index..len {
            if (!path.is_empty() && nums[i] < *path.last().unwrap()) || used[(nums[i] + 100) as usize] == 1 { continue; }
            used[(nums[i] + 100) as usize] = 1;
            path.push(nums[i]);
            Solution::backtracking(result, path, nums, i + 1);
            path.pop();
        }
    }

    pub fn find_subsequences(nums: Vec<i32>) -> Vec<Vec<i32>> {
        let mut result: Vec<Vec<i32>> = Vec::new();
        let mut path: Vec<i32> = Vec::new();
        Solution::backtracking(&mut result, &mut path, &nums, 0);
        result
    }
}

C

int* path;
int pathTop;
int** ans;
int ansTop;
int* length;
// Copies the current path content into ans
void copy() {
    int* tempPath = (int*)malloc(sizeof(int) * pathTop);
    memcpy(tempPath, path, pathTop * sizeof(int));
    length[ansTop] = pathTop;
    ans[ansTop++] = tempPath;
}

// Searches if a value exists in uset
int find(int* uset, int usetSize, int key) {
    int i;
    for(i = 0; i < usetSize; i++) {
        if(uset[i] == key)
            return 1;
    }
    return 0;
}

void backTracking(int* nums, int numsSize, int startIndex) {
    // Add path to ans if more than one element is present
    if(pathTop > 1) {
        copy();
    }
    int* uset = (int*)malloc(sizeof(int) * numsSize);
    int usetTop = 0;
    int i;
    for(i = startIndex; i < numsSize; i++) {
        // Skip if current element is smaller than last one in path or already used in the same tree layer
        if((pathTop > 0 && nums[i] < path[pathTop - 1]) || find(uset, usetTop, nums[i]))
            continue;
        // Add current element to uset
        uset[usetTop++] = nums[i];
        // Add current element to path
        path[pathTop++] = nums[i];
        backTracking(nums, numsSize, i + 1);
        // Backtrack
        pathTop--;
    }
}

int** findSubsequences(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    // Initialize auxiliary arrays
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(sizeof(int*) * 33000);
    length = (int*)malloc(sizeof(int*) * 33000);
    pathTop = ansTop = 0;

    backTracking(nums, numsSize, 0);

    // Set the number of elements to return and each 1D array length
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = length[i];
    }
    return ans;
}

Swift

func findSubsequences(_ nums: [Int]) -> [[Int]] {
    var result = [[Int]]()
    var path = [Int]()
    func backtracking(startIndex: Int) {
        // Collect results but do not return, as further concatenation is needed
        if path.count > 1 {
            result.append(path)
        }

        var uset = Set<Int>()
        let end = nums.count
        guard startIndex < end else { return } // Termination condition
        for i in startIndex ..< end {
            let num = nums[i]
            if uset.contains(num) { continue } // Skip duplicate elements
            if !path.isEmpty, num < path.last! { continue } // Ensure increment
            uset.insert(num) // Record using set
            path.append(num) // Process: collect elements
            backtracking(startIndex: i + 1) // Avoid duplicating visits of elements
            path.removeLast() // Backtrack
        }
    }
    backtracking(startIndex: 0)
    return result
}

Scala

object Solution {
  import scala.collection.mutable
  def findSubsequences(nums: Array[Int]): List[List[Int]] = {
    var result = mutable.ListBuffer[List[Int]]()
    var path = mutable.ListBuffer[Int]()

    def backtracking(startIndex: Int): Unit = {
      // If more than one element, add to result set
      if (path.size > 1) {
        result.append(path.toList)
      }

      var used = new Array[Boolean](201)
      // In the current loop, only unvisited elements can enter backtracking
      for (i <- startIndex until nums.size if !used(nums(i) + 100)) {
        // If the path has no elements or the current iteration element is greater than the last in the path, it can backtrack
        if (path.size == 0 || (!path.isEmpty && nums(i) >= path(path.size - 1))) {
          used(nums(i) + 100) = true
          path.append(nums(i))
          backtracking(i + 1)
          path.remove(path.size - 1)
        }
      }
    }

    backtracking(0)
    result.toList
  }
}

C#

public class Solution {
    public IList<IList<int>> res = new List<IList<int>>();
    public IList<int> path = new List<int>();
    public IList<IList<int>> FindSubsequences(int[] nums) {
        BackTracking(nums, 0);
        return res;
    }
    public void BackTracking(int[] nums, int start){
        if(path.Count >= 2){
            res.Add(new List<int>(path));
        }
        HashSet<int> hs = new HashSet<int>();
        for(int i = start; i < nums.Length; i++){
            if(path.Count > 0 && path[path.Count - 1] > nums[i] || hs.Contains(nums[i])){
                continue;
            }
            hs.Add(nums[i]);
            path.Add(nums[i]);
            BackTracking(nums, i + 1);
            path.RemoveAt(path.Count - 1);
        }
    }
}