If you are still unsure about the theory behind backtracking, you can watch this video for a detailed explanation: Here comes the video! Learn Backtracking Algorithm (Theory part) (opens new window)

37. Sudoku Solver

LeetCode Problem Link (opens new window)

Write a program to solve a Sudoku puzzle by filling the empty cells.

A Sudoku solution must satisfy the following rules:

• Each of the digits 1-9 must occur exactly once in each row.
• Each of the digits 1-9 must occur exactly once in each column.
• Each of the digits 1-9 must occur exactly once in each of the 3x3 sub-boxes of the grid.

Empty cells are indicated by the character '.'.

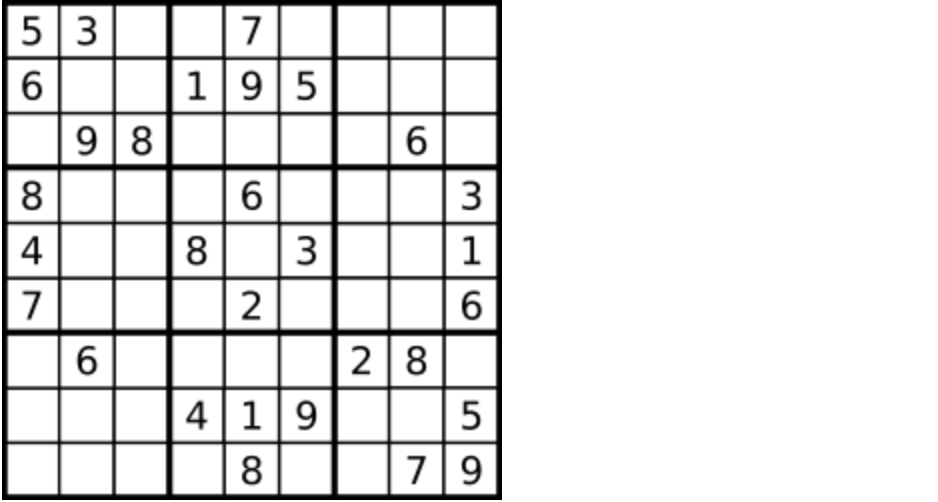
A Sudoku.

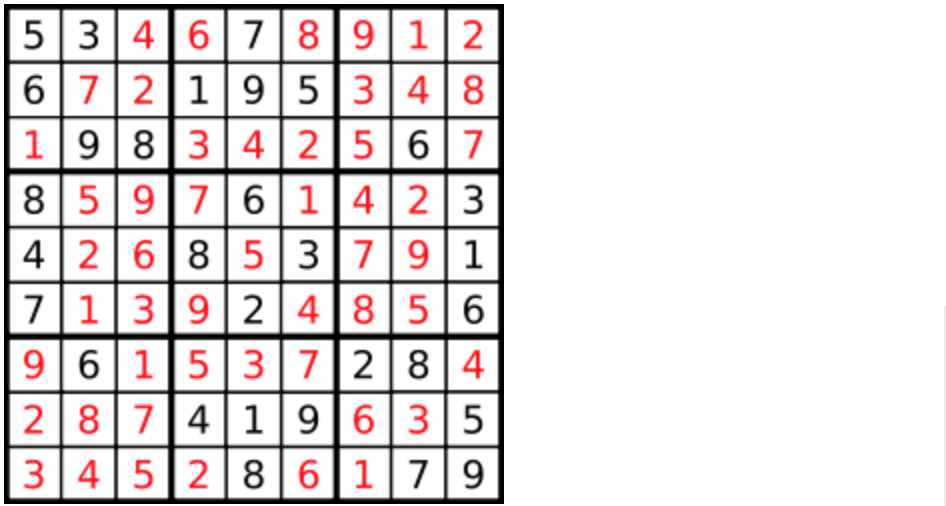
The solution is marked in red.

Constraints:

• The given board contains only the digits 1-9 and the character '.'.
• It is guaranteed that there will be only one unique solution for the given Sudoku.
• The given Sudoku board is always a 9x9 grid.

Approach

Chessboard search problems can be addressed using backtracking techniques by brute-force search; however, this time, we need to perform 2D recursion.

How do we perform 2D recursion?

Those who have followed the "Carl's Coding Garden Path" would have solved one-dimensional recursion problems such as: 0077.Combinations (opens new window), 0131.Palindrome Partitioning (opens new window), 0078.Subsets (opens new window), 0046.Permutations (opens new window), and 0051.N-Queens (opens new window). These problems involve one-dimensional recursion.

If you haven't solved the aforementioned problems, it's not advisable to jump into this problem immediately!

The N-Queens (opens new window) problem requires placing a queen in each row of the chessboard. This can be addressed with a layer of for-loops traversing the rows and recursion handling the columns, where each row and column determines the unique position of the queen.

This problem is different. In this problem, an entire number (compared to N-Queens' one per row) must be placed in every cell a number and verify the validity of those numbers. Therefore, the tree-like structure of solving Sudoku is both broader and deeper than the N-Queens problem.

The complexity of this problem's tree-like structure could be visualized as follows:

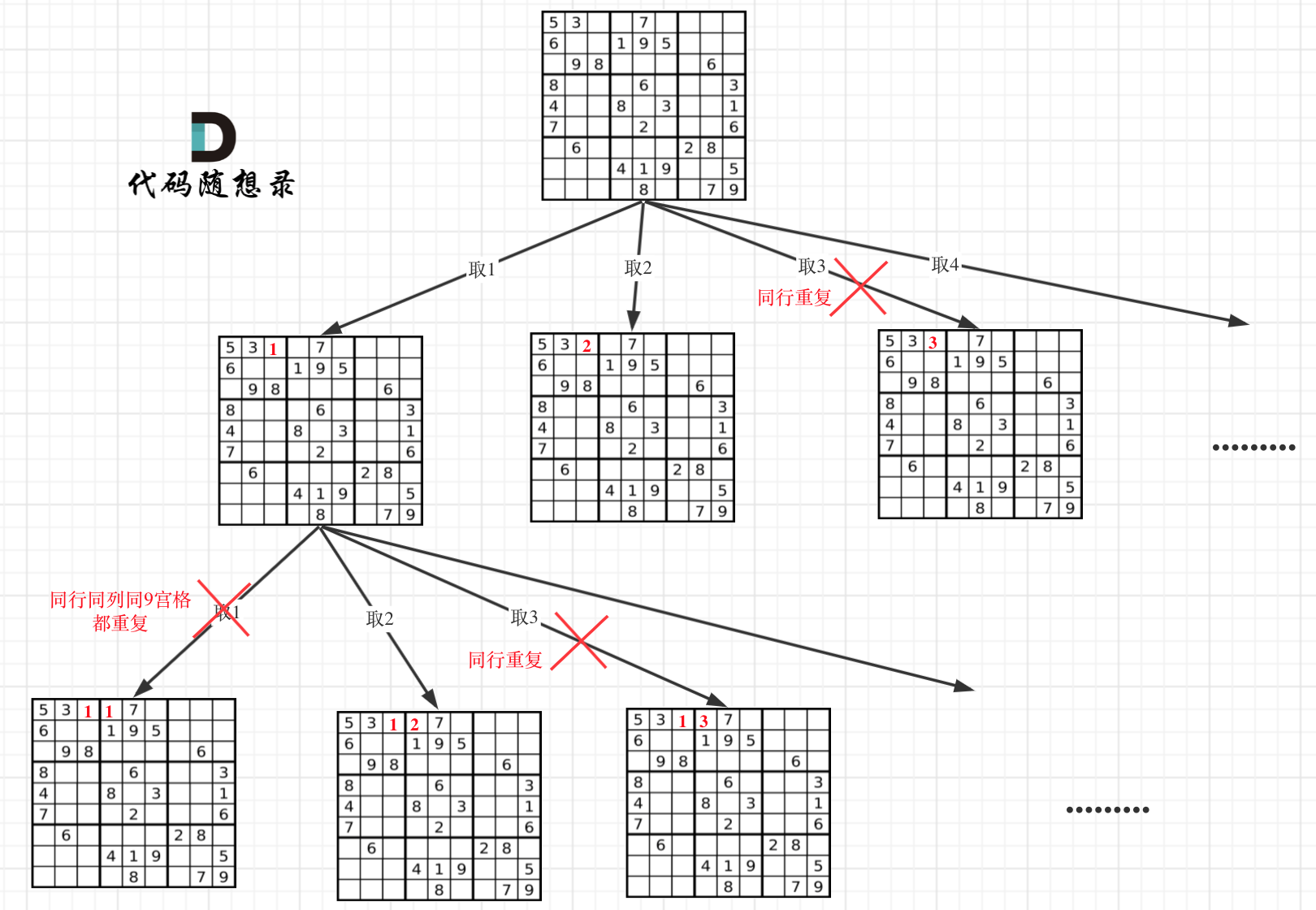
Three Steps of Backtracking

• Recursive Function and Parameters

The return value of the recursive function should be a boolean type; why is that?

The solution for Sudoku can be found once a valid configuration is reached (which is the leaf node in the tree). So, we must return immediately upon finding the solution, which can be seen as finding a single path from the tree root to a leaf, necessitating a boolean return value.

The code is as follows:

bool backtracking(vector<vector<char>>& board)

• Recursive Termination Condition

This time, recursion doesn't require a termination condition as we’re continuously seeking and examining every potential leaf in the tree structure for a valid answer on the Sudoku board.

Would a lack of termination conditions lead to infinite recursion?

Each recursive layer ensures that a new number is added to the board compared to the previous layer. Once the board is filled, recursion naturally terminates — that would indicate that a solution was found. Therefore, a termination condition isn't necessary!

But is there a situation where the board will never be fully filled?

This question will be addressed within the single-layer recursive search logic explanation!

• Single-layer Recursive Search Logic

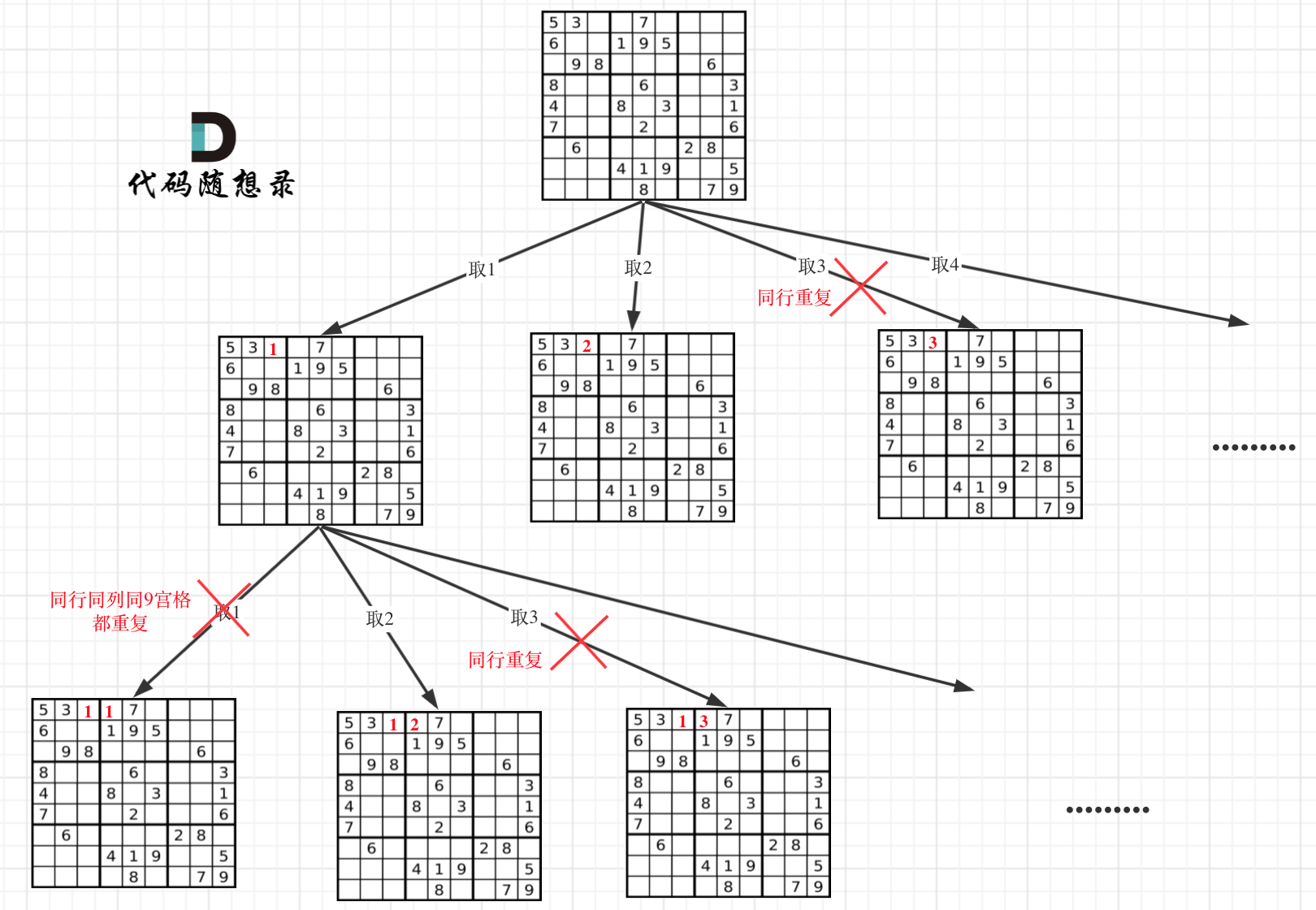
In the tree-structured figure, we can identify the need for a two-dimensional recursive function (both rows and columns).

One for-loop traverses the rows of the board; another one traverses the columns. Once a row and a column are determined, the recursion explores each of the nine possible numbers at that position!

Below is the corresponding code (refer to the comments for details):

bool backtracking(vector<vector<char>>& board) {
    for (int i = 0; i < board.size(); i++) {        // Traverse rows
        for (int j = 0; j < board[0].size(); j++) { // Traverse columns
            if (board[i][j] != '.') continue;
            for (char k = '1'; k <= '9'; k++) {     // Check if 'k' fits at position (i, j)
                if (isValid(i, j, k, board)) {
                    board[i][j] = k;                // Place 'k'
                    if (backtracking(board)) return true; // If a valid solution is found, return immediately
                    board[i][j] = '.';              // Backtrack, undo 'k'
                }
            }
            return false;                           // If all numbers are tried and failed, backtrack and return false
        }
    }
    return true; // If walk-through finishes without returning false, a valid configuration is found
}

Note the placement of the return false here; it is placed based on specific reasoning.

If a row-column coordinate is determined but none of the nine numbers work, it implies this configuration doesn't lead to a solution for this Sudoku. Therefore, it should immediately backtrack — this is also why infinite recursion won't occur since none of the search trees would lead to a solution path!

Determine Whether the Board is Valid

Determining whether a board is valid can be checked through three dimensions:

• Check if any duplicates exist in the same row.
• Check if any duplicates exist in the same column.
• Check if any duplicates exist within the 3x3 sub-grid.

The code is as follows:

bool isValid(int row, int col, char val, vector<vector<char>>& board) {
    for (int i = 0; i < 9; i++) { // Check if any duplicates exist in the row
        if (board[row][i] == val) {
            return false;
        }
    }
    for (int j = 0; j < 9; j++) { // Check if any duplicates exist in the column
        if (board[j][col] == val) {
            return false;
        }
    }
    int startRow = (row / 3) * 3;
    int startCol = (col / 3) * 3;
    for (int i = startRow; i < startRow + 3; i++) { // Check if any duplicates exist in the 3x3 sub-grid
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == val ) {
                return false;
            }
        }
    }
    return true;
}

Here is the complete C++ code:

class Solution {
private:
bool backtracking(vector<vector<char>>& board) {
    for (int i = 0; i < board.size(); i++) {        // Traverse rows
        for (int j = 0; j < board[0].size(); j++) { // Traverse columns
            if (board[i][j] == '.') {
                for (char k = '1'; k <= '9'; k++) { // Check if 'k' absolutely fits in cell (i, j)
                    if (isValid(i, j, k, board)) {
                        board[i][j] = k;           // Place 'k'
                        if (backtracking(board)) return true; // Return immediately if a valid configuration is found
                        board[i][j] = '.';         // Backtrack to undo 'k'
                    }
                }
                return false;  // If all numbers are tried and failed, return false
            }
        }
    }
    return true; // If no 'false' is returned during traversal, a valid configuration is found
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
    for (int i = 0; i < 9; i++) { // Check if any duplicates exist in the row
        if (board[row][i] == val) {
            return false;
        }
    }
    for (int j = 0; j < 9; j++) { // Check if any duplicates exist in the column
        if (board[j][col] == val) {
            return false;
        }
    }
    int startRow = (row / 3) * 3;
    int startCol = (col / 3) * 3;
    for (int i = startRow; i < startRow + 3; i++) { // Check if any duplicates exist in the 3x3 sub-grid
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == val ) {
                return false;
            }
        }
    }
    return true;
}
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};

Conclusion

The Sudoku Solver is an exceedingly difficult problem. When one is stuck in the logic of single-layer recursion, this problem can feel overwhelming.

In my introduction, I emphasized 2D recursion, a self-coined term aimed at assisting you in understanding the Sudoku search process.

Upon thorough analysis, you'll find that the implementation is not overly complex. The challenge lies in grasping the thought process behind 2D recursion.

In this manner, we have conquered such a challenging problem as the Sudoku Solver.

Congratulations to all the coding enthusiasts who persisted all along; the backtracking algorithm is nearing its conclusion, and up next will be a summary.

Solutions in Other Languages

Java

First Solution:

class Solution {
    public void solveSudoku(char[][] board) {
        solveSudokuHelper(board);
    }

    private boolean solveSudokuHelper(char[][] board){
        for (int i = 0; i < 9; i++){ // Traverse rows
            for (int j = 0; j < 9; j++){ // Traverse columns
                if (board[i][j] != '.'){ // Skip original numbers
                    continue;
                }
                for (char k = '1'; k <= '9'; k++){ // Check if 'k' fits in position (i, j)
                    if (isValidSudoku(i, j, k, board)){
                        board[i][j] = k;
                        if (solveSudokuHelper(board)){ // Find a suitable set and return immediately
                            return true;
                        }
                        board[i][j] = '.';
                    }
                }
                return false; // All numbers tried, none succeeded, return false
            }
        }
        return true; // If no false is returned during recursion, a valid configuration was found
    }

    private boolean isValidSudoku(int row, int col, char val, char[][] board){
        for (int i = 0; i < 9; i++){ // Check if any duplicates exist in the row
            if (board[row][i] == val){
                return false;
            }
        }
        for (int j = 0; j < 9; j++){ // Check if any duplicates exist in the column
            if (board[j][col] == val){
                return false;
            }
        }
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++){ // Check 3x3 sub-grid for duplicates
            for (int j = startCol; j < startCol + 3; j++){
                if (board[i][j] == val){
                    return false;
                }
            }
        }
        return true;
    }
}

Second Solution (using bitmap marking):

class Solution{
    int[] rowBit = new int[9];
    int[] colBit = new int[9];
    int[] square9Bit = new int[9];

    public void solveSudoku(char[][] board) {
        for (int y = 0; y < board.length; y++) {
            for (int x = 0; x < board[y].length; x++) {
                int numBit = 1 << (board[y][x] - '1');
                rowBit[y] ^= numBit;
                colBit[x] ^= numBit;
                square9Bit[(y / 3) * 3 + x / 3] ^= numBit;
            }
        }
        backtrack(board, 0);
    }

    public boolean backtrack(char[][] board, int n) {
        if (n >= 81) {
            return true;
        }
        int row = n / 9;
        int col = n % 9;
        if (board[row][col] != '.') {
            return backtrack(board, n + 1);
        }

        for (char c = '1'; c <= '9'; c++) {
            int numBit = 1 << (c - '1');
            if (!isValid(numBit, row, col)) continue;
            {
                board[row][col] = c; 
                rowBit[row] ^= numBit;
                colBit[col] ^= numBit;
                square9Bit[(row / 3) * 3 + col / 3] ^= numBit;
            }
            if (backtrack(board, n + 1)) return true;
            {
                board[row][col] = '.';
                rowBit[row] &= ~numBit; 
                colBit[col] &= ~numBit;
                square9Bit[(row / 3) * 3 + col / 3] &= ~numBit;
            }
        }
        return false;
    }

    boolean isValid(int numBit, int row, int col) {
        if ((rowBit[row] & numBit) > 0) return false;
        if ((colBit[col] & numBit) > 0) return false;
        if ((square9Bit[(row / 3) * 3 + col / 3] & numBit) > 0) return false;
        return true;
    }
}

Python

class Solution:
    def solveSudoku(self, board: List[List[str]]) -> None:
        row_used = [set() for _ in range(9)]
        col_used = [set() for _ in range(9)]
        box_used = [set() for _ in range(9)]
        for row in range(9):
            for col in range(9):
                num = board[row][col]
                if num == ".":
                    continue
                row_used[row].add(num)
                col_used[col].add(num)
                box_used[(row // 3) * 3 + col // 3].add(num)
        self.backtracking(0, 0, board, row_used, col_used, box_used)

    def backtracking(
        self,
        row: int,
        col: int,
        board: List[List[str]],
        row_used: List[List[int]],
        col_used: List[List[int]],
        box_used: List[List[int]],
    ) -> bool:
        if row == 9:
            return True

        next_row, next_col = (row, col + 1) if col < 8 else (row + 1, 0)
        if board[row][col] != ".":
            return self.backtracking(
                next_row, next_col, board, row_used, col_used, box_used
            )

        for num in map(str, range(1, 10)):
            if (
                num not in row_used[row]
                and num not in col_used[col]
                and num not in box_used[(row // 3) * 3 + col // 3]
            ):
                board[row][col] = num
                row_used[row].add(num)
                col_used[col].add(num)
                box_used[(row // 3) * 3 + col // 3].add(num)
                if self.backtracking(
                    next_row, next_col, board, row_used, col_used, box_used
                ):
                    return True
                board[row][col] = "."
                row_used[row].remove(num)
                col_used[col].remove(num)
                box_used[(row // 3) * 3 + col // 3].remove(num)
        return False

Go

func solveSudoku(board [][]byte) {
    var backtracking func(board [][]byte) bool
    backtracking = func(board [][]byte) bool {
        for i := 0; i < 9; i++ {
            for j := 0; j < 9; j++ {
                if board[i][j] != '.' {
                    continue
                }
                for k := '1'; k <= '9'; k++ {
                    if isvalid(i, j, byte(k), board) {
                        board[i][j] = byte(k)
                        if backtracking(board) {
                            return true
                        }
                        board[i][j] = '.'
                    }
                }
                return false
            }
        }
        return true
    }
    backtracking(board)
}

func isvalid(row, col int, k byte, board [][]byte) bool {
    for i := 0; i < 9; i++ {
        if board[row][i] == k {
            return false
        }
    }
    for i := 0; i < 9; i++ {
        if board[i][col] == k {
            return false
        }
    }
    startrow := (row / 3) * 3
    startcol := (col / 3) * 3
    for i := startrow; i < startrow+3; i++ {
        for j := startcol; j < startcol+3; j++ {
            if board[i][j] == k {
                return false
            }
        }
    }
    return true
}

JavaScript

var solveSudoku = function(board) {
    function isValid(row, col, val, board) {
        let len = board.length
        for(let i = 0; i < len; i++) {
            if(board[row][i] === val) {
                return false
            }
        }
        for(let i = 0; i < len; i++) {
            if(board[i][col] === val) {
                return false
            }
        }
        let startRow = Math.floor(row / 3) * 3
        let startCol = Math.floor(col / 3) * 3

        for(let i = startRow; i < startRow + 3; i++) {
            for(let j = startCol; j < startCol + 3; j++) {
                if(board[i][j] === val) {
                    return false
                }
            }
        }

        return true
    }

    function backTracking() {
        for(let i = 0; i < board.length; i++) {
            for(let j = 0; j < board[0].length; j++) {
                if(board[i][j] !== '.') continue
                for(let val = 1; val <= 9; val++) {
                    if(isValid(i, j, `${val}`, board)) {
                        board[i][j] = `${val}`
                        if (backTracking()) {
                            return true
                        }

                        board[i][j] = `.`
                    }
                }
                return false
            }
        }
        return true
    }
    backTracking(board)
    return board
};

TypeScript

function isValid(col: number, row: number, val: string, board: string[][]): boolean {
    let n: number = board.length;
    for (let rowIndex = 0; rowIndex < n; rowIndex++) {
        if (board[rowIndex][col] === val) return false;
    }
    for (let colIndex = 0; colIndex < n; colIndex++) {
        if (board[row][colIndex] === val) return false;
    }
    const startX = Math.floor(col / 3) * 3;
    const startY = Math.floor(row / 3) * 3;
    for (let rowIndex = startY; rowIndex < startY + 3; rowIndex++) {
        for (let colIndex = startX; colIndex < startX + 3; colIndex++) {
            if (board[rowIndex][colIndex] === val) return false;
        }
    }
    return true;
}
function solveSudoku(board: string[][]): void {
    let n: number = 9;
    backTracking(n, board);
    function backTracking(n: number, board: string[][]): boolean {
        for (let row = 0; row < n; row++) {
            for (let col = 0; col < n; col++) {
                if (board[row][col] === '.') {
                    for (let i = 1; i <= n; i++) {
                        if (isValid(col, row, String(i), board)) {
                            board[row][col] = String(i);
                            if (backTracking(n, board) === true) return true;
                            board[row][col] = '.';
                        }
                    }
                    return false;
                }
            }
        }
        return true;
    }
};

Rust

impl Solution {
    fn is_valid(row: usize, col: usize, val: char, board: &mut Vec<Vec<char>>) -> bool{
        for i in 0..9 {
            if board[row][i] == val { return false; }
        }
        for j in 0..9 {
            if board[j][col] == val {
                return false;
            }
        }
        let  start_row = (row / 3) * 3;
        let  start_col = (col / 3) * 3;
        for i in start_row..(start_row + 3) {
            for j in start_col..(start_col + 3) {
                if board[i][j] == val { return false; }
            }
        }
        return true;
    }

    fn backtracking(board: &mut Vec<Vec<char>>) -> bool{
        for i in 0..board.len() {
            for j in 0..board[0].len() {
                if board[i][j] != '.' { continue; }
                for k in '1'..='9' {
                    if Solution::is_valid(i, j, k, board) {
                        board[i][j] = k;
                        if Solution::backtracking(board) { return true; }
                        board[i][j] = '.';
                    }
                }
                return false;
            }
        }
        return true;
    }

    pub fn solve_sudoku(board: &mut Vec<Vec<char>>) {
        Solution::backtracking(board);
    }
}

C

bool isValid(char** board, int row, int col, int k) {
    for (int i = 0; i < 9; i++) {
        if (board[i][col] == k) {
            return false;
        }
    }
    for (int j = 0; j < 9; j++) {
        if (board[row][j] == k) {
            return false;
        }
    }
    int startRow = (row / 3) * 3;
    int startCol = (col / 3) * 3;
    for (int i = startRow; i < startRow + 3; i++) {
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == k) {
                return false;
            }
        }
    }
    return true;
}

bool backtracking(char** board, int boardSize, int* boardColSize) {
    for (int i = 0; i < boardSize; i++) {
        for (int j = 0; j < *boardColSize; j++) {
            if (board[i][j] != '.') {
                continue;
            }
            for (int k = '1'; k <= '9'; k++) {
                if (isValid(board, i, j, k)) {
                    board[i][j] = k;
                    if (backtracking(board, boardSize, boardColSize)) {
                        return true;
                    }
                    board[i][j] = '.';
                }
            }
            return false;
        }
    }
    return true;
}

void solveSudoku(char** board, int boardSize, int* boardColSize) {
    bool res = backtracking(board, boardSize, boardColSize);
}

Swift

func solveSudoku(_ board: inout [[Character]]) {
    func isValid(row: Int, col: Int, val: Character) -> Bool {
        for i in 0 ..< 9 {
            if board[row][i] == val { return false }
        }
        for j in 0 ..< 9 {
            if board[j][col] == val { return false }
        }
        let startRow = row / 3 * 3
        let startCol = col / 3 * 3
        for i in startRow ..< startRow + 3 {
            for j in startCol ..< startCol + 3 {
                if board[i][j] == val { return false }
            }
        }
        return true
    }

    @discardableResult
    func backtracking() -> Bool {
        for i in 0 ..< board.count {
            for j in 0 ..< board[0].count {
                guard board[i][j] == "." else { continue } 
                for val in 1 ... 9 {
                    let charVal = Character("\(val)")
                    guard isValid(row: i, col: j, val: charVal) else { continue } 
                    board[i][j] = charVal 
                    if backtracking() { return true }
                    board[i][j] = "." 
                }
                return false 
            }
        }
        return true 
    }
    backtracking()
}

Scala

Detailed Writing:

object Solution {

  def solveSudoku(board: Array[Array[Char]]): Unit = {
    backtracking(board)
  }

  def backtracking(board: Array[Array[Char]]): Boolean = {
    for (i <- 0 until 9) {
      for (j <- 0 until 9) {
        if (board(i)(j) == '.') { // Must be number at . to place
          for (k <- '1' to '9') {
            if (isVaild(i, j, k, board)) {
              board(i)(j) = k
              if (backtracking(board)) return true
              board(i)(j) = '.'
            }
          }
          return false
        }
      }
    }
    true
  }

  def isVaild(x: Int, y: Int, value: Char, board: Array[Array[Char]]): Boolean = {
    for (i <- 0 until 9 ) {
      if (board(i)(y) == value) {
        return false
      }
    }
    for (j <- 0 until 9) {
      if (board(x)(j) == value) {
        return false
      }
    }
    var row = (x / 3) * 3
    var col = (y / 3) * 3
    for (i <- row until row + 3) {
      for (j <- col until col + 3) {
        if (board(i)(j) == value) {
          return false
        }
      }
    }
    true
  }
}

Scala Version Conforming to Scala Simplification Principles:

object Solution {

  def solveSudoku(board: Array[Array[Char]]): Unit = {
    backtracking(board)
  }

  def backtracking(board: Array[Array[Char]]): Boolean = {
    for (i <- 0 until 9; j <- 0 until 9 if board(i)(j) == '.') {
      for (k <- '1' to '9' if isVaild(i, j, k, board)) {
        board(i)(j) = k
        if (backtracking(board)) return true
        board(i)(j) = '.'
      }
      return false
    }
    true
  }

  def isVaild(x: Int, y: Int, value: Char, board: Array[Array[Char]]): Boolean = {
    for (i <- 0 until 9 if board(i)(y) == value) return false
    for (j <- 0 until 9 if board(x)(j) == value) return false
    var row = (x / 3) * 3
    var col = (y / 3) * 3
    for (i <- row until row + 3; j <- col until col + 3 if board(i)(j) == value) return false
    true
  }
}

C#

public class Solution
{
    public void SolveSudoku(char[][] board)
    {
        BackTracking(board);
    }
    public bool BackTracking(char[][] board)
    {
        for (int i = 0; i < board.Length; i++)
        {
            for (int j = 0; j < board[0].Length; j++)
            {
                if (board[i][j] != '.') continue;
                for (char k = '1'; k <= '9'; k++)
                {
                    if (IsValid(board, i, j, k))
                    {
                        board[i][j] = k;
                        if (BackTracking(board)) return true;
                        board[i][j] = '.';
                    }
                }
                return false;
            }

        }
        return true;
    }
    public bool IsValid(char[][] board, int row, int col, char val)
    {
        for (int i = 0; i < 9; i++)
        {
            if (board[i][col] == val) return false;
        }
        for (int i = 0; i < 9; i++)
        {
            if (board[row][i] == val) return false;
        }
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++)
        {
            for (int j = startCol; j < startCol + 3; j++)
            {
                if (board[i][j] == val) return false;
            }
        }
        return true;
    }
}