# Another Way of Implementing Deduplication in Backtracking
In the Weekly Summary! (Backtracking Series III) (opens new window), a participant raised a question about the entire tree's current level and the same node's current level, which also prompted me to rethink this issue. I found there was indeed a problem here, so I wrote a dedicated article to correct it. Thanks to all participants for their active discussions!
Let me explain this part again.
In Backtracking Algorithm: Subsets II (opens new window) and Backtracking Algorithm: Non-decreasing Subsequences (opens new window), deduplication is applied within the same level of the same parent node.
The Backtracking Algorithm: Subsets II (opens new window) can also use a set to deduplicate within the same parent's level, but why must the subset problem be sorted?
Let's use an unsorted set {2,1,2,2} as an example and draw a diagram, as shown below:
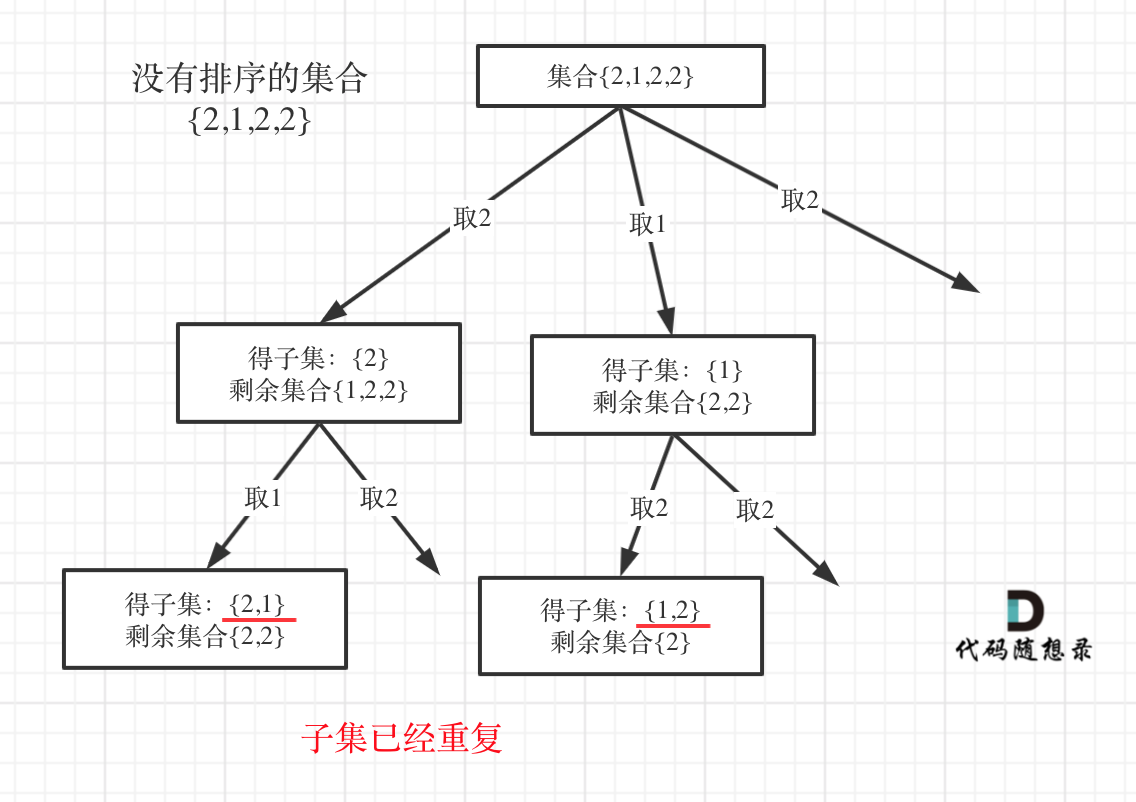
In the diagram, it is very clear that the subsets are duplicated.
Now, I will provide the code implementation that uses a set for deduplication within the same level for the Backtracking Algorithm: Subsets II (opens new window).
# 90. Subsets II
Version with a used array for deduplication: Backtracking Algorithm: Subsets II (opens new window)
Version with a set for deduplication is as follows:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
unordered_set<int> uset; // Define set for deduplication in the same node level
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) { // Skip if already found
continue;
}
uset.insert(nums[i]); // Update set with new element
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end()); // Sorting is required for deduplication
backtracking(nums, 0, used);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
To address the doubts of participants in the comments section, I will supplement with some common incorrect implementations.
# Incorrect Implementation One
Putting uset in the class member position and simulating backtracking by inserting once and erasing once.
For example:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
unordered_set<int> uset; // Define uset at class member position
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // Insert before recursion
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
uset.erase(nums[i]); // Erase during backtracking
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
In the tree structure, if the unordered_set<int> uset is placed at the class member level (equivalent to a global variable), it records the conditions of the branches, not just controlling the same level under one node.
As shown in the diagram:
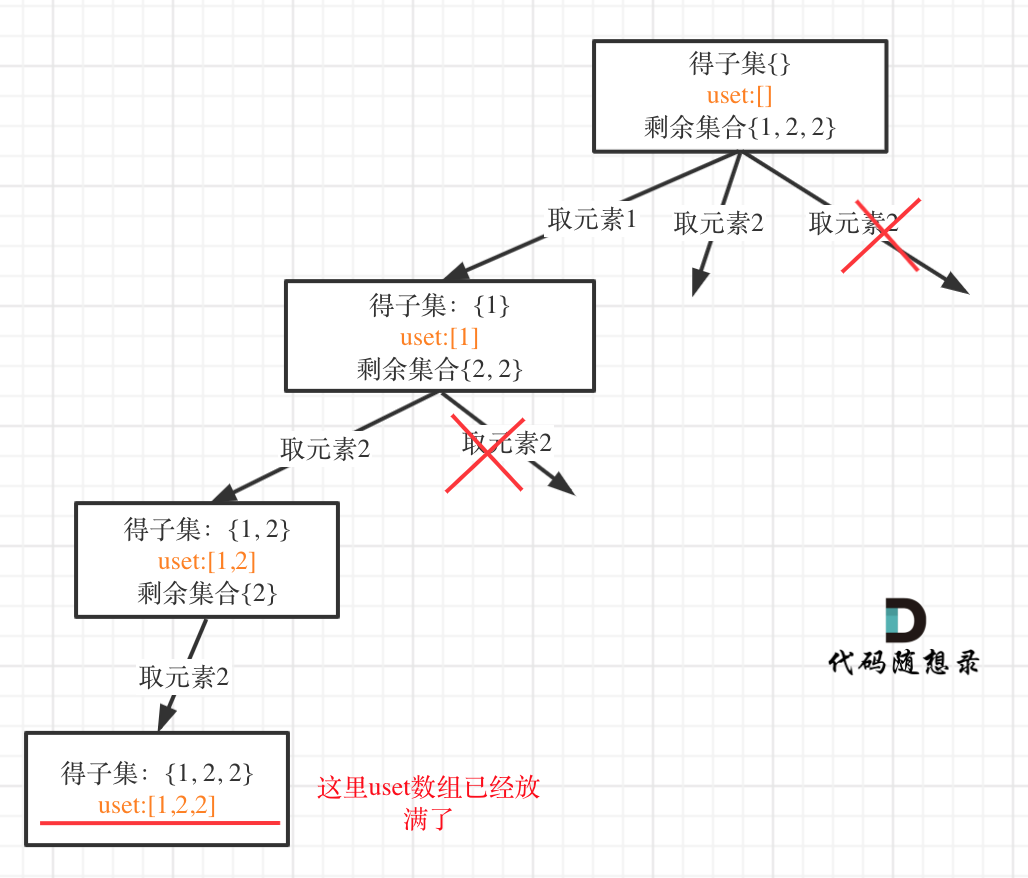
It is evident that when unordered_set<int> uset is placed at the class member level, it controls the whole tree, including the branches.
Therefore, this approach is not viable!
# Incorrect Implementation Two
Some users put unordered_set<int> uset; in the class member position and then clear uset each time they enter a single layer.
The code is as follows:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
unordered_set<int> uset; // Define uset at class member position
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
result.push_back(path);
uset.clear(); // Clear uset at each level
for (int i = startIndex; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
uset.insert(nums[i]); // Record element
path.push_back(nums[i]);
backtracking(nums, i + 1, used);
path.pop_back();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Since uset is already a global variable, the uset in the current level records one element, and after entering the next level, this uset (the same as the previous level) is cleared, meaning that uset between levels is the same, which leads to interference.
Therefore, this approach still doesn't work!
Combination and permutation problems can also use sets to deduplicate within the same node level, and I provide implementation code for both below.
# 40. Combination Sum II
Version with a used array for deduplication: Backtracking Algorithm: Combination Sum II (opens new window)
The version with a set for deduplication is as follows:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
return;
}
unordered_set<int> uset; // Control current node level to prevent duplicate elements
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
if (uset.find(candidates[i]) != uset.end()) {
continue;
}
uset.insert(candidates[i]); // Record element
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i + 1);
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
path.clear();
result.clear();
sort(candidates.begin(), candidates.end());
backtracking(candidates, target, 0, 0);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 47. Permutations II
Version with a used array for deduplication: Backtracking Algorithm: Permutations II (opens new window)
The version with a set for deduplication is as follows:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
unordered_set<int> uset; // Control current node level to prevent duplicate elements
for (int i = 0; i < nums.size(); i++) {
if (uset.find(nums[i]) != uset.end()) {
continue;
}
if (used[i] == false) {
uset.insert(nums[i]); // Record element
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // Sorting
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Performance Analysis of Two Implementations
It should be noted that: Using a set for deduplication is significantly less efficient than the version with a used array. This can be clearly observed by submitting on LeetCode.
As analyzed in Backtracking Algorithm: Non-decreasing Subsequences (opens new window), this is mainly because the frequent insertion into an unordered_set requires hash mapping (i.e., mapping the key with a hash function to a unique hash value), which is relatively time-consuming. Additionally, when inserting, its underlying symbol table also needs corresponding expansion, which is also time-consuming.
Using a used array incurs virtually no additional time complexity burden!
Using a set for deduplication not only increases the time complexity but also the space complexity, as analyzed in the Weekly Summary! (Backtracking Series III) (opens new window). The space complexity for combination, subset, and permutation problems is O(n), but it becomes O(n^2) when using a set for deduplication because each recursion level has a set collection, with the system stack space being n, and each space has a set collection.
Some may wonder that using a used array also occupies O(n) space?
The used array is a global variable, shared between levels, so the space complexity is O(n + n), ultimately remaining O(n).
# Summary
This article was initially intended to correct a point in Weekly Summary! (Backtracking Series III) (opens new window), but it turned into something extensive!
This point originated from a participant's question, leading me to think and summarize, ultimately writing this. So it's important to engage, right?
If you have any questions about the "Code Thought Record" articles, feel free to mention them in the comments when clocking in or ask in the discussion group.
This is indeed a mutual learning process; after a round of discussion, everyone will understand the problem more deeply. If I find issues in the articles, I will promptly correct them in the comments or the next article, ensuring not to lead you astray!
# Language Versions
# Java
47. Permutations II
class Solution {
private List<List<Integer>> res = new ArrayList<>();
private List<Integer> path = new ArrayList<>();
private boolean[] used = null;
public List<List<Integer>> permuteUnique(int[] nums) {
used = new boolean[nums.length];
Arrays.sort(nums);
backtracking(nums);
return res;
}
public void backtracking(int[] nums) {
if (path.size() == nums.length) {
res.add(new ArrayList<>(path));
return;
}
HashSet<Integer> hashSet = new HashSet<>();// Deduplicate within the level
for (int i = 0; i < nums.length; i++) {
if (hashSet.contains(nums[i]))
continue;
if (used[i] == true)// Deduplicate between branches
continue;
hashSet.add(nums[i]);// Record element
used[i] = true;
path.add(nums[i]);
backtracking(nums);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
90. Subsets II
class Solution {
List<List<Integer>> reslut = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
if(nums.length == 0){
reslut.add(path);
return reslut;
}
Arrays.sort(nums);
backtracking(nums,0);
return reslut;
}
public void backtracking(int[] nums,int startIndex){
reslut.add(new ArrayList<>(path));
if(startIndex >= nums.length)return;
HashSet<Integer> hashSet = new HashSet<>();
for(int i = startIndex; i < nums.length; i++){
if(hashSet.contains(nums[i])){
continue;
}
hashSet.add(nums[i]);
path.add(nums[i]);
backtracking(nums,i+1);
path.removeLast();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
40. Combination Sum II
class Solution {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort( candidates );
if( candidates[0] > target ) return result;
backtracking(candidates,target,0,0);
return result;
}
public void backtracking(int[] candidates,int target,int sum,int startIndex){
if( sum > target )return;
if( sum == target ){
result.add( new ArrayList<>(path) );
}
HashSet<Integer> hashSet = new HashSet<>();
for( int i = startIndex; i < candidates.length; i++){
if( hashSet.contains(candidates[i]) ){
continue;
}
hashSet.add(candidates[i]);
path.add(candidates[i]);
sum += candidates[i];
backtracking(candidates,target,sum,i+1);
path.removeLast();
sum -= candidates[i];
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Python
90. Subsets II
class Solution:
def subsetsWithDup(self, nums):
nums.sort() # Sorting required for deduplication
result = []
self.backtracking(nums, 0, [], result)
return result
def backtracking(self, nums, startIndex, path, result):
result.append(path[:])
used = set()
for i in range(startIndex, len(nums)):
if nums[i] in used:
continue
used.add(nums[i])
path.append(nums[i])
self.backtracking(nums, i + 1, path, result)
path.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
40. Combination Sum II
class Solution:
def combinationSum2(self, candidates, target):
candidates.sort()
result = []
self.backtracking(candidates, target, 0, 0, [], result)
return result
def backtracking(self, candidates, target, sum, startIndex, path, result):
if sum == target:
result.append(path[:])
return
used = set()
for i in range(startIndex, len(candidates)):
if sum + candidates[i] > target:
break
if candidates[i] in used:
continue
used.add(candidates[i])
sum += candidates[i]
path.append(candidates[i])
self.backtracking(candidates, target, sum, i + 1, path, result)
sum -= candidates[i]
path.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
47. Permutations II
class Solution:
def permuteUnique(self, nums):
nums.sort() # Sorting
result = []
self.backtracking(nums, [False] * len(nums), [], result)
return result
def backtracking(self, nums, used, path, result):
if len(path) == len(nums):
result.append(path[:])
return
used_set = set()
for i in range(len(nums)):
if nums[i] in used_set:
continue
if not used[i]:
used_set.add(nums[i])
used[i] = True
path.append(nums[i])
self.backtracking(nums, used, path, result)
path.pop()
used[i] = False
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# JavaScript
90. Subsets II
function subsetsWithDup(nums) {
nums.sort((a, b) => a - b);
const resArr = [];
backTraking(nums, 0, []);
return resArr;
function backTraking(nums, startIndex, route) {
resArr.push([...route]);
const helperSet = new Set();
for (let i = startIndex, length = nums.length; i < length; i++) {
if (helperSet.has(nums[i])) continue;
helperSet.add(nums[i]);
route.push(nums[i]);
backTraking(nums, i + 1, route);
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
40. Combination Sum II
function combinationSum2(candidates, target) {
candidates.sort((a, b) => a - b);
const resArr = [];
backTracking(candidates, target, 0, 0, []);
return resArr;
function backTracking( candidates, target, curSum, startIndex, route ) {
if (curSum > target) return;
if (curSum === target) {
resArr.push([...route]);
return;
}
const helperSet = new Set();
for (let i = startIndex, length = candidates.length; i < length; i++) {
let tempVal = candidates[i];
if (helperSet.has(tempVal)) continue;
helperSet.add(tempVal);
route.push(tempVal);
backTracking(candidates, target, curSum + tempVal, i + 1, route);
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
47. Permutations II
function permuteUnique(nums) {
const resArr = [];
const usedArr = [];
backTracking(nums, []);
return resArr;
function backTracking(nums, route) {
if (nums.length === route.length) {
resArr.push([...route]);
return;
}
const usedSet = new Set();
for (let i = 0, length = nums.length; i < length; i++) {
if (usedArr[i] === true || usedSet.has(nums[i])) continue;
usedSet.add(nums[i]);
route.push(nums[i]);
usedArr[i] = true;
backTracking(nums, route);
usedArr[i] = false;
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# TypeScript
90. Subsets II
function subsetsWithDup(nums: number[]): number[][] {
nums.sort((a, b) => a - b);
const resArr: number[][] = [];
backTraking(nums, 0, []);
return resArr;
function backTraking(nums: number[], startIndex: number, route: number[]): void {
resArr.push([...route]);
const helperSet: Set<number> = new Set();
for (let i = startIndex, length = nums.length; i < length; i++) {
if (helperSet.has(nums[i])) continue;
helperSet.add(nums[i]);
route.push(nums[i]);
backTraking(nums, i + 1, route);
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
40. Combination Sum II
function combinationSum2(candidates: number[], target: number): number[][] {
candidates.sort((a, b) => a - b);
const resArr: number[][] = [];
backTracking(candidates, target, 0, 0, []);
return resArr;
function backTracking(
candidates: number[], target: number,
curSum: number, startIndex: number, route: number[]
) {
if (curSum > target) return;
if (curSum === target) {
resArr.push([...route]);
return;
}
const helperSet: Set<number> = new Set();
for (let i = startIndex, length = candidates.length; i < length; i++) {
let tempVal: number = candidates[i];
if (helperSet.has(tempVal)) continue;
helperSet.add(tempVal);
route.push(tempVal);
backTracking(candidates, target, curSum + tempVal, i + 1, route);
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
47. Permutations II
function permuteUnique(nums: number[]): number[][] {
const resArr: number[][] = [];
const usedArr: boolean[] = [];
backTracking(nums, []);
return resArr;
function backTracking(nums: number[], route: number[]): void {
if (nums.length === route.length) {
resArr.push([...route]);
return;
}
const usedSet: Set<number> = new Set();
for (let i = 0, length = nums.length; i < length; i++) {
if (usedArr[i] === true || usedSet.has(nums[i])) continue;
usedSet.add(nums[i]);
route.push(nums[i]);
usedArr[i] = true;
backTracking(nums, route);
usedArr[i] = false;
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Rust
90. Subsets II:
use std::collections::HashSet;
impl Solution {
pub fn subsets_with_dup(mut nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut res = vec![];
let mut path = vec![];
nums.sort();
Self::backtracking(&nums, &mut path, &mut res, 0);
res
}
pub fn backtracking(
nums: &Vec<i32>,
path: &mut Vec<i32>,
res: &mut Vec<Vec<i32>>,
start_index: usize,
) {
res.push(path.clone());
let mut helper_set = HashSet::new();
for i in start_index..nums.len() {
if helper_set.contains(&nums[i]) {
continue;
}
helper_set.insert(nums[i]);
path.push(nums[i]);
Self::backtracking(nums, path, res, i + 1);
path.pop();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
40. Combination Sum II
use std::collections::HashSet;
impl Solution {
pub fn backtracking(
candidates: &Vec<i32>,
target: i32,
sum: i32,
path: &mut Vec<i32>,
res: &mut Vec<Vec<i32>>,
start_index: usize,
) {
if sum > target {
return;
}
if sum == target {
res.push(path.clone());
}
let mut helper_set = HashSet::new();
for i in start_index..candidates.len() {
if sum + candidates[i] <= target {
if helper_set.contains(&candidates[i]) {
continue;
}
helper_set.insert(candidates[i]);
path.push(candidates[i]);
Self::backtracking(candidates, target, sum + candidates[i], path, res, i + 1);
path.pop();
}
}
}
pub fn combination_sum2(mut candidates: Vec<i32>, target: i32) -> Vec<Vec<i32>> {
let mut res = vec![];
let mut path = vec![];
candidates.sort();
Self::backtracking(&candidates, target, 0, &mut path, &mut res, 0);
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
47. Permutations II
use std::collections::HashSet;
impl Solution {
pub fn permute_unique(mut nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut res = vec![];
let mut path = vec![];
let mut used = vec![false; nums.len()];
Self::backtracking(&mut res, &mut path, &nums, &mut used);
res
}
pub fn backtracking(
res: &mut Vec<Vec<i32>>,
path: &mut Vec<i32>,
nums: &Vec<i32>,
used: &mut Vec<bool>,
) {
if path.len() == nums.len() {
res.push(path.clone());
return;
}
let mut helper_set = HashSet::new();
for i in 0..nums.len() {
if used[i] || helper_set.contains(&nums[i]) {
continue;
}
helper_set.insert(nums[i]);
path.push(nums[i]);
used[i] = true;
Self::backtracking(res, path, nums, used);
used[i] = false;
path.pop();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
