77. Combination Optimization

Idea

In the Backtracking Algorithm: Finding Combination Issues! (opens new window), we addressed the problem of finding combinations of k numbers from n numbers using the backtracking search method.

The backtracking method described in the text can be optimized with pruning. In this article, we will continue to look at problem 77. Combinations.

Link: https://leetcode.com/problems/combinations/

Before reading this article, please first read Backtracking Algorithm: Finding Combination Issues! (opens new window).

Let's review the code for backtracking that was provided for [77. Combinations]:

class Solution {
private:
    vector<vector<int>> result; // A collection that stores sets that meet criteria
    vector<int> path; // Used to store sets that meet criteria
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i); // Process node
            backtracking(n, k, i + 1); // Recursion
            path.pop_back(); // Backtrack, revoke node processing
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear(); // Can be omitted
        path.clear();   // Can be omitted
        backtracking(n, k, 1);
        return result;
    }
};

Pruning Optimization

We've discussed that even though the backtracking method is essentially a brute force search, it can sometimes be slightly optimized using pruning.

Consider the following code during traversal:

for (int i = startIndex; i <= n; i++) {
    path.push_back(i);
    backtracking(n, k, i + 1);
    path.pop_back();
}

The range of this traversal can be optimized. How can it be optimized?

Let's use an example. If n = 4 and k = 4, then during the first layer of the for loop, starting traversal from element 2 has no meaning. In the second layer of the for loop, starting traversal from element 3 has no meaning either.

This might sound abstract, so let's include an illustrative diagram:

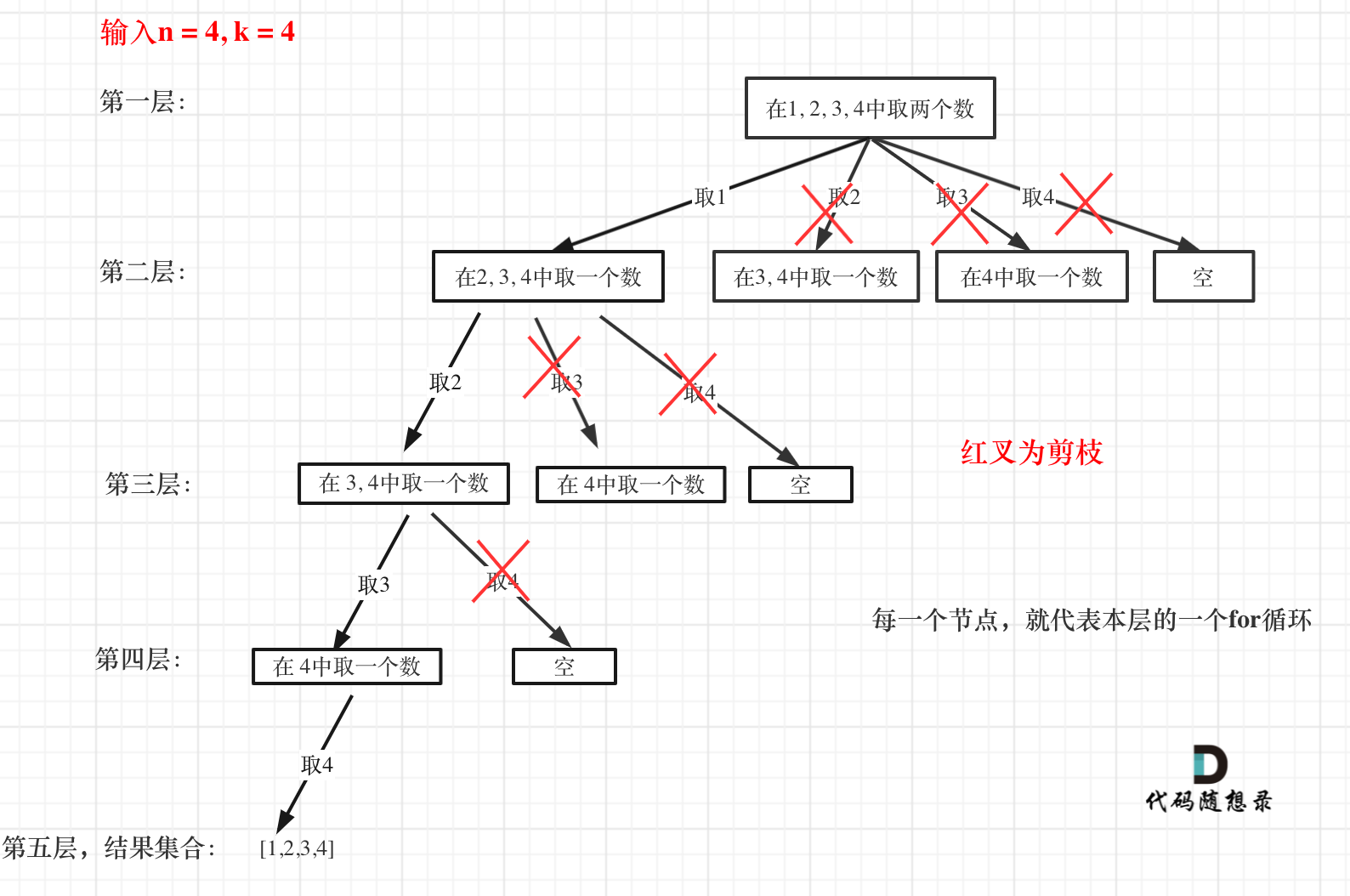
In this diagram, each node (represented as a rectangle) signifies a for loop at the current level. If each layer of the for loop starts from the second element, it's meaningless and amounts to invalid traversal.

Thus, the place where pruning can happen is in the starting position chosen by the for loop in each level of recursion.

If the elements remaining after the starting position in the for loop are already less than the number of elements required, there's no need to search further.

Note that the code mentions i as the starting point of selection for the for loop.

for (int i = startIndex; i <= n; i++) {

Here is the optimization process:

1. Number of chosen elements: path.size();

2. Required number of elements: k - path.size();

3. Remaining elements in the list (n-i) >= Required elements (k - path.size());

4. At most, start from position: i <= n - (k - path.size()) + 1 in the set n.

Why the +1? Because the starting position is included, making this a left-closed set.

For example, if n = 4, k = 3, and already chosen elements are 0 (path.size is 0), then n - (k - 0) + 1 equates to 4 - (3 - 0) + 1 = 2.

Starting from 2, the search is reasonable and could be a combination [2, 3, 4].

If this isn't clear, you might find it beneficial to create an example of your own to determine whether you need +1.

Thus, the optimized for loop is:

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i is the starting position for this search

The complete optimized code is as follows:

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // Optimization happens here
            path.push_back(i); // Process node
            backtracking(n, k, i + 1);
            path.pop_back(); // Backtrack, revoke node processing
        }
    }
public:

    vector<vector<int>> combine(int n, int k) {
        backtracking(n, k, 1);
        return result;
    }
};

• Time Complexity: O(n * 2^n)
• Space Complexity: O(n)

Summary

In this post, we optimized the pruning of backtracking code for the combination problem. Without diagrams, this optimization is actually hard to understand and explain clearly.

So I've once again abstracted the entire backtracking process into a tree-like structure, making it visually clear which parts of the process are being pruned.

That's it! If you've learned something, please share this with others to let more fans know where to find this content!

Other Language Versions

Java

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combine(int n, int k) {
        combineHelper(n, k, 1);
        return result;
    }

    /**
     * Each time choosing elements from the set, the range of selectable elements shrinks as the selection progresses, and adjusting this range relies on startIndex.
     * @param startIndex Used to record where the set starts traversing in this layer of recursion (the set is {1,...,n}).
     */
    private void combineHelper(int n, int k, int startIndex){
        // Base case
        if (path.size() == k){
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
            path.add(i);
            combineHelper(n, k, i + 1);
            path.removeLast();
        }
    }
}

Python

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        result = []  # Store result set
        self.backtracking(n, k, 1, [], result)
        return result
    def backtracking(self, n, k, startIndex, path, result):
        if len(path) == k:
            result.append(path[:])
            return
        for i in range(startIndex, n - (k - len(path)) + 2):  # Optimized
            path.append(i)  # Process node
            self.backtracking(n, k, i + 1, path, result)
            path.pop()  # Backtrack, revoke node processing

Go

var (
    path []int
    res  [][]int
)

func combine(n int, k int) [][]int {
    path, res = make([]int, 0, k), make([][]int, 0)
    dfs(n, k, 1)
    return res
}

func dfs(n int, k int, start int) {
    if len(path) == k {  
        tmp := make([]int, k)
        copy(tmp, path)
        res = append(res, tmp)
        return 
    }
    for i := start; i <= n - (k-len(path)) + 1; i++ {  
        path = append(path, i)
        dfs(n, k, i+1)
        path = path[:len(path)-1]
    }
}

JavaScript

var combine = function(n, k) {
    const res = [], path = [];
    backtracking(n, k, 1);
    return res;
    function backtracking (n, k, i){
        const len = path.length;
        if(len === k) {
            res.push(Array.from(path));
            return;
        }
        for(let a = i; a <= n + len - k + 1; a++) {
            path.push(a);
            backtracking(n, k, a + 1);
            path.pop();
        }
    }
};

TypeScript

function combine(n: number, k: number): number[][] {
    let resArr: number[][] = [];
    function backTracking(n: number, k: number, startIndex: number, tempArr: number[]): void {
        if (tempArr.length === k) {
            resArr.push(tempArr.slice());
            return;
        }
        for (let i = startIndex; i <= n - k + 1 + tempArr.length; i++) {
            tempArr.push(i);
            backTracking(n, k, i + 1, tempArr);
            tempArr.pop();
        }
    }
    backTracking(n, k, 1, []);
    return resArr;
};

Rust

impl Solution {
    fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, n: i32, k: i32, start_index: i32) {
        let len= path.len() as i32;
        if len == k{
            result.push(path.to_vec());
            return;
        }
	// Pruning here
        for i in start_index..= n - (k - len) + 1 {
            path.push(i);
            Self::backtracking(result, path, n, k, i+1);
            path.pop();
        }
    }
    pub fn combine(n: i32, k: i32) -> Vec<Vec<i32>> {
        let mut result = vec![];
        let mut path = vec![];
        Self::backtracking(&mut result, &mut path, n, k, 1);
        result
    }
}

C

int* path;
int pathTop;
int** ans;
int ansTop;

void backtracking(int n, int k,int startIndex) {
    // When the number of elements in the path is k, store the path array in the ans 2D array
    if(pathTop == k) {
        // The path array is dynamically allocated. If we directly store its address in the 2D array, the values will change as we backtrack
        // Thus, we create a new array to store the values in path
        int* temp = (int*)malloc(sizeof(int) * k);
        int i;
        for(i = 0; i < k; i++) {
            temp[i] = path[i];
        }
        ans[ansTop++] = temp;
        return ;
    }

    int j;
    for(j = startIndex; j <= n- (k - pathTop) + 1;j++) {
        // Add current node to path array
        path[pathTop++] = j;
        // Recurse further
        backtracking(n, k, j + 1);
        // Backtrack, pop top node from array
        pathTop--;
    }
}

int** combine(int n, int k, int* returnSize, int** returnColumnSizes){
    // Path array: store qualifying results
    path = (int*)malloc(sizeof(int) * k);
    // Ans 2D array: store the collection of result arrays that meet the criteria (big enough to avoid extreme cases)
    ans = (int**)malloc(sizeof(int*) * 10000);
    pathTop = ansTop = 0;

    // Backtracking algorithm
    backtracking(n, k, 1);
    // Final return size is the size of ans array
    *returnSize = ansTop;
    // ReturnColumnSizes array stores lengths of 1D arrays corresponding to indexes in ans (all k)
    *returnColumnSizes = (int*)malloc(sizeof(int) *(*returnSize));
    int i;
    for(i = 0; i < *returnSize; i++) {
        (*returnColumnSizes)[i] = k;
    }
    // Return the ans 2D array
    return ans;
}

Swift

func combine(_ n: Int, _ k: Int) -> [[Int]] {
    var path = [Int]()
    var result = [[Int]]()
    func backtracking(start: Int) {
        // Termination condition and collect results
        if path.count == k {
            result.append(path)
            return
        }

        // Single layer logic
        // let end = n
        // Pruning optimization
        let end = n - (k - path.count) + 1
        guard start <= end else { return }
        for i in start ... end {
            path.append(i) // Process node
            backtracking(start: i + 1) // Recurse
            path.removeLast() // Backtrack
        }
    }

    backtracking(start: 1)
    return result
}

Scala

object Solution {
  import scala.collection.mutable // Import
  def combine(n: Int, k: Int): List[List[Int]] = {
    var result = mutable.ListBuffer[List[Int]]() // Store result set
    var path = mutable.ListBuffer[Int]() // Store sets that meet criteria

    def backtracking(n: Int, k: Int, startIndex: Int): Unit = {
      if (path.size == k) {
        // If path's size == k, meets requirements, add to result set, and return
        result.append(path.toList)
        return
      }
      // Pruning optimization
      for (i <- startIndex to (n - (k - path.size) + 1)) { 
        path.append(i) // Add number first
        backtracking(n, k, i + 1) // Next backtrack step
        path = path.take(path.size - 1) // Backtrack complete, delete just added number
      }
    }

    backtracking(n, k, 1) // Execute backtracking
    result.toList // Ultimately return result in List form, `return` keyword can be omitted
  }
}