90. Subsets II

LeetCode Problem Link (opens new window)

Given an integer array nums that may contain duplicates, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

Example:

• Input: [1,2,2]
• Output: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

Approach

You should solve 0078.Subsets (opens new window) before attempting this problem.

The difference between this problem and 0078.Subsets (opens new window) is that this one allows duplicates in the input array, and we must ensure that the subsets are unique.

For removing duplicates in backtracking problems, we have already elaborated on the technique thoroughly in 0040.Combination Sum II (opens new window), and this problem follows the same pattern.

To reveal a bit more, the technique for removing duplicates is crucial for permutation problems we cover later, so understanding the concept of “unique levels” and “unique branches” is highly significant.

Using the example [1, 2, 2], the solution is as depicted in the diagram: (Note that to ensure uniqueness, sorting the array is necessary)

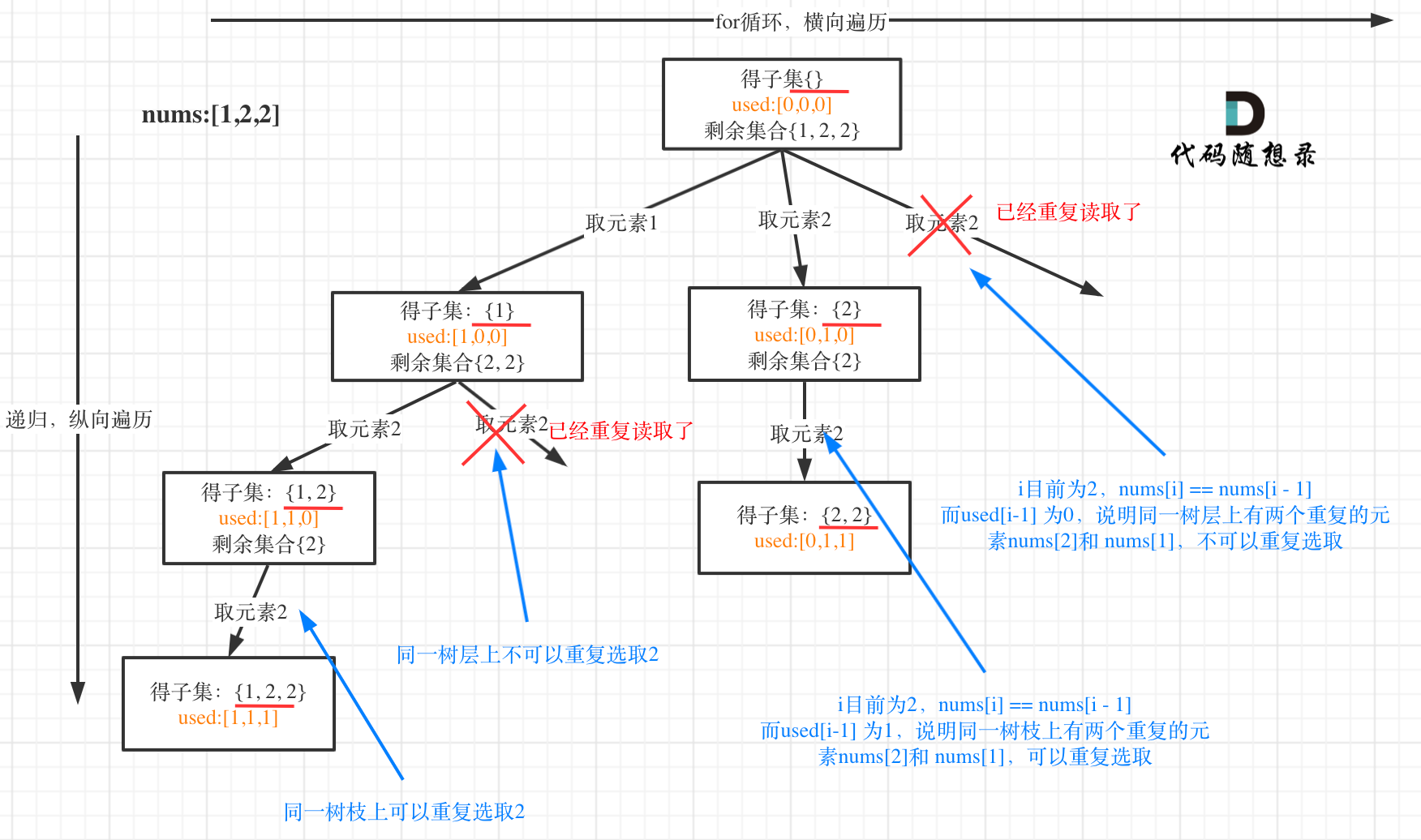
From the diagram, you can see that you should skip repeated occurrences of 2 on the same level. On the same branch, however, it is necessary to include the repeated element 2, as the entire set of elements on a branch uniquely determines a subset!

This problem is essentially an extension of the Backtracking Algorithm: Subset Problem! (opens new window) with the added requirement to remove duplicates, a technique already discussed in Backtracking Algorithm: Combination Sum III (opens new window), so I'll directly provide the code:

The C++ code is as follows:

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used) {
        result.push_back(path);
        for (int i = startIndex; i < nums.size(); i++) {
            // used[i - 1] == true, indicates that candidates[i - 1] was used on the same branch
            // used[i - 1] == false, indicates that candidates[i - 1] was used on the same level
            // We skip elements used on the same level
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            path.push_back(nums[i]);
            used[i] = true;
            backtracking(nums, i + 1, used);
            used[i] = false;
            path.pop_back();
        }
    }

public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end()); // Sort needed for deduplication
        backtracking(nums, 0, used);
        return result;
    }
};

• Time Complexity: O(n * 2^n)
• Space Complexity: O(n)

Version that uses a set for deduplication:

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex) {
        result.push_back(path);
        unordered_set<int> uset;
        for (int i = startIndex; i < nums.size(); i++) {
            if (uset.find(nums[i]) != uset.end()) {
                continue;
            }
            uset.insert(nums[i]);
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }

public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        result.clear();
        path.clear();
        sort(nums.begin(), nums.end()); // Sort needed for deduplication
        backtracking(nums, 0);
        return result;
    }
};

Additional Notes

It is also possible to solve this problem without using a used array because during recursion, the next startIndex is i + 1 instead of 0.

If it were a full permutation, where we need to traverse from 0 every time, we would need used to skip over elements that have already been stacked.

The code is as follows:

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& nums, int startIndex) {
        result.push_back(path);
        for (int i = startIndex; i < nums.size(); i++) {
            // We skip elements already used on the same level
            if (i > startIndex && nums[i] == nums[i - 1]) { // Note i > startIndex here
                continue;
            }
            path.push_back(nums[i]);
            backtracking(nums, i + 1);
            path.pop_back();
        }
    }

public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        result.clear();
        path.clear();
        sort(nums.begin(), nums.end()); // Sort needed for deduplication
        backtracking(nums, 0);
        return result;
    }
};

Conclusion

The knowledge points for this problem have been covered in earlier problems. If you have mastered the subset and deduplication problems covered before, you should be able to quickly solve this one.

Other Language Versions

Java

Using used array

class Solution {
   List<List<Integer>> result = new ArrayList<>();// Collection of results meeting the conditions
   LinkedList<Integer> path = new LinkedList<>();// Used to store results that meet the conditions
   boolean[] used;
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        if (nums.length == 0){
            result.add(path);
            return result;
        }
        Arrays.sort(nums);
        used = new boolean[nums.length];
        subsetsWithDupHelper(nums, 0);
        return result;
    }
    
    private void subsetsWithDupHelper(int[] nums, int startIndex){
        result.add(new ArrayList<>(path));
        if (startIndex >= nums.length){
            return;
        }
        for (int i = startIndex; i < nums.length; i++){
            if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
                continue;
            }
            path.add(nums[i]);
            used[i] = true;
            subsetsWithDupHelper(nums, i + 1);
            path.removeLast();
            used[i] = false;
        }
    }
}

Without used array

class Solution {

  List<List<Integer>> res = new ArrayList<>();
  LinkedList<Integer> path = new LinkedList<>();
  
  public List<List<Integer>> subsetsWithDup( int[] nums ) {
    Arrays.sort( nums );
    subsetsWithDupHelper( nums, 0 );
    return res;
  }


  private void subsetsWithDupHelper( int[] nums, int start ) {
    res.add( new ArrayList<>( path ) );

    for ( int i = start; i < nums.length; i++ ) {
        // Skip elements already used on the same level
      if ( i > start && nums[i - 1] == nums[i] ) {
        continue;
      }
      path.add( nums[i] );
      subsetsWithDupHelper( nums, i + 1 );
      path.removeLast();
    }
  }

}

Python3

Backtracking using used array for deduplication

class Solution:
    def subsetsWithDup(self, nums):
        result = []
        path = []
        used = [False] * len(nums)
        nums.sort()  # Sorting needed for deduplication
        self.backtracking(nums, 0, used, path, result)
        return result

    def backtracking(self, nums, startIndex, used, path, result):
        result.append(path[:])  # Collect the subset
        for i in range(startIndex, len(nums)):
            # used[i - 1] == True means the element used on the same branch
            # used[i - 1] == False means the element used on the same level
            # We skip elements used on the same level
            if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
                continue
            path.append(nums[i])
            used[i] = True
            self.backtracking(nums, i + 1, used, path, result)
            used[i] = False
            path.pop()

Backtracking using a set for deduplication

class Solution:
    def subsetsWithDup(self, nums):
        result = []
        path = []
        nums.sort()  # Sorting needed for deduplication
        self.backtracking(nums, 0, path, result)
        return result

    def backtracking(self, nums, startIndex, path, result):
        result.append(path[:])  # Collect the subset
        uset = set()
        for i in range(startIndex, len(nums)):
            if nums[i] in uset:
                continue
            uset.add(nums[i])
            path.append(nums[i])
            self.backtracking(nums, i + 1, path, result)
            path.pop()

Backtracking using startIndex increment for deduplication

class Solution:
    def subsetsWithDup(self, nums):
        result = []
        path = []
        nums.sort()  # Sorting needed for deduplication
        self.backtracking(nums, 0, path, result)
        return result

    def backtracking(self, nums, startIndex, path, result):
        result.append(path[:])  # Collect the subset
        for i in range(startIndex, len(nums)):
            # We skip elements already used on the same level
            if i > startIndex and nums[i] == nums[i - 1]:
                continue
            path.append(nums[i])
            self.backtracking(nums, i + 1, path, result)
            path.pop()

Go

Using used array

var (
    result [][]int
    path []int
)

func subsetsWithDup(nums []int) [][]int {
    result = make([][]int, 0)
    path = make([]int, 0)
    used := make([]bool, len(nums))
    sort.Ints(nums) // Sorting needed for deduplication
    backtracing(nums, 0, used)
    return result
}

func backtracing(nums []int, startIndex int, used []bool) {
    tmp := make([]int, len(path))
    copy(tmp, path)
    result = append(result, tmp)
    for i := startIndex; i < len(nums); i++ {
        // used[i - 1] == true means the element was used on the same branch
        // used[i - 1] == false means the element was used on the same level
        // We skip elements used on the same level
        if i > 0 && nums[i] == nums[i-1] && used[i-1] == false {
            continue
        }
        path = append(path, nums[i])
        used[i] = true
        backtracing(nums, i + 1, used)
        path = path[:len(path)-1]
        used[i] = false
    }
}

Without used array

var (
    path   []int
    res  [][]int
)
func subsetsWithDup(nums []int) [][]int {
    path, res = make([]int, 0, len(nums)), make([][]int, 0)
    sort.Ints(nums)
    dfs(nums, 0)
    return res
}

func dfs(nums []int, start int) {
    tmp := make([]int, len(path))
    copy(tmp, path)
    res = append(res, tmp)

    for i := start; i < len(nums); i++ {
        if i != start && nums[i] == nums[i-1] {
            continue
        }
        path = append(path, nums[i])
        dfs(nums, i+1)
        path = path[:len(path)-1]
    }
}

JavaScript

var subsetsWithDup = function(nums) {
    let result = []
    let path = []
    let sortNums = nums.sort((a, b) => {
        return a - b
    })
    function backtracing(startIndex, sortNums) {
        result.push([...path])
        if(startIndex > nums.length - 1) {
            return
        }
        for(let i = startIndex; i < nums.length; i++) {
            if(i > startIndex && nums[i] === nums[i - 1]) {
                continue
            }
            path.push(nums[i])
            backtracing(i + 1, sortNums)
            path.pop()
        }
    }
    backtracing(0, sortNums)
    return result
};

TypeScript

function subsetsWithDup(nums: number[]): number[][] {
    nums.sort((a, b) => a - b);
    const resArr: number[][] = [];
    backTraking(nums, 0, []);
    return resArr;
    function backTraking(nums: number[], startIndex: number, route: number[]): void {
        resArr.push([...route]);
        let length: number = nums.length;
        if (startIndex === length) return;
        for (let i = startIndex; i < length; i++) {
            if (i > startIndex && nums[i] === nums[i - 1]) continue;
            route.push(nums[i]);
            backTraking(nums, i + 1, route);
            route.pop();
        }
    }
};

Version with set deduplication:

// Version with set deduplication
function subsetsWithDup(nums: number[]): number[][] {
    const result: number[][] = [];
    const path: number[] = [];
    // Sorting is required before deduplication
    nums.sort((a, b) => a - b);
    function backTracking(startIndex: number) {
        // Collect results
        result.push([...path])
        // Even if not returning here, because the recursion increments startIndex, when it is big enough it will not recurse further.
        if (startIndex === nums.length) {
            return
        }
        // Define a set for each tree level
        const set: Set<number> = new Set()
        for (let i = startIndex; i < nums.length; i++) {
            // Deduplicate
            if (set.has(nums[i])) {
                continue
            }
            set.add(nums[i])
            path.push(nums[i])
            backTracking(i + 1)
            // Backtrack
            path.pop()
        }
    }
    backTracking(0)
    return result
};

Rust

impl Solution {
    fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, start_index: usize, used: &mut Vec<bool>) {
        result.push(path.clone());
        let len = nums.len();
        // if start_index >= len { return; }
        for i in start_index..len {
            if i > 0 && nums[i] == nums[i - 1] && !used[i - 1] { continue; }
            path.push(nums[i]);
            used[i] = true;
            Self::backtracking(result, path, nums, i + 1, used);
            used[i] = false;
            path.pop();
        }
    }

    pub fn subsets_with_dup(mut nums: Vec<i32>) -> Vec<Vec<i32>> {
        let mut result: Vec<Vec<i32>> = Vec::new();
        let mut path: Vec<i32> = Vec::new();
        let mut used = vec![false; nums.len()];
        nums.sort();
        Self::backtracking(&mut result, &mut path, &nums, 0, &mut used);
        result
    }
}

Version with set deduplication

use std::collections::HashSet;
impl Solution {
    pub fn subsets_with_dup(mut nums: Vec<i32>) -> Vec<Vec<i32>> {
        let mut res = HashSet::new();
        let mut path = vec![];
        nums.sort();
        Self::backtracking(&nums, &mut path, &mut res, 0);
        res.into_iter().collect()
    }

    pub fn backtracking(
        nums: &Vec<i32>,
        path: &mut Vec<i32>,
        res: &mut HashSet<Vec<i32>>,
        start_index: usize,
    ) {
        res.insert(path.clone());
        for i in start_index..nums.len() {
            path.push(nums[i]);
            Self::backtracking(nums, path, res, i + 1);
            path.pop();
        }
    }
}

C

int* path;
int pathTop;
int** ans;
int ansTop;
// Responsible for storing the length of each array in the 2D array
int* lengths;
// Quick sort compare function
int cmp(const void* a, const void* b) {
    return *((int*)a) - *((int*)b);
}

// Copy function, copies the current path to ans. Also records the path length
void copy() {
    int* tempPath = (int*)malloc(sizeof(int) * pathTop);
    int i;
    for(i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    ans = (int**)realloc(ans, sizeof(int*) * (ansTop + 1));
    lengths[ansTop] = pathTop;
    ans[ansTop++] = tempPath;
}

void backTracking(int* nums, int numsSize, int startIndex, int* used) {
    // First copy the current path
    copy();
    // Return if startIndex is beyond the last element's position
    if(startIndex >= numsSize)
        return ;
    
    int i;
    for(i = startIndex; i < numsSize; i++) {
        // Skip repeated elements used on the same level
        if(i > 0 && nums[i] ==  nums[i-1] && used[i-1] == false) 
            continue;
        path[pathTop++] = nums[i];
        used[i] = true;
        backTracking(nums, numsSize, i + 1, used);
        used[i] = false;
        pathTop--;
    }
}

int** subsetsWithDup(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    // Declare auxiliary variables
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(0);
    lengths = (int*)malloc(sizeof(int) * 1500);
    int* used = (int*)malloc(sizeof(int) * numsSize);
    pathTop = ansTop = 0;

    // Sorting is needed before deduplication
    qsort(nums, numsSize, sizeof(int), cmp);
    backTracking(nums, numsSize, 0, used);

    // Set the return sizes of the 1D and 2D arrays
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = lengths[i];
    }
    return ans;
}

Swift

func subsetsWithDup(_ nums: [Int]) -> [[Int]] {
    let nums = nums.sorted()
    var result = [[Int]]()
    var path = [Int]()
    func backtracking(startIndex: Int) {
        // Directly collect results
        result.append(path)

        let end = nums.count
        guard startIndex < end else { return } // Termination condition
        for i in startIndex ..< end {
            if i > startIndex, nums[i] == nums[i - 1] { continue } // Skip duplicate elements
            path.append(nums[i]) // Process: collect elements
            backtracking(startIndex: i + 1) // Elements are not revisited
            path.removeLast() // Backtrack
        }
    }
    backtracking(startIndex: 0)
    return result
}

Scala

Without used array:

object Solution {
  import scala.collection.mutable
  def subsetsWithDup(nums: Array[Int]): List[List[Int]] = {
    var result = mutable.ListBuffer[List[Int]]()
    var path = mutable.ListBuffer[Int]()
    var num = nums.sorted // Sort

    def backtracking(startIndex: Int): Unit = {
      result.append(path.toList)
      if (startIndex >= num.size){
        return
      }
      for (i <- startIndex until num.size) {
        // Skip duplicate elements on the same level
        if (!(i > startIndex && num(i) == num(i - 1))) {
          path.append(num(i))
          backtracking(i + 1)
          path.remove(path.size - 1)
        }
      }
    }

    backtracking(0)
    result.toList
  }
}

Using Set for deduplication:

object Solution {
  import scala.collection.mutable
  def subsetsWithDup(nums: Array[Int]): List[List[Int]] = {
    var result = mutable.Set[List[Int]]()
    var num = nums.sorted
    def backtracking(path: mutable.ListBuffer[Int], startIndex: Int): Unit = {
      if (startIndex == num.length) {
        result.add(path.toList)
        return
      }
      path.append(num(startIndex))
      backtracking(path, startIndex + 1)  // Choose
      path.remove(path.size - 1)
      backtracking(path, startIndex + 1)  // Do not choose
    }

    backtracking(mutable.ListBuffer[Int](), 0)

    result.toList
  }
}

C#

public class Solution
{
    public IList<IList<int>> res = new List<IList<int>>();
    public IList<int> path = new List<int>();
    public IList<IList<int>> SubsetsWithDup(int[] nums)
    {
        Array.Sort(nums);
        BackTracking(nums, 0);
        return res;
    }
    public void BackTracking(int[] nums, int start)
    {
        res.Add(new List<int>(path));
        for (int i = start; i < nums.Length; i++)
        {
            if (i > start && nums[i] == nums[i - 1]) continue;
            path.Add(nums[i]);
            BackTracking(nums, i + 1);
            path.RemoveAt(path.Count - 1);
        }
    }
}