keetcoder

# 39. Combination Sum

LeetCode Problem Link (opens new window)

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

  • All numbers (including target) are positive integers.
  • The solution set must not contain duplicate combinations.

Example 1:

  • Input: candidates = [2,3,6,7], target = 7,
  • Output: [ [7], [2,2,3] ]

Example 2:

  • Input: candidates = [2,3,5], target = 8,
  • Output: [ [2,2,2,2], [2,3,3], [3,5] ]

# Approach

The problem states that numbers in candidates can be chosen repeatedly. This implies situations where 0 might appear, but given that all numbers are positive integers, this is not a concern.

This problem bears similarities to 0077.Combinations (opens new window) and 0216.Combination Sum III (opens new window) in that it involves generating combinations. However, unlike those problems, this one has no limit on the number of times a number can be selected, albeit with an overall sum constraint.

Visualizing the search process as a tree structure, consider the following diagram:

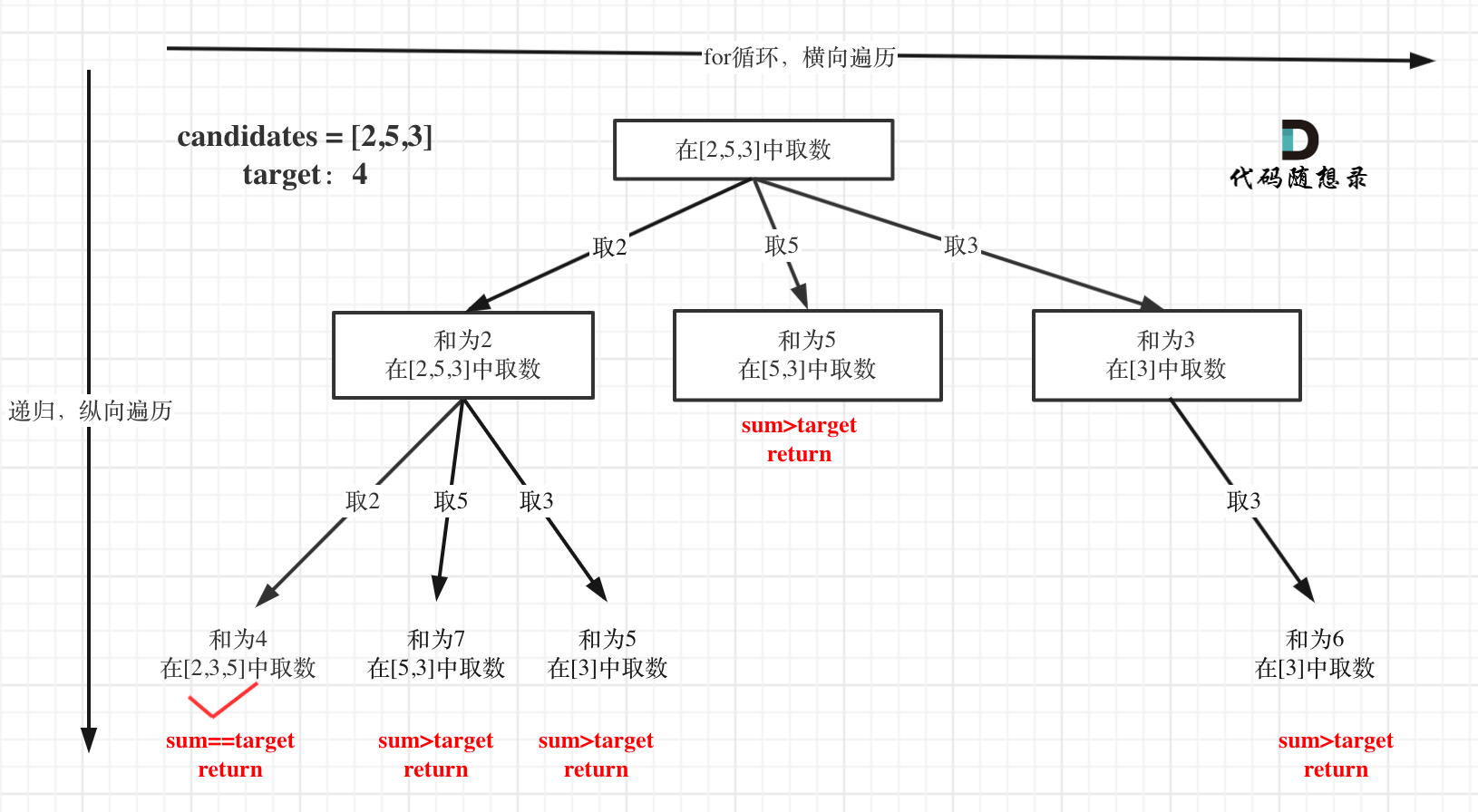39. Combination Sum Notice that leaf nodes return once the sum exceeds or equals the target. Here, there is no limit on the depth of recursion, only on the sum. Unlike problems 0077.Combinations (opens new window) and 0216.Combination Sum III (opens new window), where a fixed number of elements is chosen, this problem has varying depths based on the cumulative sum.

# Backtracking Steps

  • Recursive Function Parameters

Define two global variables: a 2D array result to store results, and an array path for conditions that fit. Additional parameters include the candidates array and the target value. An integer sum is used to track the sum of path. Optionally, target could handle sum checks directly, but using sum clarifies logic.

Crucially, startIndex manages the starting point of the for loop. It indicates continuous selection, proving essential in problems like 0077.Combinations (opens new window) and 0216.Combination Sum III (opens new window).

Here's the function definition:

vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex)
1
2
3
  • Termination Conditions

From the tree diagram:

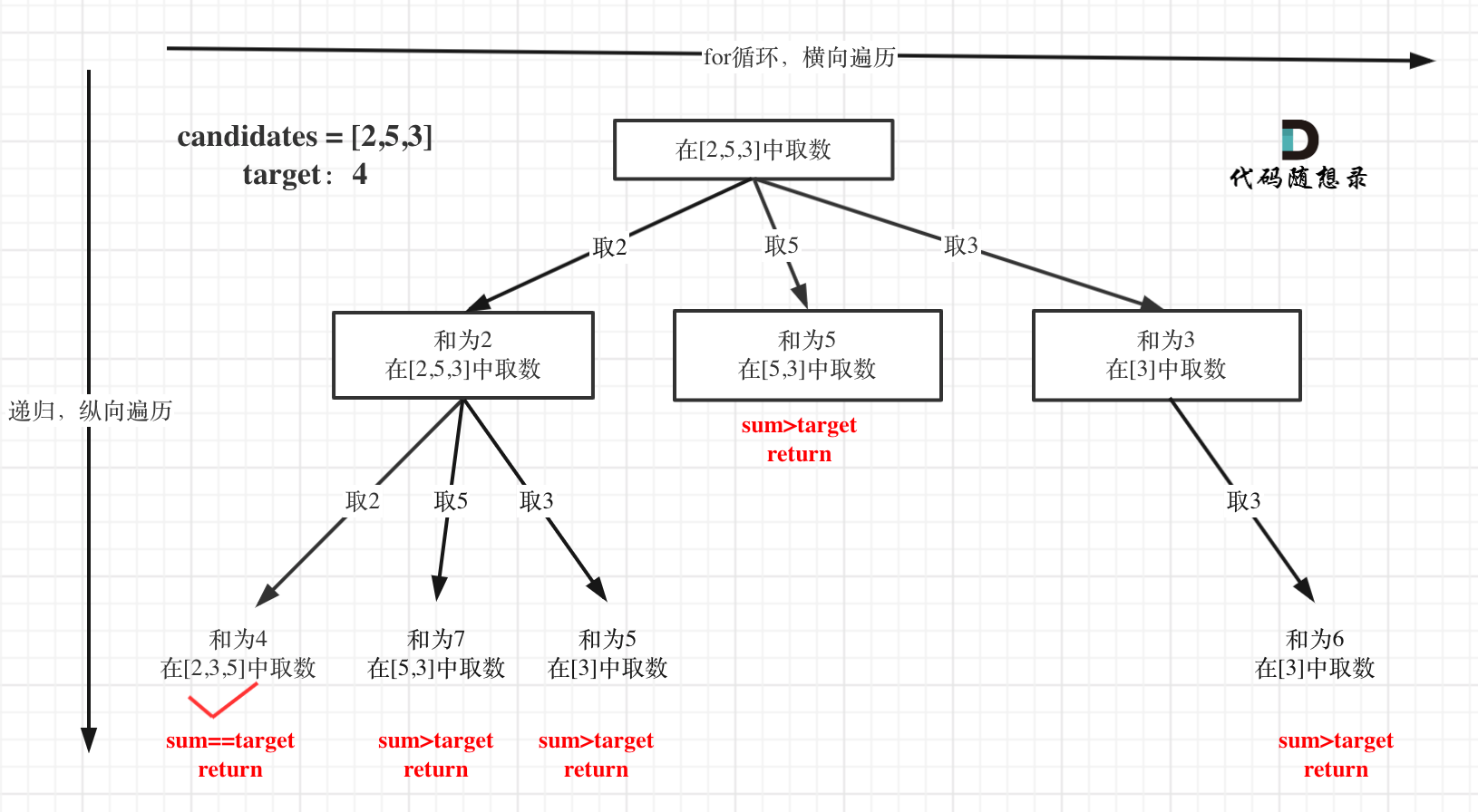
39. Combination Sum

Termination occurs only when sum exceeds or equals target.

If sum equals target, collect this path in result:

if (sum > target) {
    return;
}
if (sum == target) {
    result.push_back(path);
    return;
}
1
2
3
4
5
6
7
  • Single-layer Search Logic

Start the loop from startIndex and search through candidates. Here, elements can be selected repeatedly:

for (int i = startIndex; i < candidates.size(); i++) {
    sum += candidates[i];
    path.push_back(candidates[i]);
    backtracking(candidates, target, sum, i); // Key point: do not use i+1, allowing re-selection of current number
    sum -= candidates[i];   // Backtrack
    path.pop_back();        // Backtrack
}
1
2
3
4
5
6
7

Following the template from Backtracking Algorithm Fundamentals (opens new window), the complete C++ code is:

// Version 1
class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum > target) {
            return;
        }
        if (sum == target) {
            result.push_back(path);
            return;
        }

        for (int i = startIndex; i < candidates.size(); i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i); // Allow repeat selection
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        result.clear();
        path.clear();
        backtracking(candidates, target, 0, 0);
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# Pruning Optimization

In the tree structure and above Version 1 code, for scenarios where sum already exceeds target, the recursion still goes one level deeper. It would be better to avoid this if the next level sum exceeds target.

By sorting, prune the loop if cumulative sum already exceeds target. Illustrated visually:

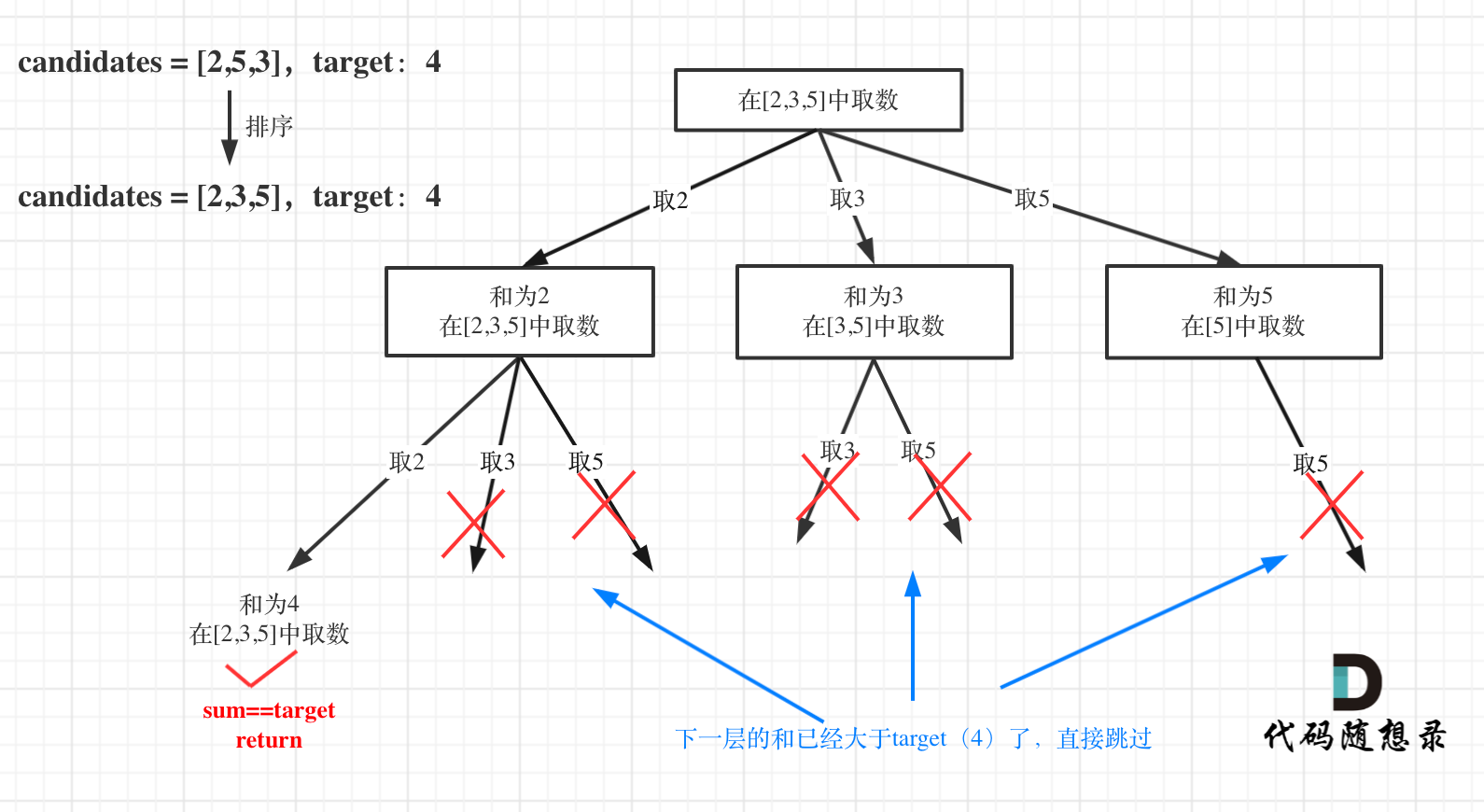
39. Combination Sum

Pruning:

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
1

Overall code, noting annotations:

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            result.push_back(path);
            return;
        }

        // If sum + candidates[i] > target stop iterating
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        result.clear();
        path.clear();
        sort(candidates.begin(), candidates.end()); // Necessary to sort
        backtracking(candidates, target, 0, 0);
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
  • Time complexity: O(n * 2^n), this is an upper bound due to pruning reducing practical complexity
  • Space complexity: O(target)

# Summary

This problem contrasts 0077.Combinations (opens new window) and 0216.Combination Sum III (opens new window) mainly on two fronts:

  • No quantity limit on combinations
  • Elements can be selected repeatedly

We detailed when to use startIndex, in comparison with scenarios like 0017.Letter Combinations of a Phone Number (opens new window). Final pruning optimizations, common in summing problems, were introduced.

The goal is to deeply understand problems by comparing and highlighting differences, which facilitates better solution strategies.

# Other Language Versions

# Java

// With pruning optimization
class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates); // Sort first
        backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
        return res;
    }

    public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = idx; i < candidates.length; i++) {
            if (sum + candidates[i] > target) break;
            path.add(candidates[i]);
            backtracking(res, path, candidates, target, sum + candidates[i], i);
            path.remove(path.size() - 1);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Python

Backtracking (Version 1)

class Solution:

    def backtracking(self, candidates, target, total, startIndex, path, result):
        if total > target:
            return
        if total == target:
            result.append(path[:])
            return

        for i in range(startIndex, len(candidates)):
            total += candidates[i]
            path.append(candidates[i])
            self.backtracking(candidates, target, total, i, path, result)  # Repeated selection allowed
            total -= candidates[i]
            path.pop()

    def combinationSum(self, candidates, target):
        result = []
        self.backtracking(candidates, target, 0, 0, [], result)
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Backtracking with pruning (Version 1)

class Solution:

    def backtracking(self, candidates, target, total, startIndex, path, result):
        if total == target:
            result.append(path[:])
            return

        for i in range(startIndex, len(candidates)):
            if total + candidates[i] > target:
                break
            total += candidates[i]
            path.append(candidates[i])
            self.backtracking(candidates, target, total, i, path, result)
            total -= candidates[i]
            path.pop()

    def combinationSum(self, candidates, target):
        result = []
        candidates.sort()  # Necessary to sort
        self.backtracking(candidates, target, 0, 0, [], result)
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Backtracking (Version 2)

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        result =[]
        self.backtracking(candidates, target, 0, [], result)
        return result
    def backtracking(self, candidates, target, startIndex, path, result):
        if target == 0:
            result.append(path[:])
            return
        if target < 0:
            return
        for i in range(startIndex, len(candidates)):
            path.append(candidates[i])
            self.backtracking(candidates, target - candidates[i], i, path, result)
            path.pop()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Backtracking with pruning (Version 2)

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        result =[]
        candidates.sort()
        self.backtracking(candidates, target, 0, [], result)
        return result
    def backtracking(self, candidates, target, startIndex, path, result):
        if target == 0:
            result.append(path[:])
            return

        for i in range(startIndex, len(candidates)):
            if target - candidates[i]  < 0:
                break
            path.append(candidates[i])
            self.backtracking(candidates, target - candidates[i], i, path, result)
            path.pop()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# Go

Mainly focuses on recursive descent

var (
    res [][]int
    path  []int
)
func combinationSum(candidates []int, target int) [][]int {
    res, path = make([][]int, 0), make([]int, 0, len(candidates))
    sort.Ints(candidates)   // Sort for pruning
    dfs(candidates, 0, target)
    return res
}

func dfs(candidates []int, start int, target int) {
    if target == 0 {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }
    for i := start; i < len(candidates); i++ {
        if candidates[i] > target {
            break
        }
        path = append(path, candidates[i])
        dfs(candidates, i, target - candidates[i])
        path = path[:len(path) - 1]
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# JavaScript

var combinationSum = function(candidates, target) {
    const res = [], path = [];
    candidates.sort((a,b)=>a-b); // Sort
    backtracking(0, 0);
    return res;
    function backtracking(j, sum) {
        if (sum === target) {
            res.push(Array.from(path));
            return;
        }
        for(let i = j; i < candidates.length; i++ ) {
            const n = candidates[i];
            if(n > target - sum) break;
            path.push(n);
            sum += n;
            backtracking(i, sum);
            path.pop();
            sum -= n;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# TypeScript

function combinationSum(candidates: number[], target: number): number[][] {
    const resArr: number[][] = [];
    function backTracking(
        candidates: number[], target: number,
        startIndex: number, route: number[], curSum: number
    ): void {
        if (curSum > target) return;
        if (curSum === target) {
            resArr.push(route.slice());
            return
        }
        for (let i = startIndex, length = candidates.length; i < length; i++) {
            let tempVal: number = candidates[i];
            route.push(tempVal);
            backTracking(candidates, target, i, route, curSum + tempVal);
            route.pop();
        }
    }
    backTracking(candidates, target, 0, [], 0);
    return resArr;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# Rust

impl Solution {
    pub fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, candidates: &Vec<i32>, target: i32, mut sum: i32, start_index: usize) {
        if sum == target {
            result.push(path.to_vec());
            return;
        }
        for i in start_index..candidates.len() {
            if sum + candidates[i] <= target {
                sum += candidates[i];
                path.push(candidates[i]);
                Self::backtracking(result, path, candidates, target, sum, i);
                sum -= candidates[i];
                path.pop();
            }
        }
    }

    pub fn combination_sum(candidates: Vec<i32>, target: i32) -> Vec<Vec<i32>> {
        let mut result: Vec<Vec<i32>> = Vec::new();
        let mut path: Vec<i32> = Vec::new();
        Self::backtracking(&mut result, &mut path, &candidates, target, 0, 0);
        result
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# C

int* path;
int pathTop;
int** ans;
int ansTop;
// Store lengths of each path where sum equals target
int* length;

void backTracking(int target, int index, int* candidates, int candidatesSize, int sum) {
    if(sum >= target) {
        if(sum == target) {
            int* tempPath = (int*)malloc(sizeof(int) * pathTop);
            int j;
            for(j = 0; j < pathTop; j++) {
                tempPath[j] = path[j];
            }
            ans[ansTop] = tempPath;
            length[ansTop++] = pathTop;
        }
        return;
    }

    int i;
    for(i = index; i < candidatesSize; i++) {
        sum += candidates[i];
        path[pathTop++] = candidates[i];
        backTracking(target, i, candidates, candidatesSize, sum);
        sum -= candidates[i];
        pathTop--;
    }
}

int** combinationSum(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
    path = (int*)malloc(sizeof(int) * 50);
    ans = (int**)malloc(sizeof(int*) * 200);
    length = (int*)malloc(sizeof(int) * 200);
    ansTop = pathTop = 0;
    backTracking(target, 0, candidates, candidatesSize, 0);

    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = length[i];
    }
    return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# Swift

func combinationSum(_ candidates: [Int], _ target: Int) -> [[Int]] {
    var result = [[Int]]()
    var path = [Int]()
    func backtracking(sum: Int, startIndex: Int) {
        if sum == target {
            result.append(path)
            return
        }

        let end = candidates.count
        guard startIndex < end else { return }
        for i in startIndex..<end {
            let sum = sum + candidates[i]
            if sum > target { continue }

            path.append(candidates[i])
            backtracking(sum: sum, startIndex: i)
            path.removeLast()
        }
    }
    backtracking(sum: 0, startIndex: 0)
    return result
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Scala

object Solution {
  import scala.collection.mutable
  def combinationSum(candidates: Array[Int], target: Int): List[List[Int]] = {
    var result = mutable.ListBuffer[List[Int]]()
    var path = mutable.ListBuffer[Int]()

    def backtracking(sum: Int, index: Int): Unit = {
      if (sum == target) {
        result.append(path.toList)
        return
      }

      for (i <- index until candidates.size if sum + candidates(i) <= target) {
        path.append(candidates(i))
        backtracking(sum + candidates(i), i)
        path = path.take(path.size - 1)
      }
    }

    backtracking(0, 0)
    result.toList
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# C#

public class Solution
{
    public IList<IList<int>> res = new List<IList<int>>();
    public IList<int> path = new List<int>();
    public IList<IList<int>> CombinationSum(int[] candidates, int target)
    {
        BackTracking(candidates, target, 0, 0);
        return res;
    }
    public void BackTracking(int[] candidates, int target, int start, int sum)
    {
        if (sum > target) return;
        if (sum == target)
        {
            res.Add(new List<int>(path));
            return;
        }
        for (int i = start; i < candidates.Length; i++)
        {
            sum += candidates[i];
            path.Add(candidates[i]);
            BackTracking(candidates, target, i, sum);
            sum -= candidates[i];
            path.RemoveAt(path.Count - 1);
        }
    }
}

// With pruning optimization
public class Solution
{
    public IList<IList<int>> res = new List<IList<int>>();
    public IList<int> path = new List<int>();
    public IList<IList<int>> CombinationSum(int[] candidates, int target)
    {
        Array.Sort(candidates);
        BackTracking(candidates, target, 0, 0);
        return res;
    }
    public void BackTracking(int[] candidates, int target, int start, int sum)
    {
        if (sum > target) return;
        if (sum == target)
        {
            res.Add(new List<int>(path));
            return;
        }
        for (int i = start; i < candidates.Length && sum + candidates[i] <= target; i++)
        {
            sum += candidates[i];
            path.Add(candidates[i]);
            BackTracking(candidates, target, i, sum);
            sum -= candidates[i];
            path.RemoveAt(path.Count - 1);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
Last updated:: 9/4/2025, 3:19:38 PM

← 7. Combination Sum II →

Copyright © 2025 keetcoder