# 47. Permutations II
LeetCode Problem Link (opens new window)
Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.
Example 1:
- Input: nums = [1,1,2]
- Output: [ [1,1,2], [1,2,1], [2,1,1] ]
Example 2:
- Input: nums = [1,2,3]
- Output: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
Constraints:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
# Strategy
This problem differs from 0046.Permutations (opens new window) in that the sequence may contain duplicate numbers and requires returning all unique permutations.
This problem involves deduplication.
In problems like 0040.Combination Sum II (opens new window) and 0090.Subsets II (opens new window), we have discussed how to handle deduplication in detail for both combination and subset problems.
Permutations are essentially handled similarly.
It is crucial to sort the elements for deduplication so that we can easily check adjacent elements to determine if they have been used repetitively.
Using the sorted example of [1,1,2] as a demonstration, the deduplication process can be visualized as:
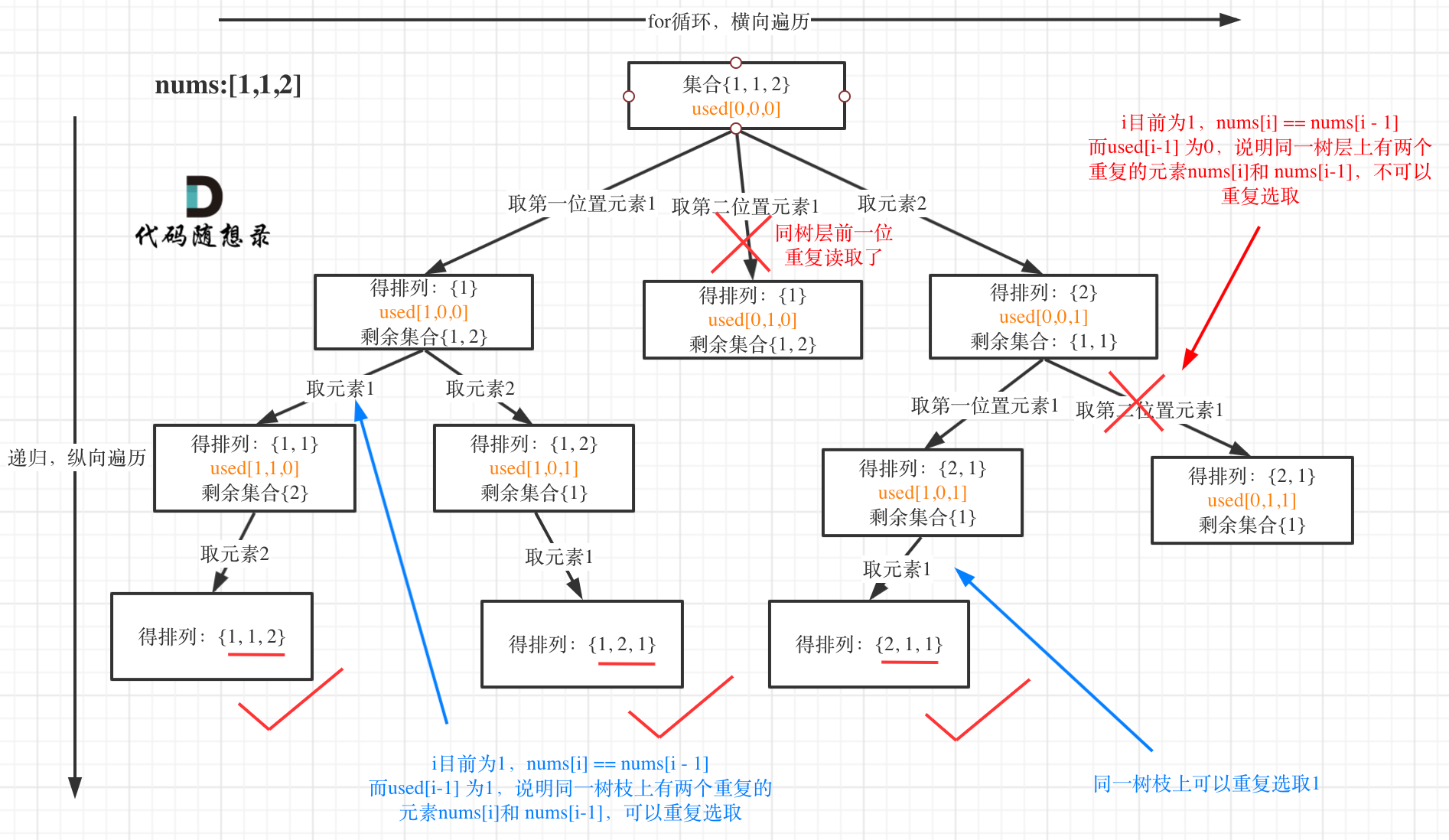
In the graph, for the same level in the tree, if the previous value (i.e., nums[i-1]) has been used, it should be skipped to avoid duplicates.
Typically, combinations and permutation problems involve collecting results at the leaf nodes of a tree structure, whereas subset problems involve collecting results at all nodes.
In 0046.Permutations (opens new window), we have detailed the approach to solve permutation problems, and in 0040.Combination Sum II (opens new window) and 0090.Subsets II (opens new window), the deduplication methods have been explained. Let’s jump to the code:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// If a valid permutation is found
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
// If the element is the same as the previous one and has been used in the same tree level, skip it
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
if (used[i] == false) {
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
}
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // Sort the array
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
// Time Complexity: In the worst case where all elements are unique, the complexity is O(n! * n). There are n! permutations. For each answer, we need O(n) to copy it to the result array.
// Space Complexity: O(n), as the depth of the recursion tree is determined by the number of elements.
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
- Time Complexity: O(n! * n)
- Space Complexity: O(n)
# Expansion
The key deduplication code is:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
2
3
It is also correct to replace it with used[i - 1] == true. The deduplication code would be:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
continue;
}
2
3
Why is this possible? As mentioned before, deduplication across the same tree level uses used[i - 1] == false, while deduplication across the same tree branch uses used[i - 1] == true.
For permutation problems, both tree level deduplication and tree branch deduplication are feasible, although tree level deduplication is more efficient!
Does this sound abstract? Let me illustrate with an example using the input: [1,1,1].
Tree level deduplication (used[i - 1] == false) results in the following tree structure:
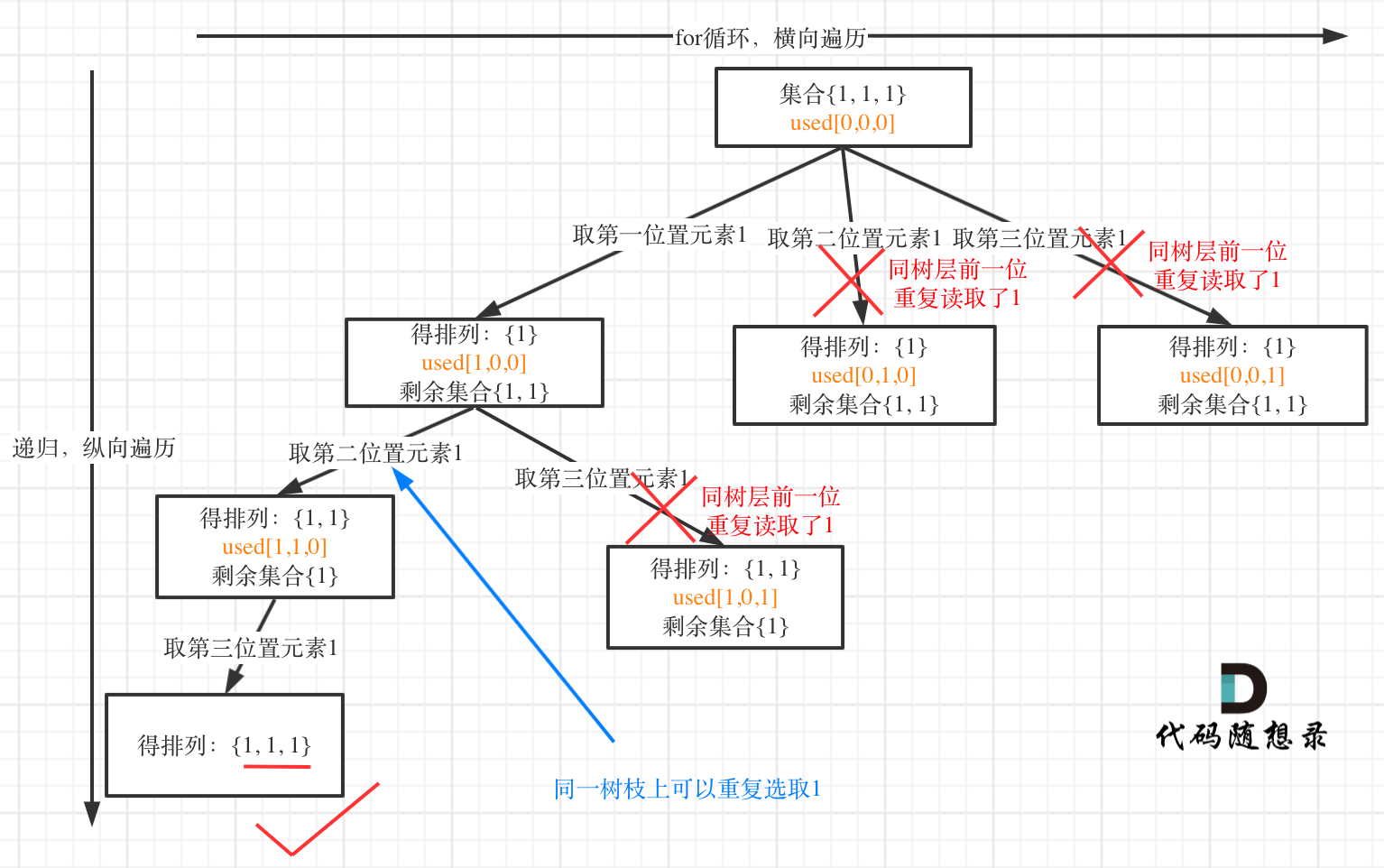
Tree branch deduplication (used[i - 1] == true) results in the following tree structure:

It’s clear that deduplication at the tree level is more efficient, as it avoids redundant searches, unlike tree branch deduplication.
# Conclusion
This problem applies previous deduplication techniques. Interestingly, deduplication conditions such as:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
2
3
and:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
continue;
}
2
3
both work, but understanding why can be puzzling for many. By illustrating the tree structures for input [1,1,1], we can clearly identify why two approaches work and which is more efficient!
You might ask, if both used[i - 1] == false and used[i - 1] == true work, why add this condition at all?
Why not write it simply:
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
2
3
This doesn’t work. The used[i - 1] condition ensures either continuous true or false states, which matters, instead of switching randomly. Hence, this condition is needed.
Does it make sense now?
# Code in Other Languages
# Java
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
boolean[] used = new boolean[nums.length];
Arrays.fill(used, false);
Arrays.sort(nums);
backTrack(nums, used);
return result;
}
private void backTrack(int[] nums, boolean[] used) {
if (path.size() == nums.length) {
result.add(new ArrayList<>(path));
return;
}
for (int i = 0; i < nums.length; i++) {
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
continue;
}
if (used[i] == false) {
used[i] = true;
path.add(nums[i]);
backTrack(nums, used);
path.remove(path.size() - 1);
used[i] = false;
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Python
class Solution:
def permuteUnique(self, nums):
nums.sort() # Sort the list
result = []
self.backtracking(nums, [], [False] * len(nums), result)
return result
def backtracking(self, nums, path, used, result):
if len(path) == len(nums):
result.append(path[:])
return
for i in range(len(nums)):
if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
continue
used[i] = True
path.append(nums[i])
self.backtracking(nums, path, used, result)
path.pop()
used[i] = False
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Go
var (
res [][]int
path []int
st []bool // Abbreviation for state
)
func permuteUnique(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
st = make([]bool, len(nums))
sort.Ints(nums)
dfs(nums, 0)
return res
}
func dfs(nums []int, cur int) {
if cur == len(nums) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
}
for i := 0; i < len(nums); i++ {
if i != 0 && nums[i] == nums[i-1] && !st[i-1] { // Deduplication, using st to differentiate levels
continue
}
if !st[i] {
path = append(path, nums[i])
st[i] = true
dfs(nums, cur + 1)
st[i] = false
path = path[:len(path)-1]
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# JavaScript
var permuteUnique = function (nums) {
nums.sort((a, b) => a - b);
let result = [];
let path = [];
function backtracing(used) {
if (path.length === nums.length) {
result.push([...path]);
return;
}
for (let i = 0; i < nums.length; i++) {
if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {
continue;
}
if (!used[i]) {
used[i] = true;
path.push(nums[i]);
backtracing(used);
path.pop();
used[i] = false;
}
}
}
backtracing([]);
return result;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# TypeScript
function permuteUnique(nums: number[]): number[][] {
nums.sort((a, b) => a - b);
const resArr: number[][] = [];
const usedArr: boolean[] = new Array(nums.length).fill(false);
backTracking(nums, []);
return resArr;
function backTracking(nums: number[], route: number[]): void {
if (route.length === nums.length) {
resArr.push([...route]);
return;
}
for (let i = 0, length = nums.length; i < length; i++) {
if (i > 0 && nums[i] === nums[i - 1] && usedArr[i - 1] === false) continue;
if (usedArr[i] === false) {
route.push(nums[i]);
usedArr[i] = true;
backTracking(nums, route);
usedArr[i] = false;
route.pop();
}
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Swift
func permuteUnique(_ nums: [Int]) -> [[Int]] {
let nums = nums.sorted() // Sorts the array
var result = [[Int]]()
var path = [Int]()
var used = [Bool](repeating: false, count: nums.count)
func backtracking() {
if path.count == nums.count {
result.append(path)
return
}
for i in 0 ..< nums.count {
if i > 0, nums[i] == nums[i - 1], !used[i - 1] { continue }
if used[i] { continue }
used[i] = true
path.append(nums[i])
backtracking()
// Backtracking
path.removeLast()
used[i] = false
}
}
backtracking()
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Rust
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, used: &mut Vec<bool>) {
let len = nums.len();
if path.len() == len {
result.push(path.clone());
return;
}
for i in 0..len {
if i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false { continue; }
if used[i] == false {
used[i] = true;
path.push(nums[i]);
Self::backtracking(result, path, nums, used);
path.pop();
used[i] = false;
}
}
}
pub fn permute_unique(nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut path: Vec<i32> = Vec::new();
let mut used = vec![false; nums.len()];
let mut nums= nums;
nums.sort();
Self::backtracking(&mut result, &mut path, &nums, &mut used);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# C
// Temporary array
int *path;
// Return array
int **ans;
int *used;
int pathTop, ansTop;
// Copy path to ans
void copyPath() {
int *tempPath = (int*)malloc(sizeof(int) * pathTop);
int i;
for(i = 0; i < pathTop; ++i) {
tempPath[i] = path[i];
}
ans[ansTop++] = tempPath;
}
void backTracking(int* used, int *nums, int numsSize) {
if(pathTop == numsSize)
copyPath();
int i;
for(i = 0; i < numsSize; i++) {
if(used[i] || (i != 0 && nums[i] == nums[i-1] && used[i-1] == 0))
continue;
used[i] = 1;
path[pathTop++] = nums[i];
backTracking(used, nums, numsSize);
used[i] = 0;
--pathTop;
}
}
int cmp(void* elem1, void* elem2) {
return *((int*)elem1) - *((int*)elem2);
}
int** permuteUnique(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
qsort(nums, numsSize, sizeof(int), cmp);
pathTop = ansTop = 0;
path = (int*)malloc(sizeof(int) * numsSize);
ans = (int**)malloc(sizeof(int*) * 1000);
used = (int*)malloc(sizeof(int) * numsSize);
int i;
for(i = 0; i < numsSize; i++) {
used[i] = 0;
}
backTracking(used, nums, numsSize);
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int z;
for(z = 0; z < ansTop; z++) {
(*returnColumnSizes)[z] = numsSize;
}
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# Scala
object Solution {
import scala.collection.mutable
def permuteUnique(nums: Array[Int]): List[List[Int]] = {
var result = mutable.ListBuffer[List[Int]]()
var path = mutable.ListBuffer[Int]()
var num = nums.sorted // Firstly, sort the data
def backtracking(used: Array[Boolean]): Unit = {
if (path.size == num.size) {
result.append(path.toList)
return
}
for (i <- num.indices if used(i) == false) {
if (i == 0 || (i > 0 && num(i) != num(i - 1)) || used(i-1) == false) {
used(i) = true
path.append(num(i))
backtracking(used)
path.remove(path.size - 1)
used(i) = false
}
}
}
backtracking(new Array[Boolean](nums.length))
result.toList
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# C#
public class Solution
{
public List<IList<int>> res = new List<IList<int>>();
public List<int> path = new List<int>();
public IList<IList<int>> PermuteUnique(int[] nums)
{
Array.Sort(nums);
BackTracking(nums, new bool[nums.Length]);
return res;
}
public void BackTracking(int[] nums, bool[] used)
{
if (nums.Length == path.Count)
{
res.Add(new List<int>(path));
return;
}
for (int i = 0; i < nums.Length; i++)
{
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;
if (used[i]) continue;
path.Add(nums[i]);
used[i] = true;
BackTracking(nums, used);
path.RemoveAt(path.Count - 1);
used[i] = false;
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
