# Hash Table Basics
# Hash Table
First, what is a hash table? A hash table (known as Hash table in English; in some algorithm books in China, it’s also translated as scatter table) is a data structure that accesses by using the value of the key directly.
A hash table is a data structure that provides direct access based on the value of the key.
This official explanation might be a bit confusing. In simpler terms, an array is essentially a hash table.
In a hash table, the key is the index of the array, which allows direct access to elements using the index, as shown in the figure below:
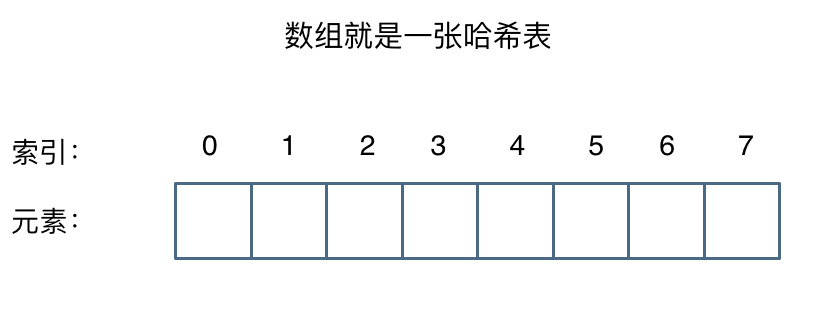
So, what problem does a hash table solve? Typically, hash tables are used to quickly determine whether an element appears in a collection.
For example, if you want to check whether a name is in a school.
Using enumeration, the time complexity is O(n), but if you use a hash table, you can achieve this in O(1) time.
All we need to do is store all the student names in the hash table, and then use the index to check if a student is in the school.
Mapping student names onto a hash table involves a hash function.
# Hash Function
A hash function maps the student's name directly to the index on a hash table, allowing us to quickly determine if the student is in the school by checking the index.
As illustrated in the figure below, hashCode converts names into numeric values. Generally, hashCode uses a specific encoding scheme to convert other data formats into unique numbers, thus mapping student names to index numbers on the hash table.
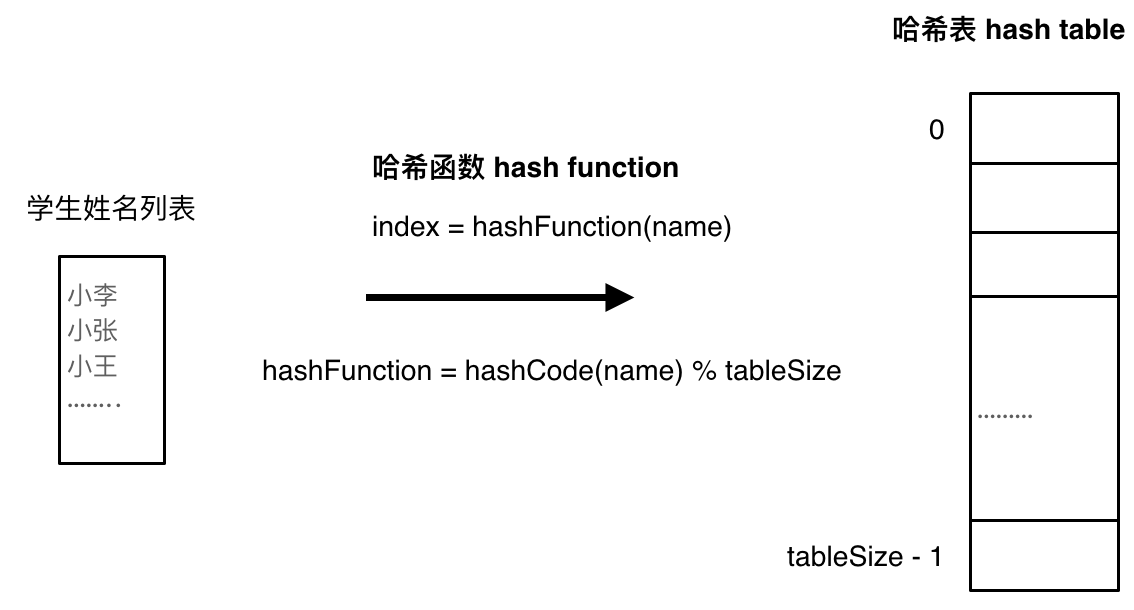
What if the value obtained by hashCode exceeds the size of the hash table?
To ensure that the mapped index values fall on the hash table, we'll perform a modulus operation on the value. This ensures that the student name can always be mapped to the hash table.
This brings us to another problem: the hash table is essentially an array.
What if the number of students exceeds the size of the hash table? In this case, even the most evenly distributed hash function can't prevent several student names from mapping to the same index.
Hash collision comes into play at this point.
# Hash Collision
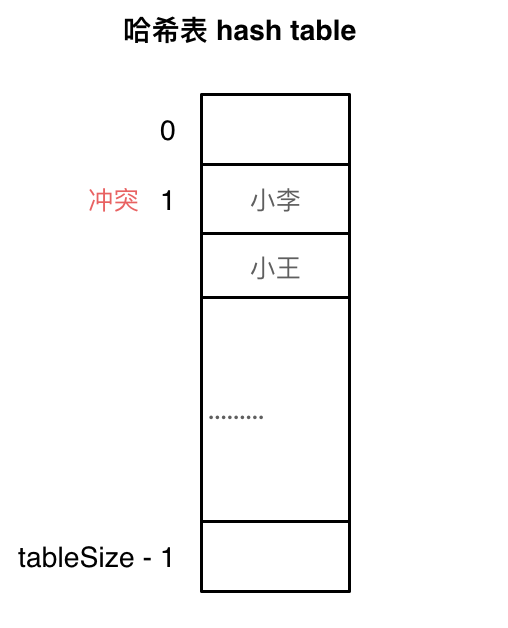
As shown in the figure, both Xiao Li and Xiao Wang map to the index at position 1, a phenomenon known as hash collision.
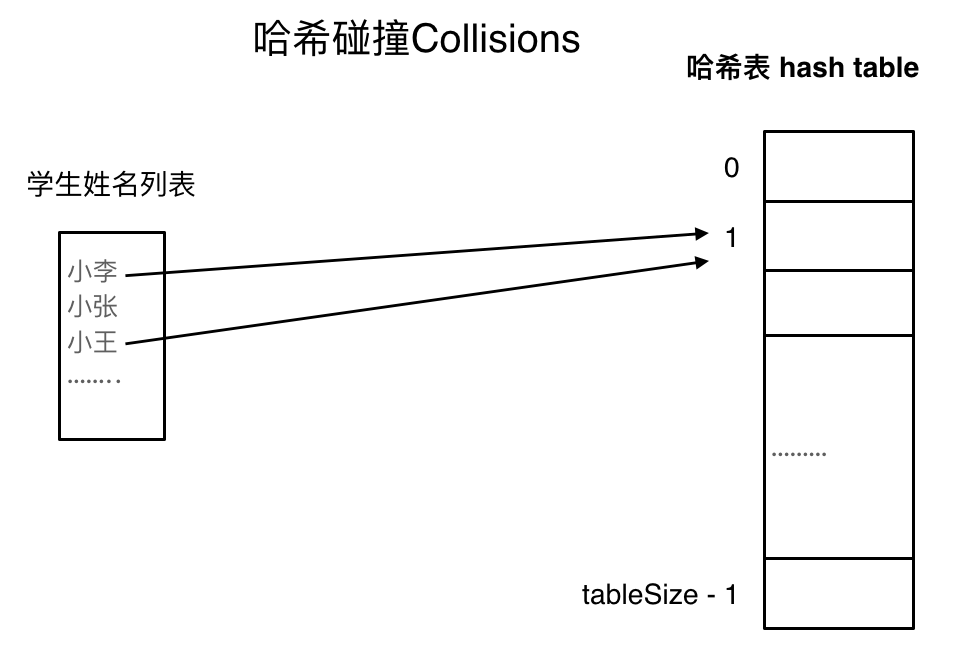
There are generally two methods to resolve hash collisions: chaining and linear probing.
# Chaining
In the example where Xiao Li and Xiao Wang collide at index 1, the conflicting elements are stored in a linked list. In this way, we can access both Xiao Li and Xiao Wang through the index.
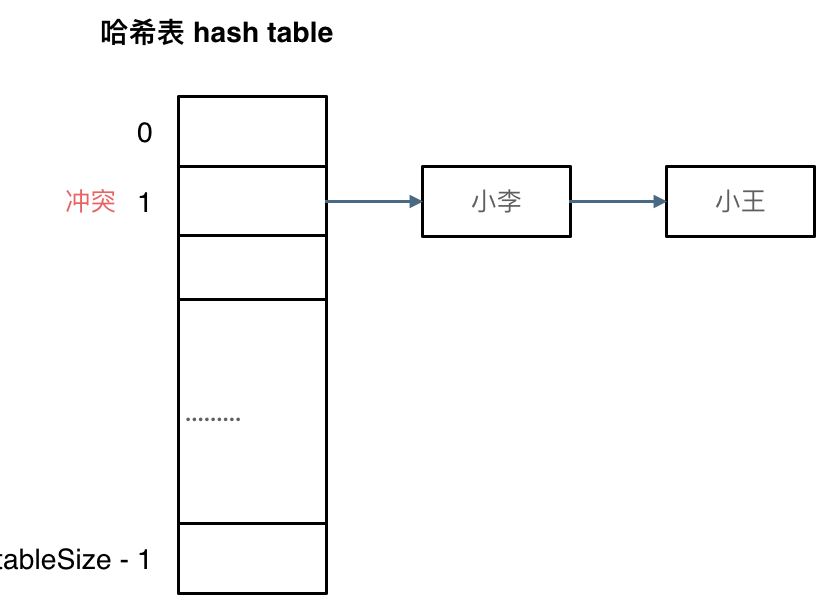
(With data size as dataSize and hash table size as tableSize)
Chaining essentially involves choosing an appropriate size for the hash table, preventing excessive empty values from wasting memory and avoiding long linked lists that would waste time in lookups.
# Linear Probing
For linear probing to work, the tableSize must be greater than dataSize. We need the empty slots in the hash table to resolve collisions.
For instance, if a collision occurs at a position occupied by Xiao Li, we keep searching for an empty slot to store Xiao Wang’s information. Thus, tableSize must be greater than dataSize, otherwise, there would be no empty slots to accommodate data collisions, as illustrated:
There are many more nuances to hash collisions that you can explore further if you’re interested. I won’t delve into those here.
# Three Common Structures for Hashing
When using hashing to solve a problem, we typically choose from the following three data structures:
- Array
- Set
- Map
There’s not much to say about arrays, so let’s look at sets.
In C++, set and map offer three data structures each, and their implementations and efficiencies are summarized in the table below:
| Collection Type | Implementation | Ordered | Duplicate Allowed | Mutable | Search Efficiency | Insert/Delete Efficiency |
|---|---|---|---|---|---|---|
std::set | Red-Black Tree | Ordered | No | No | O(log n) | O(log n) |
std::multiset | Red-Black Tree | Ordered | Yes | No | O(log n) | O(log n) |
std::unordered_set | Hash Table | Unordered | No | No | O(1) | O(1) |
std::unordered_set is implemented on top of a hash table, whereas std::set and std::multiset use a red-black tree for implementation. A red-black tree is a balanced binary search tree, thus key values are ordered, and the key cannot be modified as it would violate the tree's order, hence only addition and deletion are allowed.
| Map Type | Implementation | Ordered | Duplicate Keys Allowed | Mutable Keys | Search Efficiency | Insert/Delete Efficiency |
|---|---|---|---|---|---|---|
std::map | Red-Black Tree | Ordered | No | No | O(log n) | O(log n) |
std::multimap | Red-Black Tree | Ordered | Yes | No | O(log n) | O(log n) |
std::unordered_map | Hash Table | Unordered | No | No | O(1) | O(1) |
std::unordered_map is based on a hash table, while std::map and std::multimap utilize a red-black tree. Similarly, the key in std::map and std::multimap is ordered (a common interview question to test understanding of language container internals).
When using a set to solve a hash problem, prioritize unordered_set for its optimal search, insertion, and deletion efficiencies. If the collection needs to be ordered, use set. If both ordered and duplicate data are required, use multiset.
Looking at map, map uses a key-value structure where restrictions apply to key but not to value, because the storage of the key is based on a red-black tree.
This applies similarly to other languages like Java, with HashMap and TreeMap employing the same principles. This allows for flexible cross-language usage.
Although std::set and std::multiset are implemented using red-black trees rather than hash tables, they store and access data through the red-black tree. However, our use of these manifests in a hash function strategy—relying on the key (key) to access the value (value). Therefore, using these data structures in mapping solutions is still referred to as using a hash function. The same concept applies to std::map.
Here's an additional note: classical C++ literature such as "STL Source Code Analysis" refers to hash_set and hash_map. What relationship do they have with unordered_set and unordered_map?
Essentially, they serve the same function. However, unordered_set was officially introduced to the standard library in C++11, whereas hash_set wasn’t. Thus, it’s recommended to use unordered_set, as it’s officially certified. hash_set and hash_map were essentially solutions devised by enthusiasts before the C++11 standard.
# Summary
In summary, when the problem involves quickly determining if an element appears in a collection, consider using hashing.
Keep in mind, however, that hashing involves a trade-off of space for time. This is because additional arrays, sets, or maps are required to store data for quick lookups.
If you encounter scenarios in interview questions where you need to determine if an element has appeared, hashing should be your first consideration!
