# 78. Subsets
LeetCode Problem Link (opens new window)
Given a set of distinct integers, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.
Example: Input: nums = [1,2,3] Output:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
2
3
4
5
6
7
8
9
10
# Approach
The problem of finding subsets is different from 0077.Combinations (opens new window) and 131.Palindrome Partitioning (opens new window).
If you abstract the subsets problem, combinations problem, and partition problem as a tree, then both the combinations and partition problem involve collecting the leaf nodes of the tree, while the subsets problem requires finding all nodes of the tree!
In fact, subsets are also a form of the combinations problem since the order of elements in a subset does not matter. Subsets {1,2} and {2,1} are considered the same.
Since order does not matter and elements are not repeated, you should start the for loop in the backtracking algorithm from startIndex, not from 0!
You may ask, when can the for loop start from 0?
For permutation problems, you start from 0 because the sequence of elements matters, and permutations {1, 2} and {2, 1} are considered different. We will discuss permutation problems in upcoming articles.
Let's consider the example where nums = [1,2,3] and represent the search process in a tree-like structure:
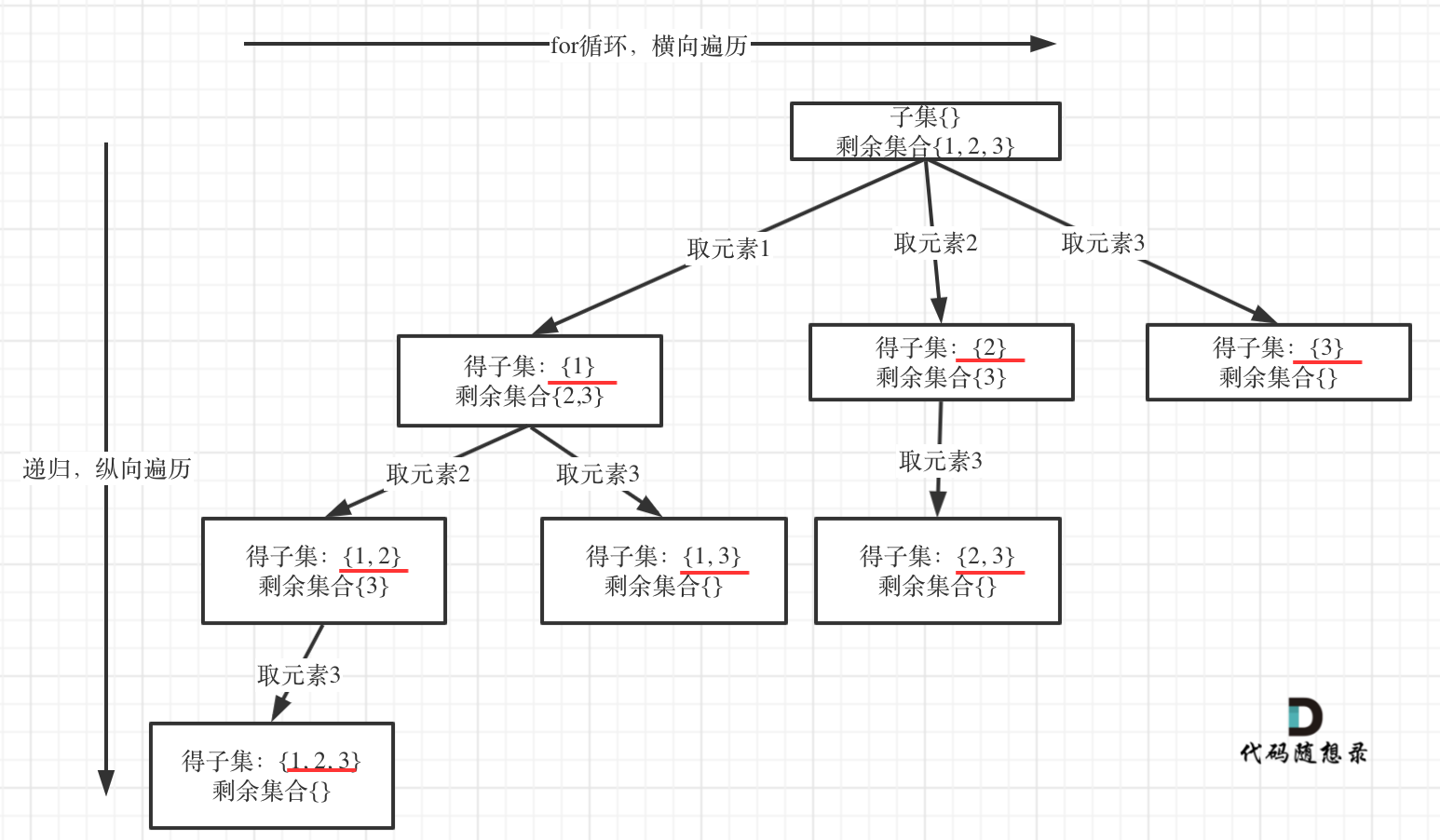
From the red-lined section of the diagram, you can see that if you traverse the tree and record all nodes, you will have the collection of all subsets.
# Three Steps of Backtracking
- Recursive function parameters:
Global variable array path for collecting subset elements, and a 2D array result to store the subset combinations. (These can also be included as parameters to the recursive function)
Parameters for the recursive function require startIndex.
Code:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
2
3
- Termination condition:
The diagram shows that:

The process ends when we reach an empty remaining set, which means a leaf node.
This happens when startIndex exceeds the length of the array. Code:
if (startIndex >= nums.size()) {
return;
}
2
3
In fact, you might not need a termination condition because when startIndex >= nums.size(), the for loop in the current level will naturally end.
- Single-level search logic:
There is no need for pruning with subset problems! Since subsets require you to traverse the entire tree.
The single-level recursive logic is as follows:
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]); // Collect elements for the subset
backtracking(nums, i + 1); // Proceed from i+1 to avoid duplicate elements
path.pop_back(); // Backtrack
}
2
3
4
5
Based on the given Backtracking Algorithm Fundamentals (opens new window) template:
void backtracking(parameters) {
if (termination condition) {
store results;
return;
}
for (choices in current layer) {
process node;
backtracking(path, choice list); // Recursion
backtrack, undo process
}
}
2
3
4
5
6
7
8
9
10
11
12
The C++ backtracking algorithm can be written as follows:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
result.push_back(path); // Collect subset before termination to avoid missing the current set
if (startIndex >= nums.size()) { // Termination condition is optional
return;
}
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> subsets(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
- Time complexity: O(n * 2^n)
- Space complexity: O(n)
In the comments, you may notice the termination condition can be omitted when the goal is to traverse the entire tree.
Some might worry about infinite recursion without a termination condition, but this is avoided since each recursion steps into the next level with i+1.
# Summary
After engaging with:
- Combination problems:
- Partition problems:
You'll find the subset problem simpler. This problem is a standard template problem.
However, it's crucial to understand the difference between the subset problem and the combination or partition problems. Subsets involve collecting all nodes from the tree structure.
Combination and partition problems involve collecting only the leaf nodes of the tree structure.
# Versions in Other Languages
# Java
class Solution {
List<List<Integer>> result = new ArrayList<>();// Collection for storing results satisfying the conditions
LinkedList<Integer> path = new LinkedList<>();// Used to store the result meeting conditions
public List<List<Integer>> subsets(int[] nums) {
subsetsHelper(nums, 0);
return result;
}
private void subsetsHelper(int[] nums, int startIndex){
result.add(new ArrayList<>(path));// "Record all nodes while traversing this tree, which forms the required subset set."
if (startIndex >= nums.length){ // termination condition can be omitted
return;
}
for (int i = startIndex; i < nums.length; i++){
path.add(nums[i]);
subsetsHelper(nums, i + 1);
path.removeLast();
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Python
class Solution:
def subsets(self, nums):
result = []
path = []
self.backtracking(nums, 0, path, result)
return result
def backtracking(self, nums, startIndex, path, result):
result.append(path[:]) # Collect subsets before termination to avoid missing the current set
# if startIndex >= len(nums): # Termination condition is optional
# return
for i in range(startIndex, len(nums)):
path.append(nums[i])
self.backtracking(nums, i + 1, path, result)
path.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Go
var (
path []int
res [][]int
)
func subsets(nums []int) [][]int {
res, path = make([][]int, 0), make([]int, 0, len(nums))
dfs(nums, 0)
return res
}
func dfs(nums []int, start int) {
tmp := make([]int, len(path))
copy(tmp, path)
res = append(res, tmp)
for i := start; i < len(nums); i++ {
path = append(path, nums[i])
dfs(nums, i+1)
path = path[:len(path)-1]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# JavaScript
var subsets = function(nums) {
let result = []
let path = []
function backtracking(startIndex) {
result.push([...path])
for(let i = startIndex; i < nums.length; i++) {
path.push(nums[i])
backtracking(i + 1)
path.pop()
}
}
backtracking(0)
return result
};
2
3
4
5
6
7
8
9
10
11
12
13
14
# TypeScript
function subsets(nums: number[]): number[][] {
const resArr: number[][] = [];
backTracking(nums, 0, []);
return resArr;
function backTracking(nums: number[], startIndex: number, route: number[]): void {
resArr.push([...route]);
let length = nums.length;
if (startIndex === length) return;
for (let i = startIndex; i < length; i++) {
route.push(nums[i]);
backTracking(nums, i + 1, route);
route.pop();
}
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Rust
Approach 1: Using the standard solution, recursive backtracking.
impl Solution {
fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, nums: &Vec<i32>, start_index: usize) {
result.push(path.clone());
let len = nums.len();
// if start_index >= len { return; }
for i in start_index..len {
path.push(nums[i]);
Self::backtracking(result, path, nums, i + 1);
path.pop();
}
}
pub fn subsets(nums: Vec<i32>) -> Vec<Vec<i32>> {
let mut result: Vec<Vec<i32>> = Vec::new();
let mut path: Vec<i32> = Vec::new();
Self::backtracking(&mut result, &mut path, &nums, 0);
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Approach 2: Use binary enumeration. The subset problem for n elements has $2^n$ possible outcomes. If we use a binary number where each bit represents the decision to include or not include the corresponding element, it results in $2^n$ combinations, perfectly aligned with the subset possibilities. Thus, we can use this loop enumeration effectively without recursion.
impl Solution {
pub fn subsets(nums: Vec<i32>) -> Vec<Vec<i32>> {
let n = nums.len();
let mut result = Vec::with_capacity(1 << n);
for i in 0..(1 << n) {
let mut subset = Vec::new();
for j in 0..n {
if i & (1 << j) != 0 {
subset.push(nums[j]);
}
}
result.push(subset);
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# C
int* path;
int pathTop;
int** ans;
int ansTop;
// Record the length of each one-dimensional array in the 2D array
int* length;
// Copy the current path array to ans
void copy() {
int* tempPath = (int*)malloc(sizeof(int) * pathTop);
int i;
for(i = 0; i < pathTop; i++) {
tempPath[i] = path[i];
}
ans = (int**)realloc(ans, sizeof(int*) * (ansTop+1));
length[ansTop] = pathTop;
ans[ansTop++] = tempPath;
}
void backTracking(int* nums, int numsSize, int startIndex) {
copy();
if(startIndex >= numsSize) {
return;
}
int j;
for(j = startIndex; j < numsSize; j++) {
path[pathTop++] = nums[j];
backTracking(nums, numsSize, j+1);
pathTop--;
}
}
int** subsets(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
path = (int*)malloc(sizeof(int) * numsSize);
ans = (int**)malloc(0);
length = (int*)malloc(sizeof(int) * 1500);
ansTop = pathTop = 0;
backTracking(nums, numsSize, 0);
*returnSize = ansTop;
*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
int i;
for(i = 0; i < ansTop; i++) {
(*returnColumnSizes)[i] = length[i];
}
return ans;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Swift
func subsets(_ nums: [Int]) -> [[Int]] {
var result = [[Int]]()
var path = [Int]()
func backtracking(startIndex: Int) {
result.append(path)
let end = nums.count
guard startIndex < end else { return }
for i in startIndex ..< end {
path.append(nums[i])
backtracking(startIndex: i + 1)
path.removeLast()
}
}
backtracking(startIndex: 0)
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Scala
Approach 1: Using the provided approach of this problem
object Solution {
import scala.collection.mutable
def subsets(nums: Array[Int]): List[List[Int]] = {
var result = mutable.ListBuffer[List[Int]]()
var path = mutable.ListBuffer[Int]()
def backtracking(startIndex: Int): Unit = {
result.append(path.toList)
if (startIndex >= nums.size) {
return
}
for (i <- startIndex until nums.size) {
path.append(nums(i))
backtracking(i + 1)
path.remove(path.size - 1)
}
}
backtracking(0)
result.toList
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Approach 2: Transform the problem into a binary tree, for each element there are select or not select two choices. Until the end of traversal, all leaf nodes are the answer:
object Solution {
import scala.collection.mutable
def subsets(nums: Array[Int]): List[List[Int]] = {
var result = mutable.ListBuffer[List[Int]]()
def backtracking(path: mutable.ListBuffer[Int], startIndex: Int): Unit = {
if (startIndex == nums.length) {
result.append(path.toList)
return
}
path.append(nums(startIndex))
backtracking(path, startIndex + 1) // Select the element
path.remove(path.size - 1)
backtracking(path, startIndex + 1) // Don't select the element
}
backtracking(mutable.ListBuffer[Int](), 0)
result.toList
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# C#
public class Solution {
public IList<IList<int>> res = new List<IList<int>>();
public IList<int> path = new List<int>();
public IList<IList<int>> Subsets(int[] nums) {
BackTracking(nums, 0);
return res;
}
public void BackTracking(int[] nums, int start){
res.Add(new List<int>(path));
if(start > nums.Length) return;
for (int i = start; i < nums.Length; i++)
{
path.Add(nums[i]);
BackTracking(nums, i + 1);
path.RemoveAt(path.Count - 1);
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
