40. Combination Sum II

LeetCode Problem Link (opens new window)

Given a collection of candidate numbers (candidates) and a target number (target), find all unique combinations in candidates where the candidate numbers sum to target.

Each number in candidates may only be used once in the combination.

Note: All numbers (including target) are positive integers. The solution set must not contain duplicate combinations.

• Example 1:
• Input: candidates = [10,1,2,7,6,1,5], target = 8,
• The solution set is:

[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

• Example 2:
• Input: candidates = [2,5,2,1,2], target = 5,
• The solution set is:

[
  [1, 2, 2],
  [5]
]

Explanation

This problem differs from 0039.Combination Sum (opens new window) in the following ways:

1. Each number in candidates can only be used once in each combination.
2. The array candidates in this problem may contain duplicate numbers, unlike 0039.Combination Sum (opens new window), which does not have duplicates.

Finally, this problem requires that the solution set must not contain duplicate combinations, the same requirement as 0039.Combination Sum (opens new window).

The main difficulty of this problem lies in the fact that the set (candidates) has duplicate elements, yet the solution set must not contain duplicate combinations.

Some might think of generating all combinations and then using a set or map to remove duplicates. This approach is likely to result in a timeout.

Therefore, duplicates must be handled during the search process itself.

Many find the de-duplication strategy hard to understand, and many solutions online do not clarify it — they might give code that works, but without a clear explanation, often suggesting to simply "remove duplicates."

The reason why duplication is hard to understand is that "duplicate removal" essentially means that already "used" elements cannot be picked again. Once stated this way, it seems straightforward!

Combinatorial problems can be abstracted into tree structures, where "used" appears in two dimensions: "used on the same tree branch" and "used on the same tree level." Failure to understand these two dimensions is what prevents many from fully grasping the de-duplication logic.

The question is whether elements should be considered "used" on the same tree level or on the same tree branch.

If we read the problem again, elements can be repeated within the same combination, but two combinations should not be identical.

Thus, the de-duplication focuses on "used" across the same tree level, as elements on the same branch belong to the same combination and do not need to be de-duplicated.

For clarity, let's consider an example: candidates = [1, 1, 2], target = 3 (for simplicity, assume candidates is already sorted).

If you focus on de-duplication across the tree level, the array must be sorted!

The selection process can be represented as a tree structure:

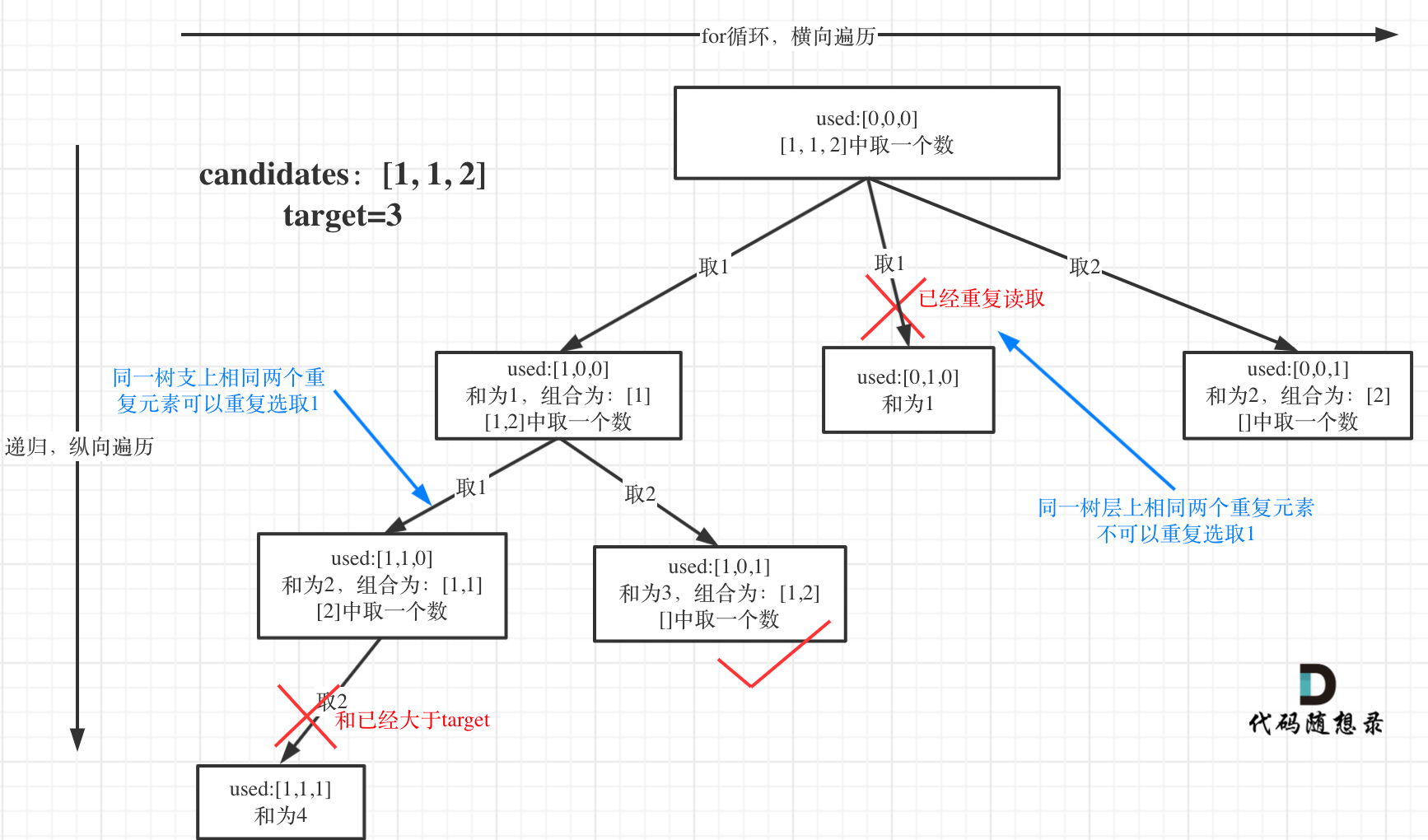
Note that I added an used array in addition to what's needed for 0039.Combination Sum (opens new window). This used array will be crucial in the following discussion.

Backtracking in Three Steps

• Function Parameters

Similar to 0039.Combination Sum (opens new window), this requires an additional bool array used to track whether elements on the same branch have been used.

The task of removing duplicate combinations is accomplished by used.

The code is as follows:

vector<vector<int>> result; // Holds the combinations
vector<int> path;           // Holds the current combination
void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {

• Base Case for Termination

As in 0039.Combination Sum (opens new window), termination conditions are sum > target and sum == target.

The code is as follows:

if (sum > target) { // This condition can actually be omitted
    return;
}
if (sum == target) {
    result.push_back(path);
    return;
}

The condition sum > target can indeed be omitted because pruning will occur during the recursive single-layer iteration, to be discussed later.

• Single-layer Recursive Logic

The main difference from 0039.Combination Sum (opens new window) is in handling duplicates.

Earlier, we noted: de-duplication is concerned with elements "used" within the same tree level. How do we determine if an element has been "used" (identical element) at the same tree level?

If candidates[i] == candidates[i - 1] and used[i - 1] == false, it indicates that the previous branch used candidates[i - 1], i.e., candidates[i - 1] was used at the same tree level.

In this case, the loop should continue.

This part can be quite abstract; consider the diagram:

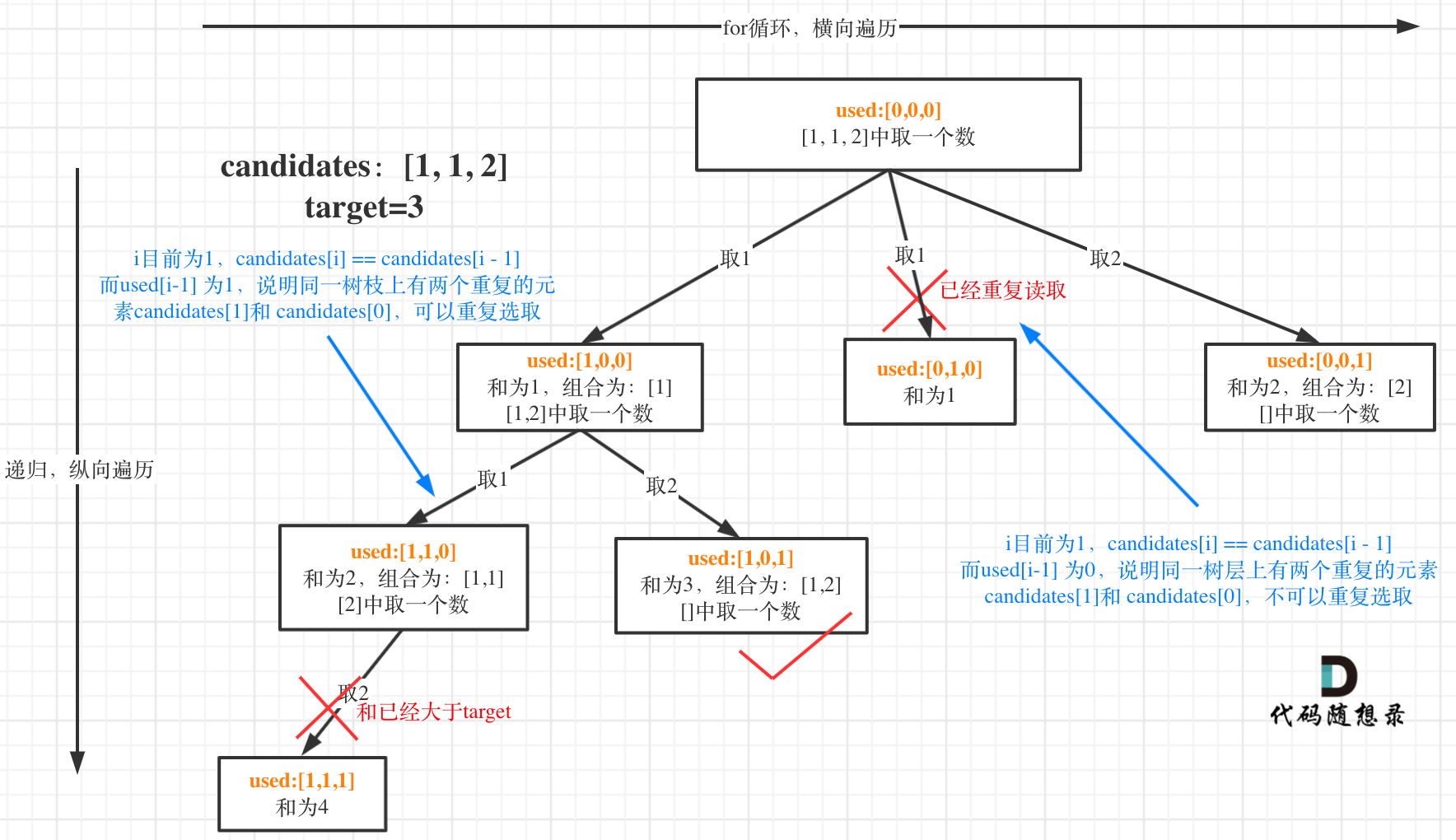
In the diagram, I marked the change to used in orange. You can see, in the case of candidates[i] == candidates[i - 1]:

• used[i - 1] == true indicates that candidates[i - 1] was used on the same tree branch.
• used[i - 1] == false indicates that candidates[i - 1] was used on the same tree level.

Some might wonder why is used[i - 1] == false indicative of the same tree level. It's because, on the same tree level, used[i - 1] == false means that the current candidates[i] is a result of backtracking from candidates[i - 1].

Conversely, used[i - 1] == true indicates moving into the next layer of recursion along a branch, as shown:

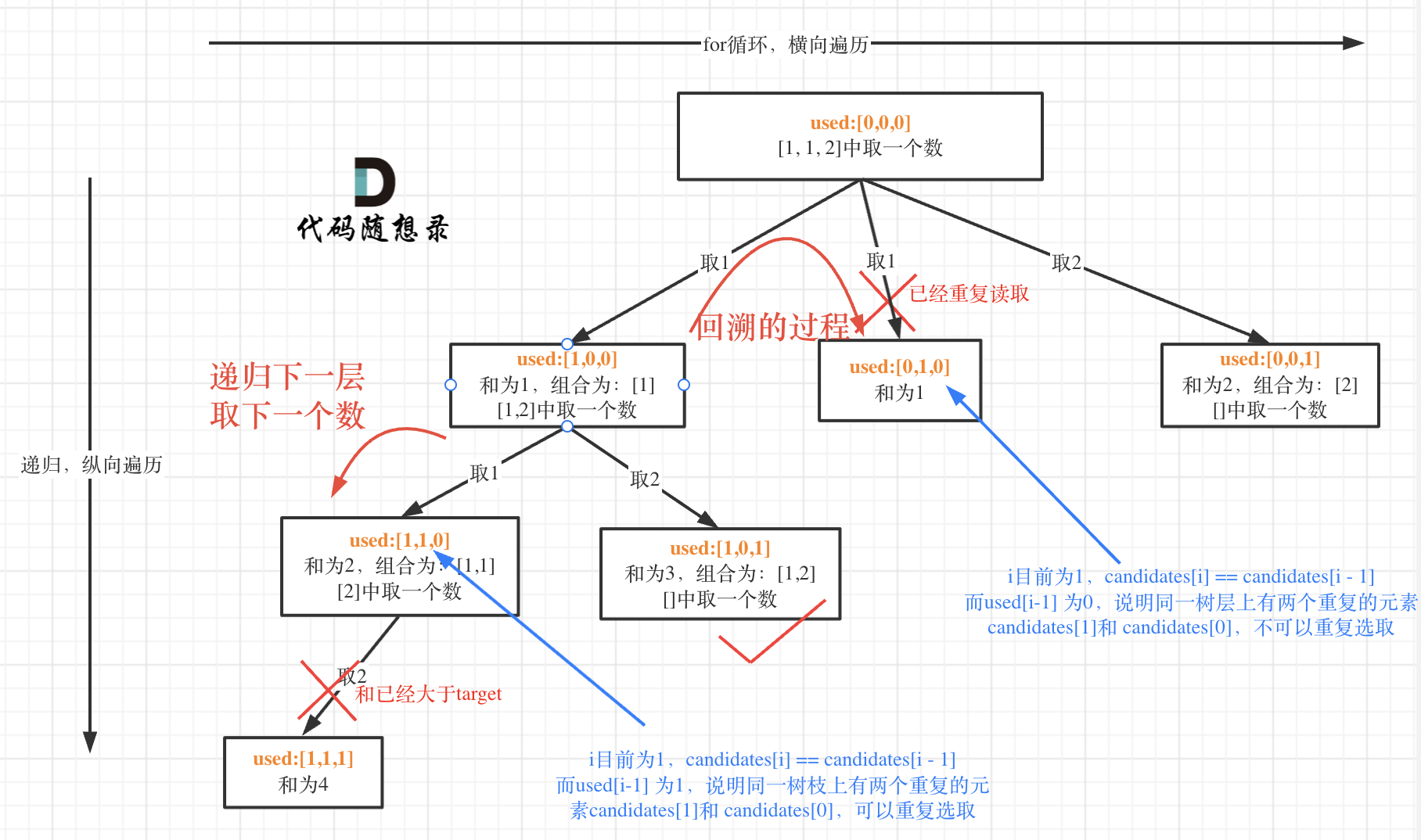
This logic of de-duplication is quite abstract, and it's rare to find online explanations that clarify it completely. Having addressed this issue, our discussion should now feel much more integrated and comprehensive!

The code for the single-layer search logic is as follows:

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
    // used[i - 1] == true means candidates[i - 1] has been used on the same branch
    // used[i - 1] == false means candidates[i - 1] has been used on the same level
    // Skip elements that were used on the same level
    if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
        continue;
    }
    sum += candidates[i];
    path.push_back(candidates[i]);
    used[i] = true;
    backtracking(candidates, target, sum, i + 1, used); // Difference 1 from Combination Sum: here is i+1 because each number can only be used once
    used[i] = false;
    sum -= candidates[i];
    path.pop_back();
}

Note that sum + candidates[i] <= target is a pruning operation, as explained in 0039.Combination Sum (opens new window)!

After analyzing the three steps of backtracking, the complete C++ code is as follows:

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            // used[i - 1] == true means candidates[i - 1] was used on the same branch
            // used[i - 1] == false means candidates[i - 1] was used on the same level
            // Skip elements that were utilized on the same level
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
                continue;
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, sum, i + 1, used); // Difference 1 from Combination Sum: here is i+1 because each number can only be used once
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }

public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        vector<bool> used(candidates.size(), false);
        path.clear();
        result.clear();
        // First sort candidates to get duplicate elements adjacent.
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0, used);
        return result;
    }
};

• Time Complexity: O(n * 2^n)
• Space Complexity: O(n)

Additional Note

You can also handle de-duplication directly with the startIndex without using the used array.

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            // Skip elements that were used on the same level
            if (i > startIndex && candidates[i] == candidates[i - 1]) {
                continue;
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i + 1); // Difference 1 from Combination Sum: here is i+1 because each number can only be used once
            sum -= candidates[i];
            path.pop_back();
        }
    }

public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        path.clear();
        result.clear();
        // First sort candidates to get duplicate elements adjacent.
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

Summary

This problem, while seemingly similar to 0039.Combination Sum (opens new window), becomes more challenging because candidates can contain duplicate elements and the solution requires no duplicate combinations.

The crux is in the de-duplication logic. The code is straightforward and readily available online, but few sources clarify the code's logic or justify the approach. Most mention "removing duplicates" without detailing the mechanics.

That's why Carl felt the need to thoroughly clarify the process of de-duplication, even inventing terms like "tree level de-duplication" and "tree branch de-duplication" to enhance comprehension.

Code Versions in Other Languages

Java

With Marked Array

class Solution {
  LinkedList<Integer> path = new LinkedList<>();
  List<List<Integer>> ans = new ArrayList<>();
  boolean[] used;
  int sum = 0;

  public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    used = new boolean[candidates.length];
    // Add marking array to assist in determining same-level node traversal
    Arrays.fill(used, false);
    // Sort the array to group duplicate numbers together
    Arrays.sort(candidates);
    backTracking(candidates, target, 0);
    return ans;
  }

  private void backTracking(int[] candidates, int target, int startIndex) {
    if (sum == target) {
      ans.add(new ArrayList(path));
    }
    for (int i = startIndex; i < candidates.length; i++) {
      if (sum + candidates[i] > target) {
        break;
      }
      // For duplicate nodes, skip if the first node of the level has been visited
      if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
        continue;
      }
      used[i] = true;
      sum += candidates[i];
      path.add(candidates[i]);
      // Each node can only be chosen once, so start from next position
      backTracking(candidates, target, i + 1);
      used[i] = false;
      sum -= candidates[i];
      path.removeLast();
    }
  }
}

Without Marked Array

class Solution {
  List<List<Integer>> res = new ArrayList<>();
  LinkedList<Integer> path = new LinkedList<>();
  int sum = 0;
  
  public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    // To group the same numbers together, sort first
    Arrays.sort(candidates);
    backTracking(candidates, target, 0);
    return res;
  }
  
  private void backTracking(int[] candidates, int target, int start) {
    if (sum == target) {
      res.add(new ArrayList<>(path));
      return;
    }
    for (int i = start; i < candidates.length && sum + candidates[i] <= target; i++) {
      // Correct way to skip duplicates
      // Skip elements used at the same level
      if (i > start && candidates[i] == candidates[i - 1]) {
        continue;
      }

      sum += candidates[i];
      path.add(candidates[i]);
      // i+1 means each group can select the element only once
      backTracking(candidates, target, i + 1);

      int temp = path.getLast();
      sum -= temp;
      path.removeLast();
    }
  }
}

Python

Backtracking

class Solution:
    def backtracking(self, candidates, target, total, startIndex, path, result):
        if total == target:
            result.append(path[:])
            return

        for i in range(startIndex, len(candidates)):
            if i > startIndex and candidates[i] == candidates[i - 1]:
                continue

            if total + candidates[i] > target:
                break

            total += candidates[i]
            path.append(candidates[i])
            self.backtracking(candidates, target, total, i + 1, path, result)
            total -= candidates[i]
            path.pop()

    def combinationSum2(self, candidates, target):
        result = []
        candidates.sort()
        self.backtracking(candidates, target, 0, 0, [], result)
        return result

Backtracking with used

class Solution:
    def backtracking(self, candidates, target, total, startIndex, used, path, result):
        if total == target:
            result.append(path[:])
            return

        for i in range(startIndex, len(candidates)):
            # Skip the duplicates that appear on the same level
            if i > startIndex and candidates[i] == candidates[i - 1] and not used[i - 1]:
                continue

            if total + candidates[i] > target:
                break

            total += candidates[i]
            path.append(candidates[i])
            used[i] = True
            self.backtracking(candidates, target, total, i + 1, used, path, result)
            used[i] = False
            total -= candidates[i]
            path.pop()

    def combinationSum2(self, candidates, target):
        used = [False] * len(candidates)
        result = []
        candidates.sort()
        self.backtracking(candidates, target, 0, 0, used, [], result)
        return result

Optimized Backtracking

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        results = []
        self.combinationSumHelper(candidates, target, 0, [], results)
        return results

    def combinationSumHelper(self, candidates, target, index, path, results):
        if target == 0:
            results.append(path[:])
            return
        for i in range(index, len(candidates)):
            if i > index and candidates[i] == candidates[i - 1]:
                continue  
            if candidates[i] > target:
                break  
            path.append(candidates[i])
            self.combinationSumHelper(candidates, target - candidates[i], i + 1, path, results)
            path.pop()

Go

The focus is on removing duplicates during backtracking

Using used array

var (
    res [][]int
    path  []int
    used  []bool
)
func combinationSum2(candidates []int, target int) [][]int {
    res, path = make([][]int, 0), make([]int, 0, len(candidates))
    used = make([]bool, len(candidates))
    sort.Ints(candidates)   // Sort for pruning
    dfs(candidates, 0, target)
    return res
}

func dfs(candidates []int, start int, target int) {
    if target == 0 {   // If target continuously decreases to 0, we've met the target
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }
    for i := start; i < len(candidates); i++ {
        if candidates[i] > target {  // Prune early
            break
        }
        // i > start limits this to prevent duplicate solutions reaching a depth-first tree
        if i > 0 && candidates[i] == candidates[i-1] && !used[i-1] { 
            continue
        }
        path = append(path, candidates[i])
        used[i] = true
        dfs(candidates, i+1, target - candidates[i])
        used[i] = false
        path = path[:len(path) - 1]
    }
}

Without used array

var (
    res [][]int
    path  []int
)
func combinationSum2(candidates []int, target int) [][]int {
    res, path = make([][]int, 0), make([]int, 0, len(candidates))
    sort.Ints(candidates)   // Sort for pruning
    dfs(candidates, 0, target)
    return res
}

func dfs(candidates []int, start int, target int) {
    if target == 0 {   // If target continuously decreases to 0, we've met the target
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }
    for i := start; i < len(candidates); i++ {
        if candidates[i] > target {  // Prune early
            break
        }
        // i != start limits depth traversal from duplicates
        if i != start && candidates[i] == candidates[i-1] { // Remove duplicates
            continue
        }
        path = append(path, candidates[i])
        dfs(candidates, i+1, target - candidates[i])
        path = path[:len(path) - 1]
    }
}

JavaScript

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function(candidates, target) {
    const res = []; path = [], len = candidates.length;
    candidates.sort((a,b)=>a-b);
    backtracking(0, 0);
    return res;
    function backtracking(sum, i) {
        if (sum === target) {
            res.push(Array.from(path));
            return;
        }
        for(let j = i; j < len; j++) {
            const n = candidates[j];
            if(j > i && candidates[j] === candidates[j-1]){
              // If current element is same as previous, same-level means it can be skipped
              continue;
            }
            // If current element exceeds target-sum, any further can't meet condition
            // break ends current recursion
            if(n > target - sum) break;
            path.push(n);
            sum += n;
            backtracking(sum, j + 1);
            path.pop();
            sum -= n;
        }
    }
};

Using used for duplicates

var combinationSum2 = function(candidates, target) {
    let res = [];
    let path = [];
    let total = 0;
    const len = candidates.length;
    candidates.sort((a, b) => a - b);
    let used = new Array(len).fill(false);
    const backtracking = (startIndex) => {
        if (total === target) {
            res.push([...path]);
            return;
        }
        for(let i = startIndex; i < len && total < target; i++) {
            const cur = candidates[i];
            if (cur > target - total || (i > 0 && cur === candidates[i - 1] && !used[i - 1])) continue;
            path.push(cur);
            total += cur;
            used[i] = true;
            backtracking(i + 1);
            path.pop();
            total -= cur;
            used[i] = false;
        }
    }
    backtracking(0);
    return res;
};

TypeScript

function combinationSum2(candidates: number[], target: number): number[][] {
    candidates.sort((a, b) => a - b);
    const resArr: number[][] = [];
    function backTracking(
        candidates: number[], target: number,
        curSum: number, startIndex: number, route: number[]
    ) {
        if (curSum > target) return;
        if (curSum === target) {
            resArr.push(route.slice());
            return;
        }
        for (let i = startIndex, length = candidates.length; i < length; i++) {
            if (i > startIndex && candidates[i] === candidates[i - 1]) {
                continue;
            }
            let tempVal: number = candidates[i];
            route.push(tempVal);
            backTracking(candidates, target, curSum + tempVal, i + 1, route);
            route.pop();

        }
    }
    backTracking(candidates, target, 0, 0, []);
    return resArr;
};

Rust

impl Solution {
    pub fn backtracking(result: &mut Vec<Vec<i32>>, path: &mut Vec<i32>, candidates: &Vec<i32>, target: i32, mut sum: i32, start_index: usize, used: &mut Vec<bool>) {
        if sum == target {
            result.push(path.to_vec());
            return;
        }
        for i in start_index..candidates.len() {
            if sum + candidates[i] <= target {
                if i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false { continue; }
                sum += candidates[i];
                path.push(candidates[i]);
                used[i] = true;
                Self::backtracking(result, path, candidates, target, sum, i + 1, used);
                used[i] = false;
                sum -= candidates[i];
                path.pop();
            }
        }
    }

    pub fn combination_sum2(candidates: Vec<i32>, target: i32) -> Vec<Vec<i32>> {
        let mut result: Vec<Vec<i32>> = Vec::new();
        let mut path: Vec<i32> = Vec::new();
        let mut used: Vec<bool> = vec![false; candidates.len()];
        let mut candidates = candidates;
        candidates.sort();
        Self::backtracking(&mut result, &mut path, &candidates, target, 0, 0, &mut used);
        result
    }
}

C

int* path;
int pathTop;
int** ans;
int ansTop;
// Record the size of each one-dimensional array in ans
int* length;
int cmp(const void* a1, const void* a2) {
    return *((int*)a1) - *((int*)a2);
}

void backTracking(int* candidates, int candidatesSize,  int target, int sum, int startIndex) {
    if(sum >= target) {
        // If sum equals target, copy current path
        if(sum == target) {
            int* tempPath = (int*)malloc(sizeof(int) * pathTop);
            int j;
            for(j = 0; j < pathTop; j++) {
                tempPath[j] = path[j];
            }
            length[ansTop] = pathTop;
            ans[ansTop++] = tempPath;
        }
        return ;
    }

    int i;
    for(i = startIndex; i < candidatesSize; i++) {
        // Skip used elements on the same tree level
        if(i > startIndex && candidates[i] == candidates[i-1])
            continue;
        path[pathTop++] = candidates[i];
        sum += candidates[i];
        backTracking(candidates, candidatesSize, target, sum, i + 1);
        // Backtrack
        sum -= candidates[i];
        pathTop--;
    }
}

int** combinationSum2(int* candidates, int candidatesSize, int target, int* returnSize, int** returnColumnSizes){
    path = (int*)malloc(sizeof(int) * 50);
    ans = (int**)malloc(sizeof(int*) * 100);
    length = (int*)malloc(sizeof(int) * 100);
    pathTop = ansTop = 0;
    // Quick sort for the purpose of grouping duplicate elements together
    qsort(candidates, candidatesSize, sizeof(int), cmp);

    backTracking(candidates, candidatesSize, target, 0, 0);

    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = length[i];
    }
    return ans;
}

Swift

func combinationSum2(_ candidates: [Int], _ target: Int) -> [[Int]] {
    // To facilitate removing duplicates, sort the collection first
    let candidates = candidates.sorted()
    var result = [[Int]]()
    var path = [Int]()
    func backtracking(sum: Int, startIndex: Int) {
        // Termination condition
        if sum == target {
            result.append(path)
            return
        }

        let end = candidates.count
        guard startIndex < end else { return }
        for i in startIndex ..< end {
            if i > startIndex, candidates[i] == candidates[i - 1] { continue } // Skip duplicates
            let sum = sum + candidates[i] // Use local variables to encapsulate backtracking
            if sum > target { continue } // Prune

            path.append(candidates[i]) // Process
            backtracking(sum: sum, startIndex: i + 1) // i+1 avoids duplicate access
            path.removeLast() // Backtrack
        }
    }
    backtracking(sum: 0, startIndex: 0)
    return result
}

Scala

object Solution {
  import scala.collection.mutable    
  def combinationSum2(candidates: Array[Int], target: Int): List[List[Int]] = {
    var res = mutable.ListBuffer[List[Int]]()
    var path = mutable.ListBuffer[Int]()
    var candidate = candidates.sorted

    def backtracking(sum: Int, startIndex: Int): Unit = {
      if (sum == target) {
        res.append(path.toList)
        return
      }

      for (i <- startIndex until candidate.size if sum + candidate(i) <= target) {
        if (!(i > startIndex && candidate(i) == candidate(i - 1))) {
          path.append(candidate(i))
          backtracking(sum + candidate(i), i + 1)
          path = path.take(path.size - 1)
        }
      }
    }

    backtracking(0, 0)
    res.toList
  }
}

C#

public class Solution
{
    public List<IList<int>> res = new List<IList<int>>();
    public List<int> path = new List<int>();
    public IList<IList<int>> CombinationSum2(int[] candidates, int target)
    {

        Array.Sort(candidates);
        BackTracking(candidates, target, 0, 0);
        return res;
    }
    public void BackTracking(int[] candidates, int target, int start, int sum)
    {
        if (sum > target) return;
        if (sum == target)
        {
            res.Add(new List<int>(path));
            return;
        }
        for (int i = start; i < candidates.Length && sum + candidates[i] <= target; i++)
        {
            if (i > start && candidates[i] == candidates[i - 1]) continue;
            sum += candidates[i];
            path.Add(candidates[i]);
            BackTracking(candidates, target, i + 1, sum);
            sum -= candidates[i];
            path.RemoveAt(path.Count - 1);
        }
    }
}