Greedy Algorithm: Reconstruct Queue by Height (Sequel)

In the explanation of 0406.Queue Reconstruction by Height (opens new window), we mentioned that using a vector (dynamic array in C++) for the insert operation is time-consuming.

Here, we will dedicate an article to discuss this issue in detail.

The code using vector is as follows:

// Version 1, using vector (dynamic array)
class Solution {
public:
    static bool cmp(const vector<int> a, const vector<int> b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);
        vector<vector<int>> que;
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1];
            que.insert(que.begin() + position, people[i]);
        }
        return que;
    }
};

Time consumption is as follows:

Intuitively, the insert operation for an array is O(n), so the overall time complexity of the code is O(n^2).

On analysis, it seems similar to the time complexity of the version implemented with a linked list, so why is there such a significant efficiency difference upon submission?

// Version 2, using list (linked list)
class Solution {
public:
    // Sort by height in descending order (if height is the same, sort by k in ascending order)
    static bool cmp(const vector<int> a, const vector<int> b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);
        list<vector<int>> que; // list is implemented as a linked list, making insertion much more efficient than vector
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1]; // Insert at index position
            std::list<vector<int>>::iterator it = que.begin();
            while (position--) { // Find the insertion position
                it++;
            }
            que.insert(it, people[i]);
        }
        return vector<vector<int>>(que.begin(), que.end());
    }
};

Time consumption is as follows:

As everyone knows, for a regular array, once the size is defined, it cannot be changed, for example, int a[10];, this array a can hold at most 10 elements, and it cannot be changed.

For a dynamic array, you don’t need to worry about the initial size, and you can freely add data to it. The reason for the time consumption lies in the underlying implementation of the dynamic array.

Why can a dynamic array be unrestricted by the initial size and allow you to freely push back data?

Firstly, the underlying implementation of vector is also a regular array.

The size of the vector has two dimensions: one is size, and the other is capacity. Size is what we usually use to iterate through a vector, for example:

for (int i = 0; i < vec.size(); i++) {

}

Capacity, however, is the size of the underlying array (which is just a regular array). Capacity doesn’t necessarily equal size.

When inserting data, if the size exceeds capacity, the capacity will expand exponentially, but the size exposed externally will only increase by 1.

How is the vector expanded when its underlying implementation is a regular array?

It requests a new array which is twice the size of the original one, copies the data over, and releases the memory of the original array. (Yes, it's done in such a straightforward and crude way!)

To illustrate with an example, as shown:

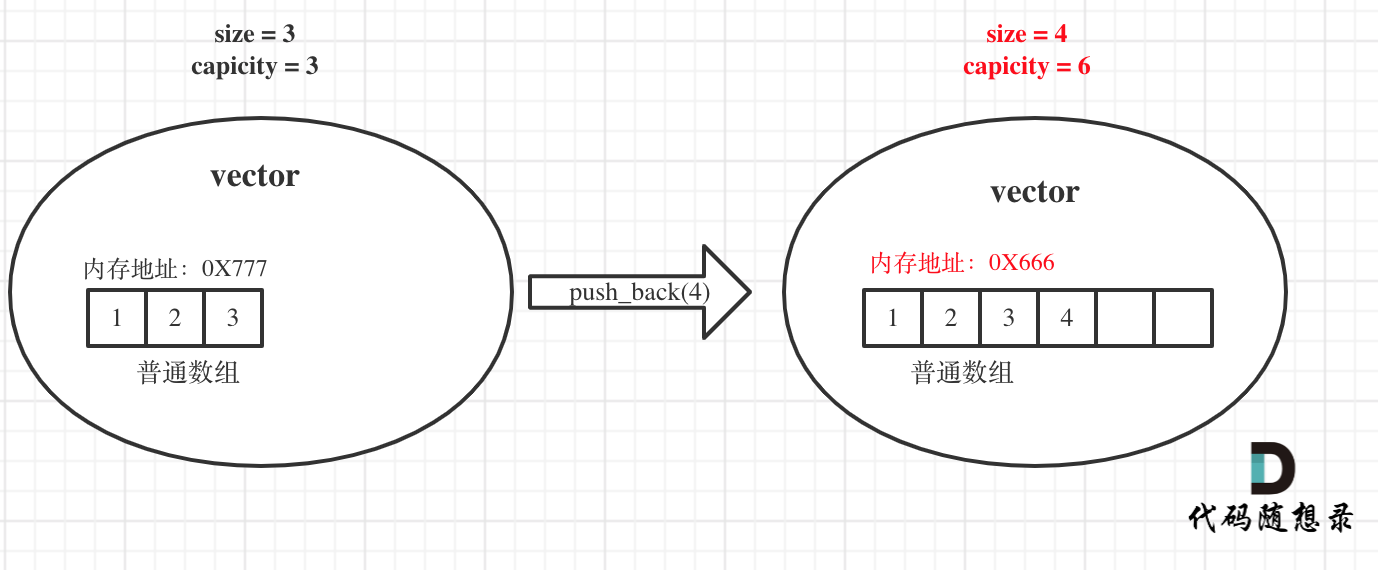
In the original vector, both size and capacity are 3, initialized as 1 2 3. Now, we want to push_back an element 4.

So, the underlying implementation requests a new regular array with size 6, and copies the original elements over, freeing the memory of the original array. Note that the starting address of the underlying array has changed in the diagram.

Also pay attention to the change in capacity and size, I’ve highlighted key areas in red.

And in 0406.Queue Reconstruction by Height (opens new window), we used a vector for insert operations. You may note that although the apparent complexity is O(n^2), we don't know how many additional full copy operations are performed by the underlying implementation, so considering the underlying vector copy, the overall time complexity can be considered O(n^2 + t × n), where t is the number of underlying copy operations.

So, can we determine the size of the vector in advance to prevent dynamic expansion, given that in 0406.Queue Reconstruction by Height (opens new window) we already know there are as many people as people.size()? We could define a fixed-size vector, so we can control the vector to prevent dynamic expansion.

This method requires manually simulating the insert operation, which is not as straightforward as directly calling the insert interface, and it's not very efficient either!

The manual simulation process is not very simple and involves many details. I've roughly written a version, as follows:

// Version 3
// Using vector, but without dynamic expansion
class Solution {
public:
    static bool cmp(const vector<int> a, const vector<int> b) {
        if (a[0] == b[0]) return a[1] < b[1];
        return a[0] > b[0];
    }
    vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
        sort (people.begin(), people.end(), cmp);
        vector<vector<int>> que(people.size(), vector<int>(2, -1));
        for (int i = 0; i < people.size(); i++) {
            int position = people[i][1];
            if (position == que.size() - 1) que[position] = people[i];
            else { // Shift elements backward for insertion
                for (int j = que.size() - 2; j >= position; j--) que[j + 1] = que[j];
                que[position] = people[i];
            }
        }
        return que;
    }
};

Time consumption is as follows:

This code doesn't allow vector dynamic expansion, and we simulate the insert operation ourselves throughout. You can see it's clearly an O(n^2) method.

But the time recorded by LeetCode shows it’s even longer than Version 1, why is that, considering we have prevented the vector from dynamic expansion?

On one hand, LeetCode’s time recording isn't very precise, and results can swing significantly, so it only provides a rough measure.

On the other hand, even though we’ve prevented vector's underlying expansion, this fixed-size array requires shifting and assignment operations, which might be more frequent than the shifting and assignments done in Method 1, even when accounting for occasional expansions.

In Method 1, the array starts small, so the number of element shifts when inserting isn't that large, even with occasional expansions, whereas in Version 3, each insertion requires shifting the elements for the maximum array size.

Thus, it’s hard to determine which one is superior between the two array-based methods, Method 1 and Method 3, but both are less efficient compared to Method 2 using a linked list!

After a thorough analysis, for 0406.Queue Reconstruction by Height (opens new window), it’s better to use a linked list! Don't bother experimenting further, consider it a favor that I’ve experimented for you.

Summary

You may have realized that the insert or delete operations on a standard container in a programming language can significantly impact the algorithm you write!

If you disregard the language when discussing algorithms, unless you never use code to write algorithms purely for analysis, otherwise, insufficient language expertise can lead you to write O(n^2) performance from an O(n) algorithm.

I believe those learning algorithms here aim to develop long-term in the software industry and are planning to work in programming, so mastering a programming language in depth is very important!

Other Language Versions

Rust

// Version 2, using list (linked list)
use std::collections::LinkedList;
impl Solution{
    pub fn reconstruct_queue(mut people: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let mut queue = LinkedList::new();
        people.sort_by(|a, b| {
            if a[0] == b[0] {
                return a[1].cmp(&b[1]);
            }
            b[0].cmp(&a[0])
        });
        queue.push_back(people[0].clone());
        for v in people.iter().skip(1) {
            if queue.len() > v[1] as usize {
                let mut back_link = queue.split_off(v[1] as usize);
                queue.push_back(v.clone());
                queue.append(&mut back_link);
            } else {
                queue.push_back(v.clone());
            }
        }
        queue.into_iter().collect()
    }
}

Go

In Go, the append operation of a slice is fundamentally similar to the expansion mechanism of a vector in C++.

I say fundamentally because, in practice, the data encountered in everyday coding and work isn’t exceptionally large.

Specifically, when the current length of a slice is less than 1024, performing the append operation will double the capacity of the new slice to the current one; however, when the slice length is 1024 or more, the slice expands by an additional 1/4 of the current slice length each time.

In the underlying implementation of Go Slice, if the capacity is insufficient, a reslice operation is performed, and the underlying array will also be copied anew to another memory region, so appending an element may not always be O(1), it could be O(n)!