53. Maximum Subarray

LeetCode Problem Link (opens new window)

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

• Input: [-2,1,-3,4,-1,2,1,-5,4]
• Output: 6
• Explanation: The subarray [4,-1,2,1] has the largest sum 6.

Approach

Brute Force

The brute force approach involves using a nested loop where the first loop sets the starting position and the second loop traverses the array to find the maximum value.

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT32_MIN;
        int count = 0;
        for (int i = 0; i < nums.size(); i++) { // Set starting position
            count = 0;
            for (int j = i; j < nums.size(); j++) { // Traverse from starting position i to find the maximum value
                count += nums[j];
                result = count > result ? count : result;
            }
        }
        return result;
    }
};

• Time Complexity: O(n^2)
• Space Complexity: O(1)

This brute force solution can barely pass in C++, but may not be feasible in other languages.

Greedy Approach

Where does the greedy part apply?

If -2 and 1 are together, the starting point should definitely be from 1, as negative numbers only decrease the total sum—this is the greedy part of it!

Local optimal: If the current "cumulative sum" becomes negative, immediately abandon it and start recalculating the "cumulative sum" from the next element, because a negative sum will just reduce the overall sum when added to the next element.

Global optimal: Choose the maximum "cumulative sum".

In the case of local optimum, by continually recording the largest "cumulative sum", we can achieve a global optimum.

From a coding perspective: Traverse the nums, start accumulating count from the beginning, and if adding nums[i] results in a negative count, restart the accumulation from nums[i+1] because a negative count will just lower the total sum.

This is equivalent to constantly adjusting the starting position of the maximum subarray in the brute-force solution.

It might be asked: Don't we need to adjust the ending position of the interval to get the maximum "cumulative sum"?

The ending position is actually managed by keeping track of the maximum "cumulative sum" that can be updated in a similar manner, as shown in the following code:

if (count > result) result = count;

Thus, storing the maximum accumulated value acts as a way to adjust the termination position of the subarray.

As shown in the animation below:

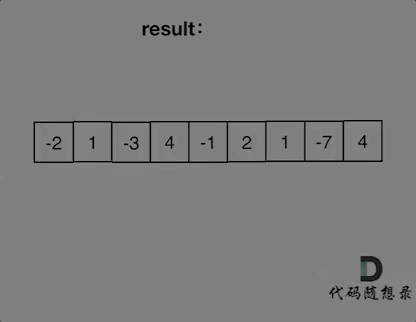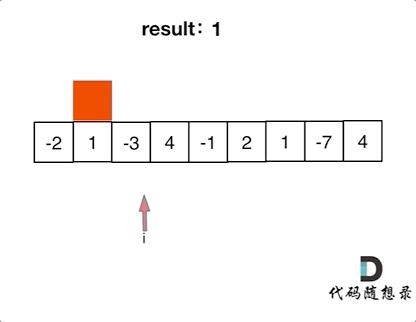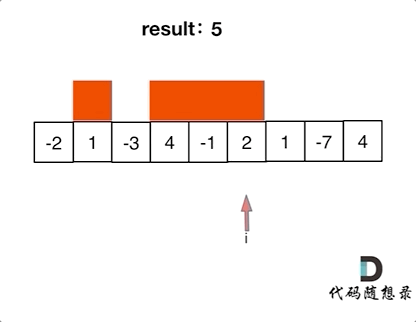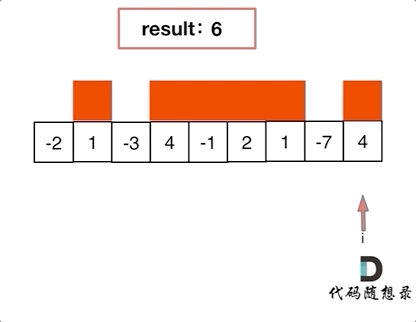
The red starting positions indicate when the greedy algorithm initiates counting when count is positive.

The following C++ code illustrates this (key points are commented):

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int result = INT32_MIN;
        int count = 0;
        for (int i = 0; i < nums.size(); i++) {
            count += nums[i];
            if (count > result) { // Accumulate the maximum value found in the interval (which seems to be equivalent to constantly determining the terminus of the maximum subarray)
                result = count;
            }
            if (count <= 0) count = 0; // Resets the starting point of the maximum subarray as a negative number would only lower the sum
        }
        return result;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(1)

The problem does not specify the expected return value when the array is empty, so any return value can be acceptable in that case.

Common Misconceptions

Misconception 1:

Many believe if the input cases consist entirely of -1, or all negative numbers, this greedy algorithm would result in 0. This is again a classic example of unreliable manual simulation—it's suggested to run the code to see what happens, which also illustrates why result is initialized with the smallest negative number.

Misconception 2:

When using a greedy algorithm to solve this problem, participants often confuse whether the starting point should be chosen when a negative number is encountered or when the continuous sum is negative.

The animation clarifies this: when encountering 4 and then -1, we still accumulate. Why?

Because the sum is still positive even after calculating 4 + -1, which would yield 3, and any positive sum can potentially increase the total sum. Thus, we maintain a positive continuous sum whenever possible.

Some may also worry whether omitting 4 as the maximum continuous sum is a possibility after subtracting -1.

Actually, it's not a concern because another variable, result, is kept to update the maximum continuous sum whenever a larger is found. It thus keeps track of 4, ensuring that intermediate sums like 3 do not affect the final result.

Dynamic Programming

This problem can also be tackled using dynamic programming, which will be detailed in the dynamic programming section of the series. If you're eager to see the dynamic programming approach, you can directly reference here: Dynamic Programming Detailed Version (opens new window)

Here is my dynamic programming code, and those interested can attempt it in advance:

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        vector<int> dp(nums.size(), 0); // dp[i] represents the maximum sum of the subarray including i
        dp[0] = nums[0];
        int result = dp[0];
        for (int i = 1; i < nums.size(); i++) {
            dp[i] = max(dp[i - 1] + nums[i], nums[i]); // State transition formula
            if (dp[i] > result) result = dp[i]; // result keeps track of the maximum value of dp[i]
        }
        return result;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(n)

Conclusion

The greedy idea behind this problem is not easy to come up with, proving that, although the theoretical foundation of greed incurs common sense, greed problems themselves are complex!

Subsequent greedy topics to be introduced are quite challenging, showing just how interesting the greedy algorithm is, so let's not underestimate its complexity!

Other Language Versions

Java

class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 1){
            return nums[0];
        }
        int sum = Integer.MIN_VALUE;
        int count = 0;
        for (int i = 0; i < nums.length; i++){
            count += nums[i];
            sum = Math.max(sum, count); // Accumulate the maximum value found in the interval
            if (count <= 0){
                count = 0; // Resets the starting point of the maximum subarray as a negative number only lowers the sum
            }
        }
       return sum;
    }
}

// DP Method
class Solution {
    public int maxSubArray(int[] nums) {
        int ans = Integer.MIN_VALUE;
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        ans = dp[0];

        for (int i = 1; i < nums.length; i++){
            dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);
            ans = Math.max(dp[i], ans);
        }

        return ans;
    }
}

Python

Brute Force

class Solution:
    def maxSubArray(self, nums):
        result = float('-inf')  # Initialize result to negative infinity
        count = 0
        for i in range(len(nums)):  # Set starting position
            count = 0
            for j in range(i, len(nums)):  # Traverse from starting position i to find the maximum value
                count += nums[j]
                result = max(count, result)  # Update maximum value
        return result

Greedy

class Solution:
    def maxSubArray(self, nums):
        result = float('-inf')  # Initialize result to negative infinity
        count = 0
        for i in range(len(nums)):
            count += nums[i]
            if count > result:  # Accumulate the maximum value found in the interval
                result = count
            if count <= 0:  # Resets the starting point of the maximum subarray as a negative number only lowers the sum
                count = 0
        return result

Dynamic Programming

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        dp = [0] * len(nums)
        dp[0] = nums[0]
        res = nums[0]
        for i in range(1, len(nums)):
            dp[i] = max(dp[i-1] + nums[i], nums[i])
            res = max(res, dp[i])
        return res

Dynamic Programming

class Solution:
    def maxSubArray(self, nums):
        if not nums:
            return 0
        dp = [0] * len(nums)    # dp[i] represents the maximum sum of the subarray including i
        dp[0] = nums[0]
        result = dp[0]
        for i in range(1, len(nums)):
            dp[i] = max(dp[i-1]+nums[i], nums[i])   # State transition formula
            if dp[i] > result:
                result = dp[i]                      # result keeps track of the maximum value of dp[i]
        return result

Optimized Dynamic Programming

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        max_sum = float("-inf") # Initialize result to negative infinity for comparison to obtain maximum value
        current_sum = 0         # Initialize current continuous sum

        for num in nums:

            # Update current continuous sum
            # If adding the current number to the previous continuous sum doesn't surpass the current number, the prior continuous is negative and a fresh calculation is necessary
            current_sum = max(current_sum+num, num) 
            max_sum = max(max_sum, current_sum) # Update result

        return max_sum

Go

Greedy

func maxSubArray(nums []int) int {
    max := nums[0]
    count := 0

    for i := 0; i < len(nums); i++{
        count += nums[i]
        if count > max{
            max = count
        }
        if count < 0 {
            count = 0
        }
    } 
    return max
}

Dynamic Programming

func maxSubArray(nums []int) int {
    maxSum := nums[0]
    for i := 1; i < len(nums); i++ {
        if nums[i] + nums[i-1] > nums[i] {
            nums[i] += nums[i-1]
        }
        if nums[i] > maxSum {
            maxSum = nums[i]
        }
    }
    return maxSum
}

Rust

pub fn max_sub_array(nums: Vec<i32>) -> i32 {
    let mut max_sum = i32::MIN;
    let mut curr = 0;
    for n in nums.iter() {
        curr += n;
        max_sum = max_sum.max(curr);
        curr = curr.max(0);
    }
    max_sum
}

JavaScript:

var maxSubArray = function(nums) {
    let result = -Infinity
    let count = 0
    for(let i = 0; i < nums.length; i++) {
        count += nums[i]
        if(count > result) {
            result = count
        }
        if(count < 0) {
            count = 0
        }
    }
    return result
};

C:

Greedy:

int maxSubArray(int* nums, int numsSize){
    int maxVal = INT_MIN;
    int subArrSum = 0;

    int i;
    for(i = 0; i < numsSize; ++i) {
        subArrSum += nums[i];
        // Update the result if the current local sum is greater than the previous maximum result
        maxVal = subArrSum > maxVal ? subArrSum : maxVal;
        // Reset sub-array calculation when the local sum turns negative
        subArrSum = subArrSum < 0 ? 0 : subArrSum;
    }

    return maxVal;
}

Dynamic Programming:

/**
 * Dynamic programming approach:
 * 1. dp Array: `dp[i]` stores the maximum subarray sum up to i
 * 2. Recurrence Relation: `dp[i] = max(dp[i-1] + nums[i], nums[i])`
    If `dp[i-1]` is negative, it has no benefit for the final result. Thus `dp[i]` takes `nums[i]`.
 * 3. Initialize dp array: `dp[0]` has the maximum subarray sum of `nums[0]`
 * 4. Traverse order: Iterate from the beginning
 */

#define max(a, b) (((a) > (b)) ? (a) : (b))

int maxSubArray(int* nums, int numsSize){
    int dp[numsSize];
    // Maximum subarray sum for `dp[0]` is `nums[0]`
    dp[0] = nums[0];
    // Return `nums[0]` if `numsSize` is 1
    int subArrSum = nums[0];

    int i;
    for(i = 1; i < numsSize; ++i) {
        dp[i] = max(dp[i - 1] + nums[i], nums[i]);

        // If `dp[i]` is greater than previously recorded maximum value, update it
        if(dp[i] > subArrSum)
            subArrSum = dp[i];
    }

    return subArrSum;
}

TypeScript

Greedy

function maxSubArray(nums: number[]): number {
  let curSum: number = 0;
  let resMax: number = -Infinity;
  for (let i = 0, length = nums.length; i < length; i++) {
    curSum += nums[i];
    resMax = Math.max(curSum, resMax);
    if (curSum < 0) curSum = 0;
  }
  return resMax;
}

Dynamic Programming

// Dynamic Programming
function maxSubArray(nums: number[]): number {
  const length = nums.length;
  if (length === 0) return 0;
  const dp: number[] = [];
  dp[0] = nums[0];
  let resMax: number = nums[0];
  for (let i = 1; i < length; i++) {
    dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
    resMax = Math.max(resMax, dp[i]);
  }
  return resMax;
}

Scala

Greedy

object Solution {
  def maxSubArray(nums: Array[Int]): Int = {
    var result = Int.MinValue
    var count = 0
    for (i <- nums.indices) {
      count += nums(i)  // Accumulate count
      if (count > result) result = count  // Record maximum value
      if (count <= 0) count = 0  // Once the count is negative, reset it to zero
    }
    result
  }
}

Dynamic Programming

object Solution {
  def maxSubArray(nums: Array[Int]): Int = {
    var dp = new Array[Int](nums.length)
    var result = nums(0)
    dp(0) = nums(0)
    for (i <- 1 until nums.length) {
      dp(i) = math.max(nums(i), dp(i - 1) + nums(i))
      result = math.max(result, dp(i))  // Update maximum value
    }
    result
  }
}

C#

Greedy

public class Solution
{
    public int MaxSubArray(int[] nums)
    {
        int res = Int32.MinValue;
        int count = 0;
        for (int i = 0; i < nums.Length; i++)
        {
            count += nums[i];
            res = Math.Max(res, count);
            if (count < 0) count = 0;
        }
        return res;
    }
}