56. Merge Intervals

LeetCode Problem Link (opens new window)

Given a collection of intervals, merge all overlapping intervals.

Example 1:

• Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
• Output: [[1,6],[8,10],[15,18]]
• Explanation: Intervals [1,3] and [2,6] overlap, so they are merged into [1,6].

Example 2:

• Input: intervals = [[1,4],[4,5]]
• Output: [[1,5]]
• Explanation: Intervals [1,4] and [4,5] are considered overlapping.

Thought Process

This problem fundamentally is about identifying overlapping intervals.

If you've been following along, you'll notice that this is a similar pattern to problems like 0452. Minimum Number of Arrows to Burst Balloons (opens new window) and 0435. Non-overlapping Intervals (opens new window).

All of these problems involve identifying overlapping intervals, with different logic applied upon finding overlaps. Here, we need to merge overlapping intervals.

The first step is to sort the intervals to ensure they are aligned in a way that makes it easy to identify overlaps, whether by the left boundary or the right. The logic for handling overlaps will differ slightly based on the criteria used.

Once sorted by the left boundary, if intervals[i][0] <= intervals[i - 1][1], it indicates that intervals[i] overlaps with intervals[i - 1]. (Adjacent intervals count as overlapping in this problem, hence the <= comparison.)

Here's an illustrative diagram of how this works: (Note that the intervals in the diagram are already sorted by the left boundary)

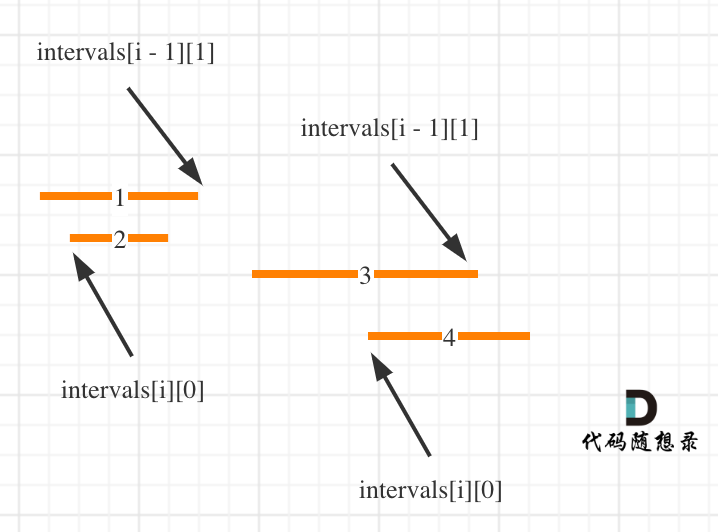
Once we understand how to determine overlaps, we can simulate merging the intervals. Simply update the right boundary of the merged interval and add it to the result array. If there's no merge, add the original interval to the result.

C++ code is as follows:

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> result;
        if (intervals.size() == 0) return result; // Return if the interval collection is empty

        // Using lambda expression for sorting
        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){ return a[0] < b[0]; });

        // The first interval can directly be added to the result set; merge directly on result if overlapping
        result.push_back(intervals[0]);

        for (int i = 1; i < intervals.size(); i++) {
            if (result.back()[1] >= intervals[i][0]) { // Found overlapping interval
                // Merge intervals, just update the right boundary; since we sorted by left boundary, the left is already minimal
                result.back()[1] = max(result.back()[1], intervals[i][1]); 
            } else {
                result.push_back(intervals[i]); // No overlap
            }
        }
        return result;
    }
};

• Time Complexity: O(nlogn)
• Space Complexity: O(logn), due to sorting requirements

Other Language Versions

Java

/**
Time Complexity: O(NlogN) Sorting requires O(NlogN)
Space Complexity: O(logN) Java's built-in sorting uses quick sort, which needs O(logN) space
*/
class Solution {
    public int[][] merge(int[][] intervals) {
        List<int[]> res = new LinkedList<>();
        Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
        // initial start is the smallest left boundary
        int start = intervals[0][0];
        int rightmostRightBound = intervals[0][1];
        for (int i = 1; i < intervals.length; i++) {
            // If the left boundary is greater than the rightmost right boundary
            if (intervals[i][0] > rightmostRightBound) {
                // Add interval and update start
                res.add(new int[]{start, rightmostRightBound});
                start = intervals[i][0];
                rightmostRightBound = intervals[i][1];
            } else {
                // Update rightmost right boundary
                rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
            }
        }
        res.add(new int[]{start, rightmostRightBound});
        return res.toArray(new int[res.size()][]);
    }
}

// Version 2
class Solution {
    public int[][] merge(int[][] intervals) {
        LinkedList<int[]> res = new LinkedList<>();
        Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
        res.add(intervals[0]);
        for (int i = 1; i < intervals.length; i++) {
            if (intervals[i][0] <= res.getLast()[1]) {
                int start = res.getLast()[0];
                int end = Math.max(intervals[i][1], res.getLast()[1]);
                res.removeLast();
                res.add(new int[]{start, end});
            } else {
                res.add(intervals[i]);
            }         
        }
        return res.toArray(new int[res.size()][]);
    }
}

Python

class Solution:
    def merge(self, intervals):
        result = []
        if len(intervals) == 0:
            return result  # Return if the interval collection is empty

        intervals.sort(key=lambda x: x[0])  # Sort by the left boundary of the intervals

        result.append(intervals[0])  # The first interval can directly be added to the result set

        for i in range(1, len(intervals)):
            if result[-1][1] >= intervals[i][0]:  # Found overlapping interval
                # Merge intervals by updating the right boundary, as the sorted order ensures the left boundary is minimal
                result[-1][1] = max(result[-1][1], intervals[i][1])
            else:
                result.append(intervals[i])  # No overlap

        return result

Go

func merge(intervals [][]int) [][]int {
    sort.Slice(intervals, func(i, j int) bool {
        return intervals[i][0] < intervals[j][0]
    })
    res := make([][]int, 0, len(intervals))
    left, right := intervals[0][0], intervals[0][1]
    for i := 1; i < len(intervals); i++ {
        if right < intervals[i][0] {
            res = append(res, []int{left, right})
            left, right = intervals[i][0], intervals[i][1]
        } else {
            right = max(right, intervals[i][1])
        }
    }
    res = append(res, []int{left, right}) // Add the last interval
    return res
}
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

// Version 2
func merge(intervals [][]int) [][]int {
    if len(intervals) == 1 {
        return intervals
    }
    sort.Slice(intervals, func(i, j int) bool {
        return intervals[i][0] < intervals[j][0]
    })
    res := make([][]int, 0)
    res = append(res, intervals[0])
    for i := 1; i < len(intervals); i++ {
        if intervals[i][0] <= res[len(res)-1][1]{
            res[len(res)-1][1] = max56(res[len(res)-1][1],intervals[i][1])
        } else {
            res = append(res, intervals[i])
        }
    }
    return res
}
func max56(a, b int) int {
    if a > b {
        return a
    }
    return b
}

JavaScript

var merge = function (intervals) {
    intervals.sort((a, b) => a[0] - b[0]);
    let prev = intervals[0]
    let result = []
    for(let i =0; i<intervals.length; i++){
        let cur = intervals[i]
        if(cur[0] > prev[1]){
            result.push(prev)
            prev = cur
        }else{
            prev[1] = Math.max(cur[1],prev[1])
        }
    }
    result.push(prev)
    return result
};

Version 2: Left and Right Interval

/**
 * @param {number[][]} intervals
 * @return {number[][]}
 */
var merge = function(intervals) {
    let n = intervals.length;
    if ( n < 2) return intervals;
    intervals.sort((a, b) => a[0]- b[0]);
    let res = [],
        left = intervals[0][0],
        right = intervals[0][1];
    for (let i = 1; i < n; i++) {
        if (intervals[i][0] > right) {
            res.push([left, right]);
            left = intervals[i][0];
            right = intervals[i][1];
        } else {
            right = Math.max(intervals[i][1], right);
        }
    }
    res.push([left, right]);
    return res;
};

TypeScript

function merge(intervals: number[][]): number[][] {
    const resArr: number[][] = [];
    intervals.sort((a, b) => a[0] - b[0]);
    resArr[0] = [...intervals[0]];  // Avoid modifying the original intervals
    for (let i = 1, length = intervals.length; i < length; i++) {
        let interval: number[] = intervals[i];
        let last: number[] = resArr[resArr.length - 1];
        if (interval[0] <= last[1]) {
            last[1] = Math.max(interval[1], last[1]);
        } else {
            resArr.push([...intervals[i]]);
        }
    }
    return resArr;
};

Scala

object Solution {
  import scala.collection.mutable
  def merge(intervals: Array[Array[Int]]): Array[Array[Int]] = {
    var res = mutable.ArrayBuffer[Array[Int]]()

    // Sort
    var interval = intervals.sortWith((a, b) => {
      a(0) < b(0)
    })

    var left = interval(0)(0)
    var right = interval(0)(1)

    for (i <- 1 until interval.length) {
      if (interval(i)(0) <= right) {
        left = math.min(left, interval(i)(0))
        right = math.max(right, interval(i)(1))
      } else {
        res.append(Array[Int](left, right))
        left = interval(i)(0)
        right = interval(i)(1)
      }
    }
    res.append(Array[Int](left, right))
    res.toArray // Return as Array
  }
}

Rust

impl Solution {
    pub fn merge(mut intervals: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let mut res = vec![];
        if intervals.is_empty() {
            return res;
        }
        intervals.sort_by_key(|a| a[0]);
        res.push(intervals[0].clone());
        for interval in intervals.into_iter().skip(1) {
            let res_last_ele = res.last_mut().unwrap();
            if res_last_ele[1] >= interval[0] {
                res_last_ele[1] = interval[1].max(res_last_ele[1]);
            } else {
                res.push(interval);
            }
        }
        res
    }
}

C

#define max(a, b) ((a) > (b) ? (a) : (b))

// Sort by left boundary
int cmp(const void * var1, const void * var2){
    int *v1 = *(int **) var1;
    int *v2 = *(int **) var2;
    return v1[0] - v2[0];
}

int** merge(int** intervals, int intervalsSize, int* intervalsColSize, int* returnSize, int** returnColumnSizes) {
    int ** result = malloc(sizeof (int *) * intervalsSize);
    * returnColumnSizes = malloc(sizeof (int ) * intervalsSize);
    for(int i = 0; i < intervalsSize; i++){
        result[i] = malloc(sizeof (int ) * 2);
    }
    qsort(intervals, intervalsSize, sizeof (int *), cmp);
    int count = 0;
    for(int i = 0; i < intervalsSize; i++){
        // Record left and right boundaries of the interval
        int L = intervals[i][0], R = intervals[i][1];
        // If count is 0 or the previous interval's right is less than the current left, add to result
        if (count == 0 || result[count - 1][1] < L) {
            returnColumnSizes[0][count] = 2;
            result[count][0] = L;
            result[count][1] = R;
            count++;
        } 
        else{ // Update the value of the right boundary
            result[count - 1][1] = max(R, result[count - 1][1]);
        }
    }
    *returnSize = count;
    return result;
}

C#

public class Solution
{
    public int[][] Merge(int[][] intervals)
    {
        if (intervals.Length == 0)
            return intervals;
        Array.Sort(intervals, (a, b) => a[0] - b[0]);
        List<List<int>> res = new List<List<int>>();
        res.Add(intervals[0].ToList());
        for (int i = 1; i < intervals.Length; i++)
        {
            if (res[res.Count - 1][1] >= intervals[i][0])
            {
                res[res.Count - 1][1] = Math.Max(res[res.Count - 1][1], intervals[i][1]);
            }
            else
            {
                res.Add(intervals[i].ToList());
            }
        }
        return res.Select(x => x.ToArray()).ToArray();
    }
}