455. Assign Cookies

LeetCode Problem Link (opens new window)

Assume you are an awesome parent and want to give your children some cookies. But, each child can have at most one cookie.

Each child i has a greed factor g[i], which is the minimum size of a cookie that can satisfy the child; and each cookie j has a size s[j]. If s[j] >= g[i], we can assign the cookie j to the child i, and the child will be satisfied. Your goal is to maximize the number of satisfied children and output this maximum number.

Example 1:

• Input: g = [1,2,3], s = [1,1]
• Output: 1 Explanation: You have three children and two cookies. The greed factors of the three children are 1, 2, 3. Since you have two cookies of size 1, you can only satisfy the child with a greed factor of 1. You should output 1.

Example 2:

• Input: g = [1,2], s = [1,2,3]
• Output: 2
• Explanation: You have two children and three cookies. The greed factors of the two children are 1, 2. You have a sufficient number and size of cookies to fully satisfy both children, so you should output 2.

Constraints:

• 1 <= g.length <= 3 * 10^4
• 0 <= s.length <= 3 * 10^4
• 1 <= g[i], s[j] <= 2^31 - 1

Approach

To satisfy more children, try to avoid wasting cookie sizes.

Large cookies can satisfy both large and small greed factors, so they should be used to satisfy larger greed initially.

The local optimal solution is to feed larger cookies to children with larger greed factors, making full use of the cookie size to satisfy one child. The global optimal solution is to satisfy as many children as possible.

The greedy strategy can be attempted by first sorting the cookie array and the greed factors of the children.

Then iterate through the greed array from back to front and use larger cookies to satisfy greater greed factors, counting the number of children satisfied.

For example:

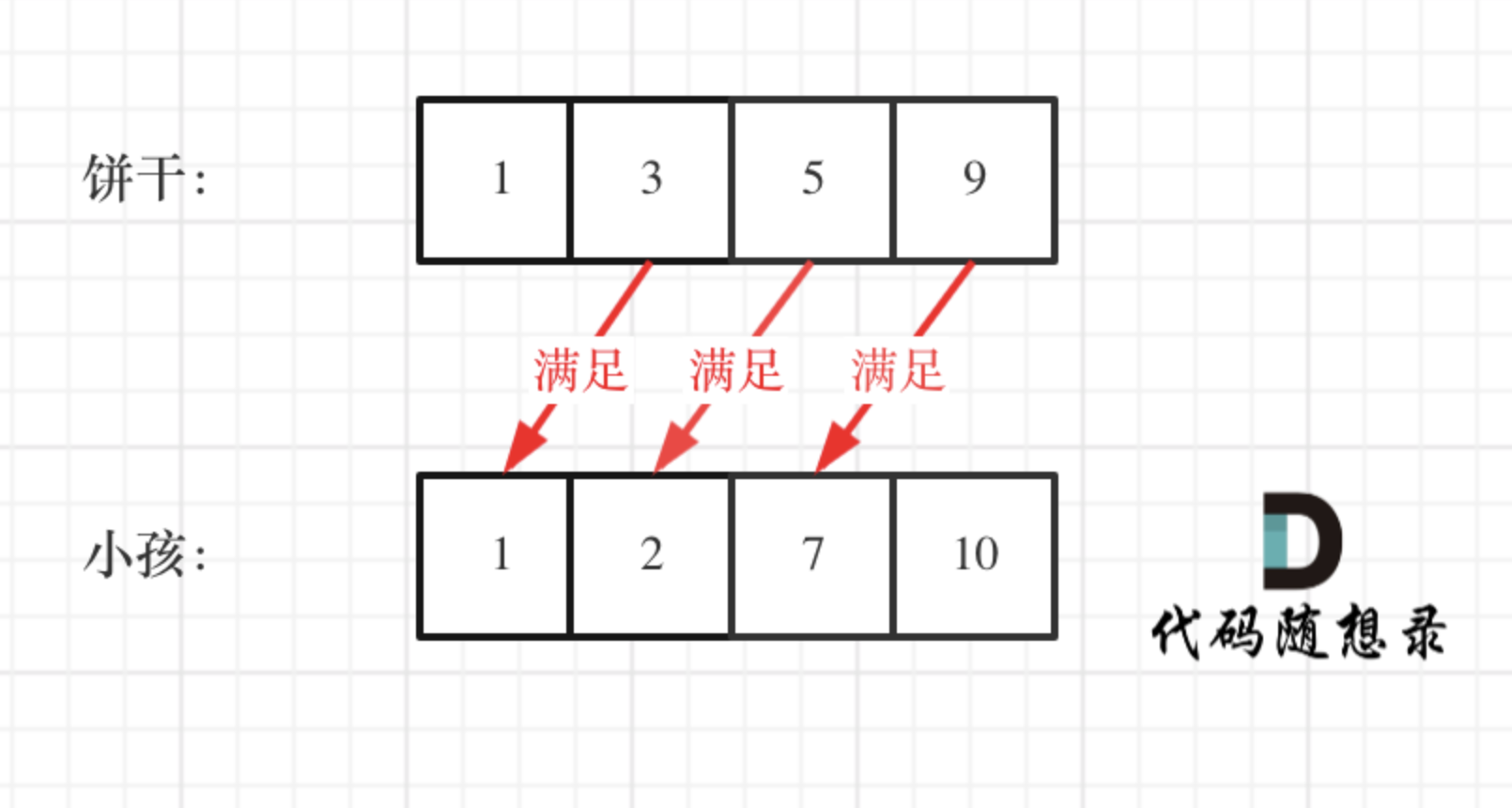
As shown, cookie 9 can only satisfy the child with a greed factor of 7, which is optimal overall. If you can’t think of a counterexample, you can proceed to code.

Overall C++ code below:

// Version 1
class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int index = s.size() - 1; // Index for cookies array
        int result = 0;
        for (int i = g.size() - 1; i >= 0; i--) { // Traverse greed
            if (index >= 0 && s[index] >= g[i]) { // Traverse cookies
                result++;
                index--;
            }
        }
        return result;
    }
};

• Time complexity: O(nlogn)
• Space complexity: O(1)

In the code, you'll notice the use of an index to control the traversal of the cookies array. Instead of another for loop to traverse cookies, decrement is used, which is a common approach.

Some might think of using two for loops for traversing both arrays, but it complicates the logic.

Points to Note

In the first version of the code, you can see that we traverse the greed first, then the cookies. Can we traverse the cookies first, then the greed?

Actually, you cannot.

The outer loop's index i is fixed, while the index in the if condition moves only if the condition is met.

If a for loop controls the cookies and an if loop controls the greed, you would face this scenario:

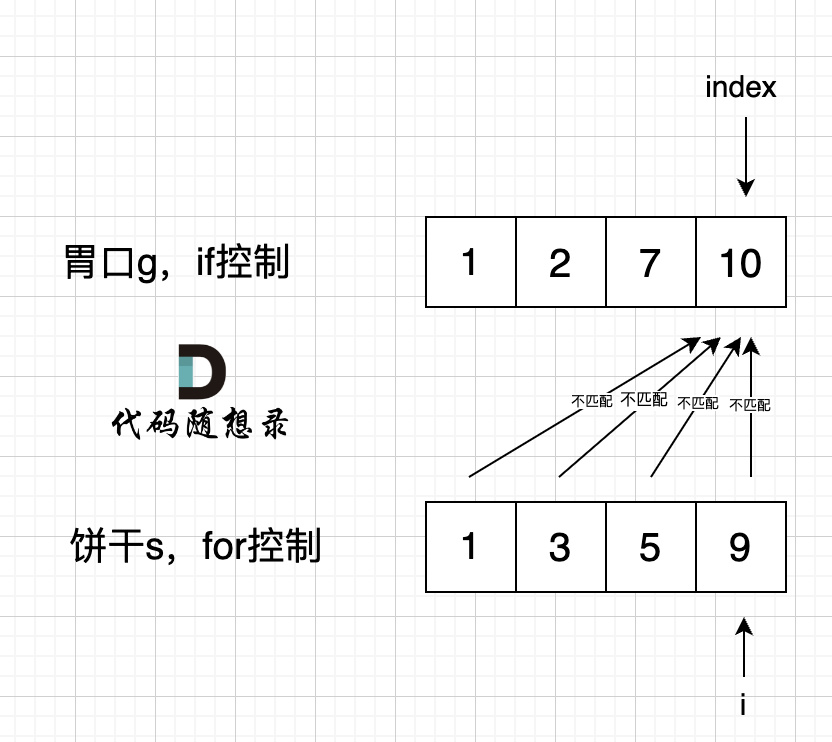
i points to cookie 9 and index to greed 10. Since cookie 9 cannot satisfy greed 10, i will keep advancing, preventing index from moving, which means none of the cookies can be matched.

Therefore, a for loop must control the greed, and an if condition should handle the cookies.

Alternative Approach

An alternative is to use smaller cookies to satisfy smaller greed first

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());
        sort(s.begin(),s.end());
        int index = 0;
        for(int i = 0; i < s.size(); i++) { // Cookies
            if(index < g.size() && g[index] <= s[i]) { // Greed
                index++;
            }
        }
        return index;
    }
};

• Time complexity: O(nlogn)
• Space complexity: O(1)

Observant readers might notice that this writing changes the order of the two loops. First, the cookies are traversed, then the greed, because we traverse from smallest to largest.

Reason already explained in the "Points to Note."

Conclusion

This problem is a good introductory greedy algorithm problem, and the thought process is relatively straightforward.

The article explains the thought process in detail. Think clearly about the local optimal, the global optimal, and whether the local optimal can lead to the global optimal. If no counterexample comes to mind, try a greedy approach.

Other Language Versions

Java

class Solution {
    // Approach 1: Prioritize cookies, small cookies satisfy small greed
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int start = 0;
        int count = 0;
        for (int i = 0; i < s.length && start < g.length; i++) {
            if (s[i] >= g[start]) {
                start++;
                count++;
            }
        }
        return count;
    }
}

class Solution {
    // Approach 2: Prioritize greed, satisfy large greed first
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int count = 0;
        int start = s.length - 1;
        // Traverse greed
        for (int index = g.length - 1; index >= 0; index--) {
            if(start >= 0 && g[index] <= s[start]) {
                start--;
                count++;
            }
        }
        return count;
    }
}

Python

Greedy approach giving large cookies first

class Solution:
    def findContentChildren(self, g, s):
        g.sort()  # Sort the greed factors
        s.sort()  # Sort the cookie sizes
        index = len(s) - 1  # Cookie array index, start from the last cookie
        result = 0  # Number of satisfied children
        for i in range(len(g)-1, -1, -1):  # Traverse greed from last child
            if index >= 0 and s[index] >= g[i]:  # Traverse cookies
                result += 1
                index -= 1
        return result

Greedy approach giving small cookies first

class Solution:
    def findContentChildren(self, g, s):
        g.sort()  # Sort the greed factors
        s.sort()  # Sort the cookie sizes
        index = 0
        for i in range(len(s)):  # Traverse cookies
            if index < len(g) and g[index] <= s[i]:  # If the current child's greed factor is less than or equal to the current cookie size
                index += 1  # Satisfy one child, move to the next child
        return index  # Return the number of satisfied children

Queue approach with large cookies first

from collections import deque
class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        # Approach: Sort cookies and greed from largest to smallest, use deque for queue implementation
        result = 0
        queue_g = deque(sorted(g, reverse=True))
        queue_s = deque(sorted(s, reverse=True))
        while queue_g and queue_s:
            child = queue_g.popleft()
            cookies = queue_s.popleft()
            if child <= cookies:
                result += 1
            else:
                queue_s.appendleft(cookies)
        return result

Go

Version 1 large cookies first

func findContentChildren(g []int, s []int) int {
    sort.Ints(g)
    sort.Ints(s)
    index := len(s) - 1
    result := 0
    for i := len(g) - 1; i >= 0; i-- {
        if index >= 0 && s[index] >= g[i] {
            result++
            index--
        }
    }
    return result
}

Version 2 small cookies first

func findContentChildren(g []int, s []int) int {
    sort.Ints(g)
    sort.Ints(s)
    index := 0
    for i := 0; i < len(s); i++ {
        if index < len(g) && g[index] <= s[i] {
            index++
        }
    }
    return index
}

Rust

pub fn find_content_children(mut children: Vec<i32>, mut cookies: Vec<i32>) -> i32 {
    children.sort();
    cookies.sort();

    let (mut child, mut cookie) = (0, 0);
    while child < children.len() && cookie < cookies.len() {
        // Prioritize the smallest cookie to satisfy the child
        if children[child] <= cookies[cookie] {
            child += 1;
        }
        cookie += 1;
    }
    child as i32
}

JavaScript

var findContentChildren = function (g, s) {
  g = g.sort((a, b) => a - b);
  s = s.sort((a, b) => a - b);
  let result = 0;
  let index = s.length - 1;
  for (let i = g.length - 1; i >= 0; i--) {
    if (index >= 0 && s[index] >= g[i]) {
      result++;
      index--;
    }
  }
  return result;
};

TypeScript

// Large cookies satisfy large greed
function findContentChildren(g: number[], s: number[]): number {
  g.sort((a, b) => a - b);
  s.sort((a, b) => a - b);
  const childLength: number = g.length,
    cookieLength: number = s.length;
  let curChild: number = childLength - 1,
    curCookie: number = cookieLength - 1;
  let resCount: number = 0;
  while (curChild >= 0 && curCookie >= 0) {
    if (g[curChild] <= s[curCookie]) {
      curCookie--;
      resCount++;
    }
    curChild--;
  }
  return resCount;
}

// Small cookies satisfy small greed
function findContentChildren(g: number[], s: number[]): number {
  g.sort((a, b) => a - b);
  s.sort((a, b) => a - b);
  const childLength: number = g.length,
    cookieLength: number = s.length;
  let curChild: number = 0,
    curCookie: number = 0;
  while (curChild < childLength && curCookie < cookieLength) {
    if (g[curChild] <= s[curCookie]) {
      curChild++;
    }
    curCookie++;
  }
  return curChild;
}

C

/// Small cookies satisfy small greed
int cmp(int* a, int* b) {
    return *a - *b;
}

int findContentChildren(int* g, int gSize, int* s, int sSize){
    if(sSize == 0)
        return 0;

    // Sort both arrays in ascending order
    qsort(g, gSize, sizeof(int), cmp);
    qsort(s, sSize, sizeof(int), cmp);

    int numFedChildren = 0;
    int i = 0;
    for(i = 0; i < sSize; ++i) {
        if(numFedChildren < gSize && g[numFedChildren] <= s[i])
            numFedChildren++;
    }
    return numFedChildren;
}

/// Large cookies satisfy large greed
int cmp(int* a, int* b) {
    return *a - *b;
}

int findContentChildren(int* g, int gSize, int* s, int sSize){
    if(sSize == 0)
        return 0;

    // Sort both arrays in ascending order
    qsort(g, gSize, sizeof(int), cmp);
    qsort(s, sSize, sizeof(int), cmp);

    int count = 0;
    int start = sSize - 1;

    for(int i = gSize - 1; i >= 0; i--) {
        if(start >= 0 && s[start] >= g[i] ) {
            start--;
            count++;
        }
    }
    return count;
}

Scala

object Solution {
  def findContentChildren(g: Array[Int], s: Array[Int]): Int = {
    var result = 0
    var children = g.sorted
    var cookie = s.sorted
    // Traverse cookies
    var j = 0
    for (i <- cookie.indices) {
      if (j < children.size && cookie(i) >= children(j)) {
        j += 1
        result += 1
      }
    }
    result
  }
}

C#

public class Solution
{
    public int FindContentChildren(int[] g, int[] s)
    {
        Array.Sort(g);
        Array.Sort(s);
        int index = s.Length - 1;
        int res = 0;
        for (int i = g.Length - 1; i >=0; i--)
        {
            if(index >=0 && s[index]>=g[i])
            {
                res++;
                index--;
            }
        }
        return res;
    }
}