# 135. Candy Distribution
LeetCode Problem Link (opens new window)
A teacher wants to distribute candies to children standing in a line. There are N children, and the teacher gives ratings to each child based on their performance.
You need to help the teacher distribute candies according to the following requirements:
- Each child must receive at least 1 candy.
- Children with a higher rating get more candies than their neighbors.
How many candies does the teacher need to prepare at the minimum?
Example 1:
- Input: [1,0,2]
- Output: 5
- Explanation: You can distribute 2, 1, 2 candies respectively to these three children.
Example 2:
- Input: [1,2,2]
- Output: 4
- Explanation: You can distribute candies as 1, 2, 1 respectively. The third child only gets 1 candy, which already satisfies the conditions.
# Approach
For this problem, you need to consider one direction first, then the other. For example, first compare each child with their left neighbor, then compare with their right. If you consider both directions at once, you might miss some edge cases.
First, determine the case where the child with a higher rating on the right gets more candies (i.e., iterate from left to right).
In this case, the local optimal strategy is: whenever a child on the right has a higher rating than the child on the left, give one more candy to the right child. The global optimal is that children with higher ratings get more candies than their neighbors.
Local optimal can lead to global optimal.
If ratings[i] > ratings[i - 1], then the candies of the ith child must be one more than the i-1th child, so the greedy choice here is: candyVec[i] = candyVec[i - 1] + 1.
Code for the above:
// Iterating from left to right
for (int i = 1; i < ratings.size(); i++) {
if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}
2
3
4
As illustrated:
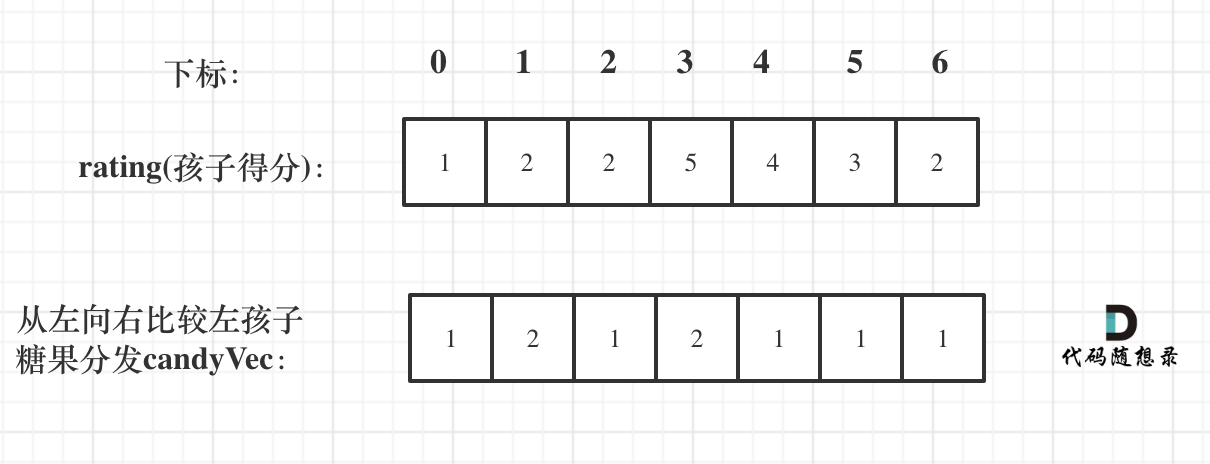
Next, determine the case where the child with a higher rating on the left gets more candies (i.e., iterate from right to left).
Some might wonder why you can't iterate from left to right for this part.
This is because when comparing rating[5] with rating[4], you need to use the comparison result between rating[5] and rating[6], so you must iterate from right to left.
If iterating from left to right, you can't leverage the comparison result between rating[5] and rating[6] when comparing rating[5] and rating[4]. As illustrated:
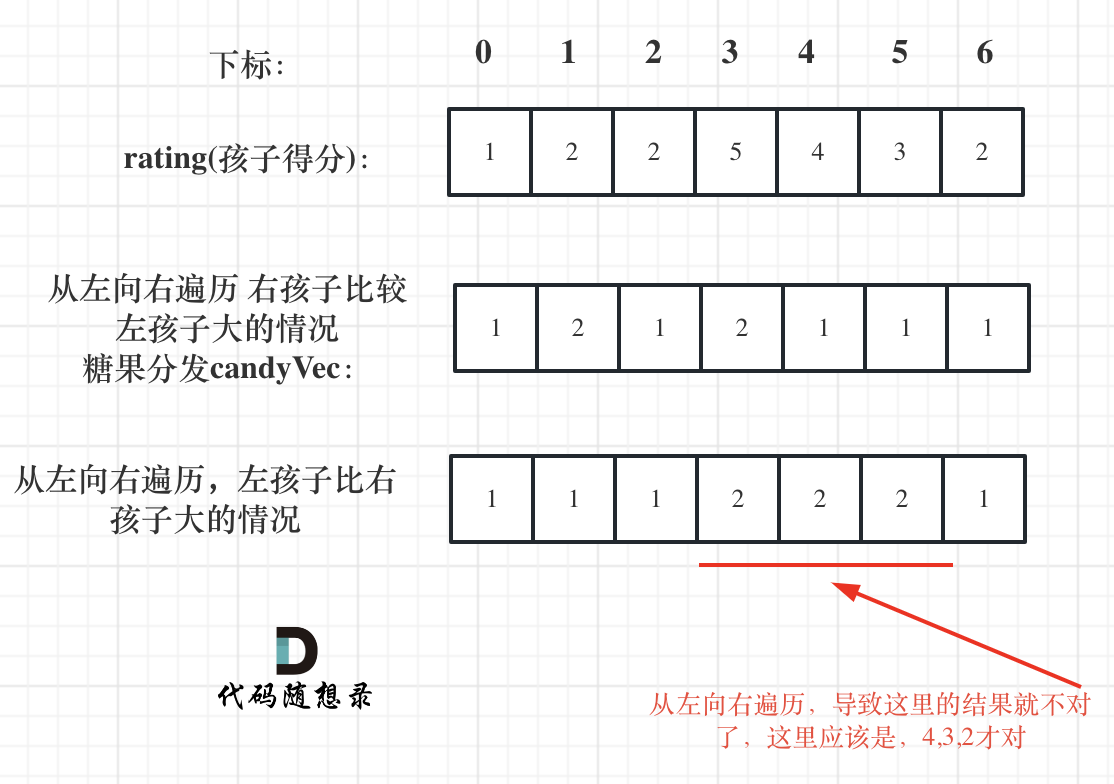
Thus, to determine the situation where the left child has a higher rating than the right child, you must iterate from right to left!
If ratings[i] > ratings[i + 1], then candyVec[i] (the number of candies for the ith child) has two choices: one is candyVec[i + 1] + 1 (derived from adding one candy to the right child), and the other is candyVec[i] (derived from previously considering the case where the right child has a higher rating than the left).
Using a greedy approach again, the local optimal solution is to take the maximum number of candies between candyVec[i + 1] + 1 and candyVec[i], thus ensuring the ith child gets more candies than both its left and right. The global optimal solution is that children with higher ratings get more candies than their neighbors.
Local optimal can lead to global optimal.
Thus, take the maximum candy count between candyVec[i + 1] + 1 and candyVec[i]. Only by taking the maximum can you ensure the ith child's candies exceed both its left and right neighbors'.
As illustrated:
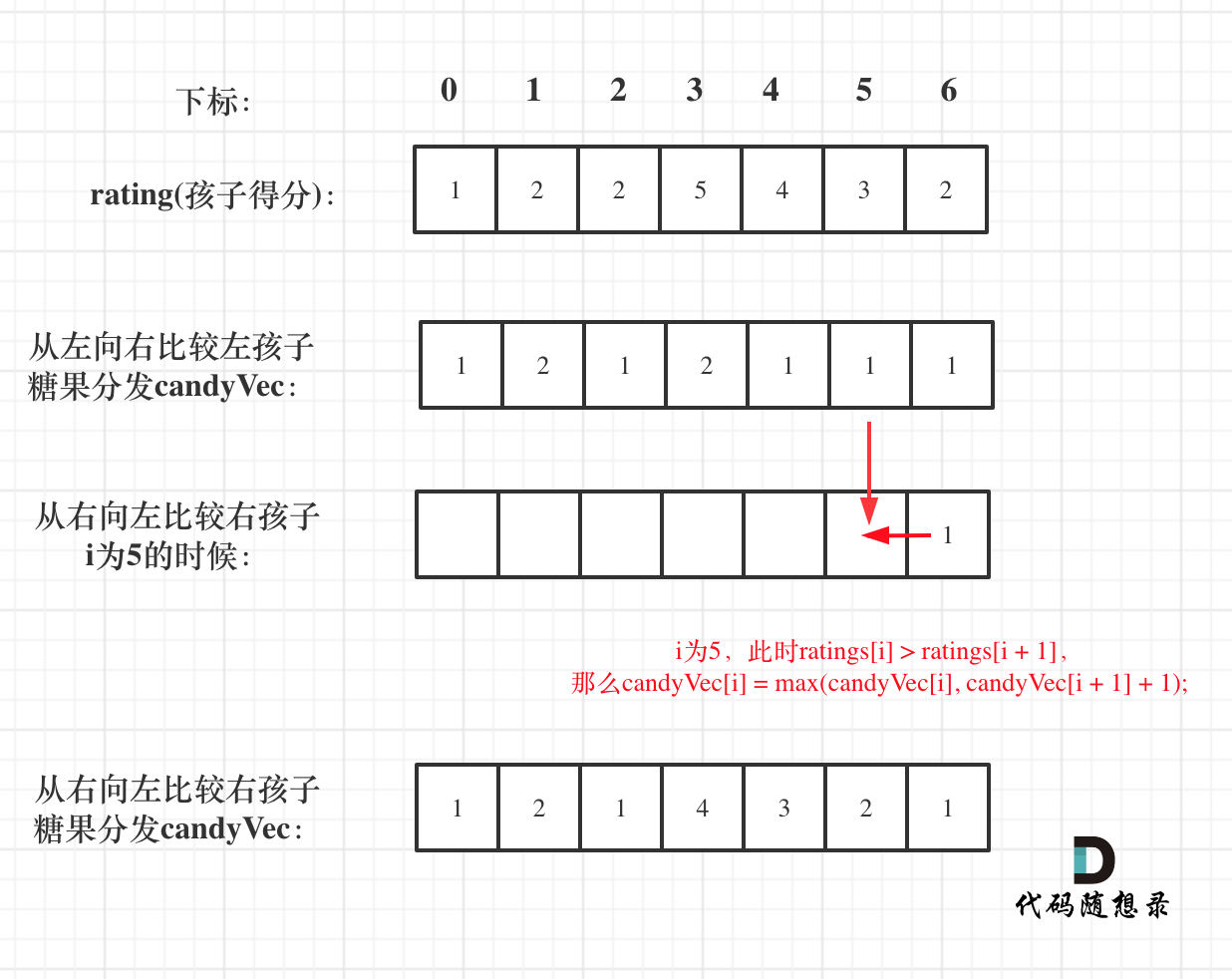
The corresponding code:
// Iterating from right to left
for (int i = ratings.size() - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
}
}
2
3
4
5
6
Complete code:
class Solution {
public:
int candy(vector<int>& ratings) {
vector<int> candyVec(ratings.size(), 1);
// Iterating from left to right
for (int i = 1; i < ratings.size(); i++) {
if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}
// Iterating from right to left
for (int i = ratings.size() - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);
}
}
// Calculate the result
int result = 0;
for (int i = 0; i < candyVec.size(); i++) result += candyVec[i];
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- Time Complexity: O(n)
- Space Complexity: O(n)
# Summary
This is considered a hard problem on LeetCode, and the challenge lies in the greedy strategy. If you try to consider both local aspects simultaneously, you might end up missing some conditions.
Thus, I used two greedy strategies:
- One from left to right, only considering cases where the child's rating on the right is higher than the one on the left.
- Another from right to left, only considering cases where the child's rating on the left is higher than the one on the right.
This method leads to a global optimal solution, where children with higher ratings get more candies than their neighbors.
# Other Language Versions
# Java
class Solution {
/**
* Two phases
* 1. Starting from index 1 left to right, if the right rating is higher than the left, the candy count on the right is the left + 1
* 2. Starting from index ratings.length - 2 right to left, if the left rating is higher than the right, the candy count on the left should be the max of its own count (ensuring it's higher than its left) and the right candy count + 1, ensuring it's higher than both its left and right
*/
public int candy(int[] ratings) {
int len = ratings.length;
int[] candyVec = new int[len];
candyVec[0] = 1;
for (int i = 1; i < len; i++) {
candyVec[i] = (ratings[i] > ratings[i - 1]) ? candyVec[i - 1] + 1 : 1;
}
for (int i = len - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);
}
}
int ans = 0;
for (int num : candyVec) {
ans += num;
}
return ans;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Python
class Solution:
def candy(self, ratings: List[int]) -> int:
n = len(ratings)
candies = [1] * n
# Forward pass: handle cases where right rating is higher than left
for i in range(1, n):
if ratings[i] > ratings[i - 1]:
candies[i] = candies[i - 1] + 1
# Backward pass: handle cases where left rating is higher than right
for i in range(n - 2, -1, -1):
if ratings[i] > ratings[i + 1]:
candies[i] = max(candies[i], candies[i + 1] + 1)
return sum(candies)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Go
func candy(ratings []int) int {
/** first determine one side, then the other
1. Go from left to right, if right is greater than left, add 1
2. Then go from right to left, if left is greater than right, add 1 but make sure it's the minimum required
**/
need := make([]int, len(ratings))
sum := 0
// Initialize (each child gets at least one candy)
for i := 0; i < len(ratings); i++ {
need[i] = 1
}
// 1. Go from left to right, if right is greater than left, add 1
for i := 0; i < len(ratings)-1; i++ {
if ratings[i] < ratings[i+1] {
need[i+1] = need[i] + 1
}
}
// 2. Go from right to left, if left is greater than right, left gets the max of its own count or right + 1
for i := len(ratings)-1; i > 0; i-- {
if ratings[i-1] > ratings[i] {
need[i-1] = findMax(need[i-1], need[i]+1)
}
}
// Sum up total candies
for i := 0; i < len(ratings); i++ {
sum += need[i]
}
return sum
}
func findMax(num1 int, num2 int) int {
if num1 > num2 {
return num1
}
return num2
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# JavaScript
var candy = function(ratings) {
let candys = new Array(ratings.length).fill(1)
for(let i = 1; i < ratings.length; i++) {
if(ratings[i] > ratings[i - 1]) {
candys[i] = candys[i - 1] + 1
}
}
for(let i = ratings.length - 2; i >= 0; i--) {
if(ratings[i] > ratings[i + 1]) {
candys[i] = Math.max(candys[i], candys[i + 1] + 1)
}
}
let count = candys.reduce((a, b) => {
return a + b
})
return count
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Rust
pub fn candy(ratings: Vec<i32>) -> i32 {
let mut candies = vec![1i32; ratings.len()];
for i in 1..ratings.len() {
if ratings[i - 1] < ratings[i] {
candies[i] = candies[i - 1] + 1;
}
}
for i in (0..ratings.len()-1).rev() {
if ratings[i] > ratings[i + 1] {
candies[i] = candies[i].max(candies[i + 1] + 1);
}
}
candies.iter().sum()
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# C
#define max(a, b) (((a) > (b)) ? (a) : (b))
int *initCandyArr(int size) {
int *candyArr = (int*)malloc(sizeof(int) * size);
int i;
for(i = 0; i < size; ++i)
candyArr[i] = 1;
return candyArr;
}
int candy(int* ratings, int ratingsSize){
// Initialize array, each child starts with at least one candy
int *candyArr = initCandyArr(ratingsSize);
int i;
// First determine if the right is rated higher than the left. If yes, right child's candy = left + 1
for(i = 1; i < ratingsSize; ++i) {
if(ratings[i] > ratings[i - 1])
candyArr[i] = candyArr[i - 1] + 1;
}
// Then determine if the left is rated higher than the right. If so, left candy = max of itself or right + 1
for(i = ratingsSize - 1; i > 0; --i) {
if(ratings[i-1] > ratings[i])
candyArr[i-1] = max(candyArr[i-1], candyArr[i]+1);
}
// Sum up total candies
int result = 0;
for(i = 0; i < ratingsSize; ++i) {
result += candyArr[i];
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# TypeScript
function candy(ratings: number[]): number {
const candies: number[] = [];
candies[0] = 1;
// Ensure the higher rated child on right gets more candy than the lower rated one on left
for (let i = 1, length = ratings.length; i < length; i++) {
if (ratings[i] > ratings[i - 1]) {
candies[i] = candies[i - 1] + 1;
} else {
candies[i] = 1;
}
}
// Ensure the higher rated child on left gets more candy than the lower rated one on right
for (let i = ratings.length - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candies[i] = Math.max(candies[i], candies[i + 1] + 1);
}
}
return candies.reduce((pre, cur) => pre + cur);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Scala
object Solution {
def candy(ratings: Array[Int]): Int = {
var candyVec = new Array[Int](ratings.length)
for (i <- candyVec.indices) candyVec(i) = 1
// From left to right
for (i <- 1 until candyVec.length) {
if (ratings(i) > ratings(i - 1)) {
candyVec(i) = candyVec(i - 1) + 1
}
}
// From right to left
for (i <- (candyVec.length - 2) to 0 by -1) {
if (ratings(i) > ratings(i + 1)) {
candyVec(i) = math.max(candyVec(i), candyVec(i + 1) + 1)
}
}
candyVec.sum // Sum up total
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C#
public class Solution
{
public int Candy(int[] ratings)
{
int[] candies = new int[ratings.Length];
for (int i = 0; i < candies.Length; i++)
{
candies[i] = 1;
}
for (int i = 1; i < ratings.Length; i++)
{
if (ratings[i] > ratings[i - 1])
{
candies[i] = candies[i - 1] + 1;
}
}
for (int i = ratings.Length - 2; i >= 0; i--)
{
if (ratings[i] > ratings[i + 1])
{
candies[i] = Math.Max(candies[i], candies[i + 1] + 1);
}
}
return candies.Sum();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
