134. Gas Station

LeetCode Problem Link (opens new window)

There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i + 1). You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return -1.

Note:

• The solution is guaranteed to be unique if it exists.
• Both input arrays are non-empty and have the same length.
• Each element in the input arrays is a non-negative integer.

Example 1:
Input:

• gas = [1,2,3,4,5]
• cost = [3,4,5,1,2]

Output: 3
Explanation:

• Start at station 3, with 4 of gas, then your tank has 0 + 4 = 4 of gas
• Travel to station 4, your tank has 4 - 1 + 5 = 8 of gas
• Travel to station 0, your tank has 8 - 2 + 1 = 7 of gas
• Travel to station 1, your tank has 7 - 3 + 2 = 6 of gas
• Travel to station 2, your tank has 6 - 4 + 3 = 5 of gas
• Travel to station 3, you must consume 5 of gas, which is exactly enough to return to station 3.
• Therefore, 3 is the starting index.

Example 2:
Input:

• gas = [2,3,4]
• cost = [3,4,3]

Output: -1
Explanation: You cannot start at station 0 or 1 as you do not have enough gas to reach the next station. Starting at station 2, you get 4 gas, and your tank has 0 + 4 = 4 gas.
Travel to station 0, your tank has 4 - 3 + 2 = 3 gas.
Travel to station 1, your tank has 3 - 3 + 3 = 3 gas.
You cannot return to station 2 since you'll need 4 of gas, but your tank only has 3.
Thus, it is impossible to travel the circuit in one go no matter how you start.

Thoughts

Brute Force Method

The brute force solution is obviously O(n^2), where we try starting from each gas station and simulate the journey around the circuit.

If after completing the loop, if we have not run out of gas midway, and the final gas in the tank is more than or equal to 0, this starting point is valid.

The brute force method requires simulating the loop, and is not easy to code. The key is simulating the entire circuit.

The for loop is suitable for a linear pass, while the while loop is suitable for a circular traverse, utilize while wisely!

Here's the C++ code:

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        for (int i = 0; i < cost.size(); i++) {
            int rest = gas[i] - cost[i]; // Track remaining gas
            int index = (i + 1) % cost.size();
            while (rest > 0 && index != i) { // Simulate starting at i for one lap (if rest==0, the solution is not unique)
                rest += gas[index] - cost[index];
                index = (index + 1) % cost.size();
            }
            // If starting at i for one lap, gas remaining >=0, return the starting position
            if (rest >= 0 && index == i) return i;
        }
        return -1;
    }
};

• Time Complexity: O(n^2)
• Space Complexity: O(1)

Greedy Algorithm (Method One)

Let's perform greedy selection globally in the following scenarios:

• Case One: If the total gas is less than the total cost, then it's impossible to complete one circuit regardless of where you start.
• Case Two: Track the remaining gas rest[i] = gas[i]-cost[i], accumulate it from the start to the last station. If there is a point where the cumulative sum never drops below zero, point zero can be the starting point.
• Case Three: If the cumulative minimum value is negative, start from a non-zero point, looking backward to find any station that can offset this negative value, and it will be the starting point.

Here's the C++ code:

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int min = INT_MAX; // Track the smallest gas level in the tank from the start
        for (int i = 0; i < gas.size(); i++) {
            int rest = gas[i] - cost[i];
            curSum += rest;
            if (curSum < min) {
                min = curSum;
            }
        }
        if (curSum < 0) return -1;  // Case 1
        if (min >= 0) return 0;     // Case 2
                                    // Case 3
        for (int i = gas.size() - 1; i >= 0; i--) {
            int rest = gas[i] - cost[i];
            min += rest;
            if (min >= 0) {
                return i;
            }
        }
        return -1;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(1)

In my opinion, this is not exactly a greedy algorithm since it doesn't really find a locally optimal solution but rather considers the global optimum directly, though the approach is clever.

Despite this, we call this a greedy algorithm because the solution was derived directly from global optimization. This method is still clever and demonstrates a unique perspective, worth considering.

Greedy Algorithm (Method Two)

Consider another approach: If the total gas minus the total cost is greater than or equal to zero, it is possible to complete a full loop, and the overall remaining gas rest[i] sum is non-negative.

Every gas station's surplus rest[i] is gas[i] - cost[i].

Starting from i=0, accumulate rest[i], with the sum recorded as curSum. As soon as curSum is less than zero, none of [0, i] can be the starting point, because this segment will always run out of gas at i, meaning the starting point must begin after i. Then reset curSum to zero.

Illustration:

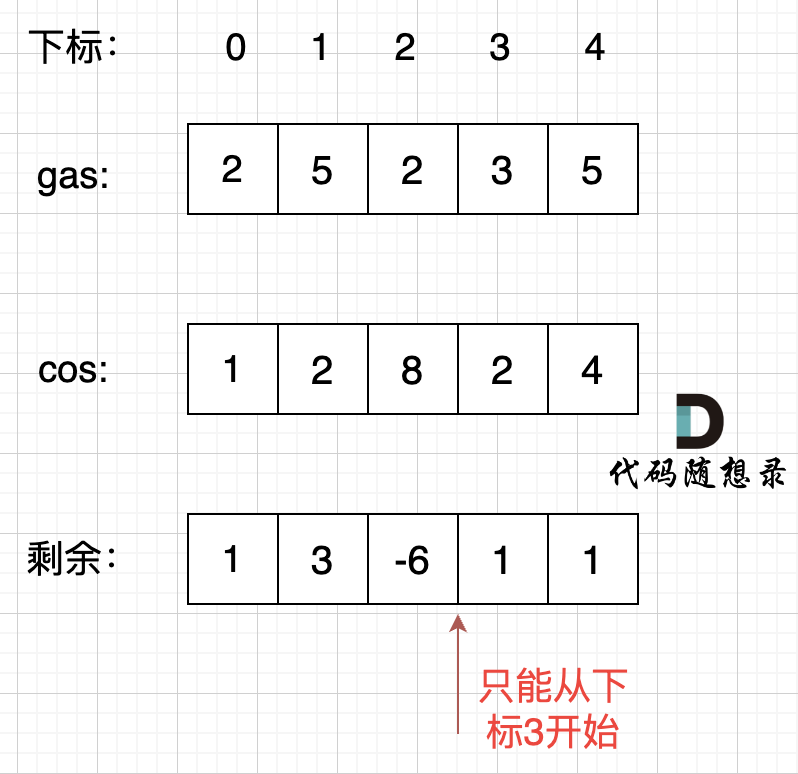
Why is a start point valid if sum from [0 to i] <0 can be simply set to i+1 forward, as curSum will never go lower than it? If it did, more nodes, aka i, would be reset thus repositioning the starting point to i+1 again.

Is it possible for a point in [0, i] to keep curSum non-negative? Higher partition of [0, i] into sections 1, 2, etc. ensuring each section, for example section 2, keeps curSum >=0.

With local optimization: current cumulated rest[i] sum curSum as soon less than 0 signifies start point at least i+1 as starting [0 to i-1] inevitably ran out fuel as per illustration. Global optimization: Find starting point travelling one full circuit.

Local optimum can promote global optimum, let's challenge this with Greedy!

Here's the C++ code:

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int curSum = 0;
        int totalSum = 0;
        int start = 0;
        for (int i = 0; i < gas.size(); i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {   // As soon as current accumulation rest[i] and curSum < 0
                start = i + 1;  // Starting position is updated to i+1
                curSum = 0;     // curSum starts from 0
            }
        }
        if (totalSum < 0) return -1; // Implies it's impossible to complete a circuit
        return start;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(1)

This approach embodies the real greedy algorithm ethos, as the global optimal solution is deduced through local optima, with a clear absence of counter-examples, making it concluded feasible!

Conclusions

Initially proposing a brute force method, the brute force simulation of a loop is quite challenging requiring adept control over while usage.

Followed by two greedy algorithm approaches, the first of which I believe involves direct global optimal simulation, a clever idea, intriguing too.

The second greedy method showcases the essence of greedy strategy, where local optimum is transitionally leading to global optimum solution for selecting a starting position.

Others language versions

Java

// Solution 1
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int sum = 0;
        int min = 0;
        for (int i = 0; i < gas.length; i++) {
            sum += (gas[i] - cost[i]);
            min = Math.min(sum, min);
        }

        if (sum < 0) return -1;
        if (min >= 0) return 0;

        for (int i = gas.length - 1; i > 0; i--) {
            min += (gas[i] - cost[i]);
            if (min >= 0) return i;
        }

        return -1;
    }
}

// Solution 2
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int curSum = 0;
        int totalSum = 0;
        int index = 0;
        for (int i = 0; i < gas.length; i++) {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0) {
                index = (i + 1) % gas.length ; 
                curSum = 0;
            }
        }
        if (totalSum < 0) return -1;
        return index;
    }
}

// Solution 3
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int tank = 0; // current fuel
        int totalGas = 0;  // total gas
        int totalCost = 0; // total cost
        int start = 0; // start point
        for (int i = 0; i < gas.length; i++) {
            totalGas += gas[i];
            totalCost += cost[i];
            
            tank += gas[i] - cost[i];
            if (tank < 0) { // tank becomes negative indicates starting from 0 to i cannot make a full circuit due to fuel shortage
                tank = 0; // reset tank, similar to Problem 53
                start = i + 1; // set start point to i+1
            }
        }
        if (totalCost > totalGas) return -1;
        return start;
    }
}

Python

Brute force

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        for i in range(len(cost)):
            rest = gas[i] - cost[i]  # Track remaining gas
            index = (i + 1) % len(cost)  # Index of the next gas station

            while rest > 0 and index != i:  # Simulate starting at i around one loop (if rest==0, the answer is not unique)
                rest += gas[index] - cost[index]  # Update the remainding gas
                index = (index + 1) % len(cost)  # Update the index of the next gas station

            if rest >= 0 and index == i:  # If starting at i for one lap, remaining gas >=0, and returns to start position
                return i  # Return starting position i

        return -1  # No starting position can loop once, return -1

Greedy (version one)

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        curSum = 0  # Current cumulative remaining fuel
        minFuel = float('inf')  # The smallest amount of fuel in the tank from start
        for i in range(len(gas)):
            rest = gas[i] - cost[i]
            curSum += rest
            if curSum < minFuel:
                minFuel = curSum
        
        if curSum < 0:
            return -1  # Case 1: whole trip's total consumption > total provision, a single loop is impossible
        
        if minFuel >= 0:
            return 0  # Case 2: starting from start, the remaining fuel for all stations does not drop below 0
        
        for i in range(len(gas) - 1, -1, -1):
            rest = gas[i] - cost[i]
            minFuel += rest
            if minFuel >= 0:
                return i  # Case 3: locate station from which starting can ensure fuel is always >=0; return the index
        
        return -1  # Completing a loop isn't possible

Greedy (version two)

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        curSum = 0  # Current cumulative remainder fuel
        totalSum = 0  # Total remaining fuel
        start = 0  # Starting index

        for i in range(len(gas)):
            curSum += gas[i] - cost[i]
            totalSum += gas[i] - cost[i]

            if curSum < 0:  # Current cumulative rest[i] sums per curSum is negative
                start = i + 1  # Starting index updates to i+1
                curSum = 0  # Reset curSum
            
        if totalSum < 0:
            return -1  # Total remaining fuel totalSum < 0, completing a loop is impossible
        return start

Go

Greedy Algorithm (Method One)

func canCompleteCircuit(gas []int, cost []int) int {
    curSum := 0
    min := math.MaxInt64
    for i := 0; i < len(gas); i++ {
        rest := gas[i] - cost[i]
        curSum += rest
        if curSum < min {
            min = curSum
        }
    }
    if curSum < 0 {
        return -1
    }
    if min >= 0 {
        return 0
    }
    for i := len(gas) - 1; i > 0; i-- {
        rest := gas[i] - cost[i]
        min += rest
        if min >= 0 {
            return i
        }
    }
    return -1
}

Greedy Algorithm (Method Two)

func canCompleteCircuit(gas []int, cost []int) int {
	curSum := 0
	totalSum := 0
	start := 0
	for i := 0; i < len(gas); i++ {
		curSum += gas[i] - cost[i]
		totalSum += gas[i] - cost[i]
		if curSum < 0 {
			start = i + 1
			curSum = 0
		}
	}
	if totalSum < 0 {
		return -1
	}
	return start
}

JavaScript

Brute force:

var canCompleteCircuit = function(gas, cost) {
    for(let i = 0; i < cost.length; i++) {
        let rest = gas[i] - cost[i]  // track remaining fuel
        // Walk a full lap starting from i, index is the next station
        let index = (i + 1) % cost.length
        while(rest > 0 && index !== i) {
            rest += gas[index] - cost[index]
            index = (index + 1) % cost.length
        }
        if(rest >= 0 && index === i) return i
    }
    return -1
};

Method One:

var canCompleteCircuit = function(gas, cost) {
    let curSum = 0
    let min = Infinity
    for(let i = 0; i < gas.length; i++) {
        let rest = gas[i] - cost[i]
        curSum += rest
        if(curSum < min) {
            min = curSum
        }
    }
    if(curSum < 0) return -1   //1. Total fuel less than total cost
    if(min >= 0) return 0      //2. Indicates fuel didn't break during travel
                               //3. From rear to fore, look for stations able to offset this negative point, and start from there
    for(let i = gas.length -1; i >= 0; i--) {
        let rest = gas[i] - cost[i]
        min += rest
        if(min >= 0) {
            return i
        }
    }
    return -1
}

Method Two:

var canCompleteCircuit = function(gas, cost) {
    const gasLen = gas.length
    let start = 0
    let curSum = 0
    let totalSum = 0

    for(let i = 0; i < gasLen; i++) {
        curSum += gas[i] - cost[i]
        totalSum += gas[i] - cost[i]
        if(curSum < 0) {
            curSum = 0
            start = i + 1
        }
    }

    if(totalSum < 0) return -1

    return start
};

TypeScript

Brute force:

function canCompleteCircuit(gas: number[], cost: number[]): number {
    for (let i = 0, length = gas.length; i < length; i++) {
        let curSum: number = 0;
        let index: number = i;
        while (curSum >= 0 && index < i + length) {
            let tempIndex: number = index % length;
            curSum += gas[tempIndex] - cost[tempIndex];
            index++;
        }
        if (index === i + length && curSum >= 0) return i;
    }
    return -1;
};

Method Two:

function canCompleteCircuit(gas: number[], cost: number[]): number {
    let total: number = 0;
    let curGas: number = 0;
    let tempDiff: number = 0;
    let resIndex: number = 0;
    for (let i = 0, length = gas.length; i < length; i++) {
        tempDiff = gas[i] - cost[i];
        total += tempDiff;
        curGas += tempDiff;
        if (curGas < 0) {
            resIndex = i + 1;
            curGas = 0;
        }
    }
    if (total < 0) return -1;
    return resIndex;
};

Rust

Greedy Algorithm: Method One

impl Solution {
    pub fn can_complete_circuit(gas: Vec<i32>, cost: Vec<i32>) -> i32 {
        let mut cur_sum = 0;
        let mut min = i32::MAX;
        for i in 0..gas.len() {
            let rest = gas[i] - cost[i];
            cur_sum += rest;
            if cur_sum < min { min = cur_sum; }
        }
        if cur_sum < 0 { return -1; }
        if min > 0 { return 0; }
        for i in (0..gas.len()).rev() {
            let rest = gas[i] - cost[i];
            min += rest;
            if min >= 0 { return i as i32; }
        }
        -1
    }
}

Greedy Algorithm: Method Two

impl Solution {
    pub fn can_complete_circuit(gas: Vec<i32>, cost: Vec<i32>) -> i32 {
        let mut cur_sum = 0;
        let mut total_sum = 0;
        let mut start = 0;
        for i in 0..gas.len() {
            cur_sum += gas[i] - cost[i];
            total_sum += gas[i] - cost[i];
            if cur_sum < 0 {
                start = i + 1;
                cur_sum = 0;
            }
        }
        if total_sum < 0 { return -1; }
        start as i32
    }
}

C

Greedy Algorithm: Method One

int canCompleteCircuit(int* gas, int gasSize, int* cost, int costSize){
    int curSum = 0;
    int i;
    int min = INT_MAX;
    // Traverse the entire array. Calculate the remaining fuel difference at each station, and compare it with minimum cumulative amount.
    for(i = 0; i < gasSize; i++) {
        int diff = gas[i] - cost[i];
        curSum += diff;
        if(curSum < min)
            min = curSum;
    }
    // If the total fuel is negative, it's impossible to complete a full circuit. Return -1
    if(curSum < 0)
        return -1;
    // If min is greater than or equal to 0, every trip's fuel is greater than consumption, allowing departure from zero.
    if(min >= 0)
        return 0;
    // If minimum accumulated is negative, find a non-zero element (fuel exceeds cost) to start. Return the index.
    for(i = gasSize - 1; i >= 0; i--) {
        min+=(gas[i]-cost[i]);
        if(min >= 0)
            return i;
    }
    // Won't logically return this 0
    return 0;
}

Greedy Algorithm: Method Two

int canCompleteCircuit(int* gas, int gasSize, int* cost, int costSize){
    int curSum = 0;
    int totalSum = 0;
    int start = 0;

    int i;
    for(i = 0; i < gasSize; ++i) {
        // The difference between fuel and consumption at the current i station
        int diff = gas[i] - cost[i];

        curSum += diff;
        totalSum += diff;

        // If the gas from 0 to i is negative, start position should be i+1
        if(curSum < 0) {
            curSum = 0;
            // When i + 1 == gasSize, totalSum < 0 (i at gasSize - 1), the car cannot return to the origin
            start = i + 1;
        }
    }

    // If total is less than 0, the fuel car can never return to the origin. Return -1
    if(totalSum < 0)
        return -1;

    return start;
}

Scala

Brute Force:

object Solution {
  def canCompleteCircuit(gas: Array[Int], cost: Array[Int]): Int = {
    for (i <- cost.indices) {
      var rest = gas(i) - cost(i)
      var index = (i + 1) % cost.length // index is the next node of i
      while (rest > 0 && i != index) {
        rest += (gas(index) - cost(index))
        index = (index + 1) % cost.length
      }
      if (rest >= 0 && index == i) return i
    }
    -1
  }
}

Greedy Algorithm: Method One

object Solution {
  def canCompleteCircuit(gas: Array[Int], cost: Array[Int]): Int = {
    var curSum = 0
    var min = Int.MaxValue
    for (i <- gas.indices) {
      var rest = gas(i) - cost(i)
      curSum += rest
      min = math.min(min, curSum)
    }
    if (curSum < 0) return -1 // Case 1: total gas is less than total cost, cannot reach destination
    if (min >= 0) return 0 // Case 2: min >= 0, can start from 0 and reach
    // Case 3: if min is negative, search backwards for a station that fills the minimum
    for (i <- gas.length - 1 to 0 by -1) {
      var rest = gas(i) - cost(i)
      min += rest
      if (min >= 0) return i
    }
    -1
  }
}

Greedy Algorithm: Method Two

object Solution {
  def canCompleteCircuit(gas: Array[Int], cost: Array[Int]): Int = {
    var curSum = 0
    var totalSum = 0
    var start = 0
    for (i <- gas.indices) {
      curSum += (gas(i) - cost(i))
      totalSum += (gas(i) - cost(i))
      if (curSum < 0) {
        start = i + 1 // Update starting point
        curSum = 0  // Reset curSum
      }
    }
    if (totalSum < 0) return -1 // Impossible to go full circle
    start
  }
}

C#

// Greedy Algorithm, Version Two
public class Solution
{
    public int CanCompleteCircuit(int[] gas, int[] cost)
    {
        int curSum = 0, totalSum = 0, start = 0;
        for (int i = 0; i < gas.Length; i++)
        {
            curSum += gas[i] - cost[i];
            totalSum += gas[i] - cost[i];
            if (curSum < 0)
            {
                start = i + 1;
                curSum = 0;
            }
        }
        if (totalSum < 0) return -1;
        return start;
    }
}