763. Partition Labels

LeetCode problem link (opens new window)

String (S) is composed of lowercase letters. We need to partition this string into as many parts as possible so that each letter appears in at most one part. Return a list of integers representing the length of each part.

Example:

• Input: (S = "ababcbacadefegdehijhklij")
• Output: ([9,7,8]) Explanation: The partition is "ababcbaca", "defegde", "hijhklij". Each letter appears in at most one part. A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it contains fewer parts.

Constraints:

• The length of (S) is in [1, 500].
• (S) consists of lowercase letters 'a' to 'z'.

Thought Process

When thinking about string partition, one might first consider a backtracking approach, but this problem doesn’t require brute force backtracking.

The requirement is to put the same letter in the same part as much as possible. How do we ensure all identical letters are encompassed in the same section?

If you haven’t encountered such a problem before, it may seem quite challenging.

While traversing, we want to find the boundary for each letter. If the boundary of all previously traversed letters is reached, then that's a partition point. So, for all letters seen so far, the farthest is up to this boundary.

Break it down into the following steps:

• Record where each character last appears.
• Traverse each character from the beginning and update the farthest position the current character appears. If the farthest position equals the current position, a partition point is found.

As illustrated:

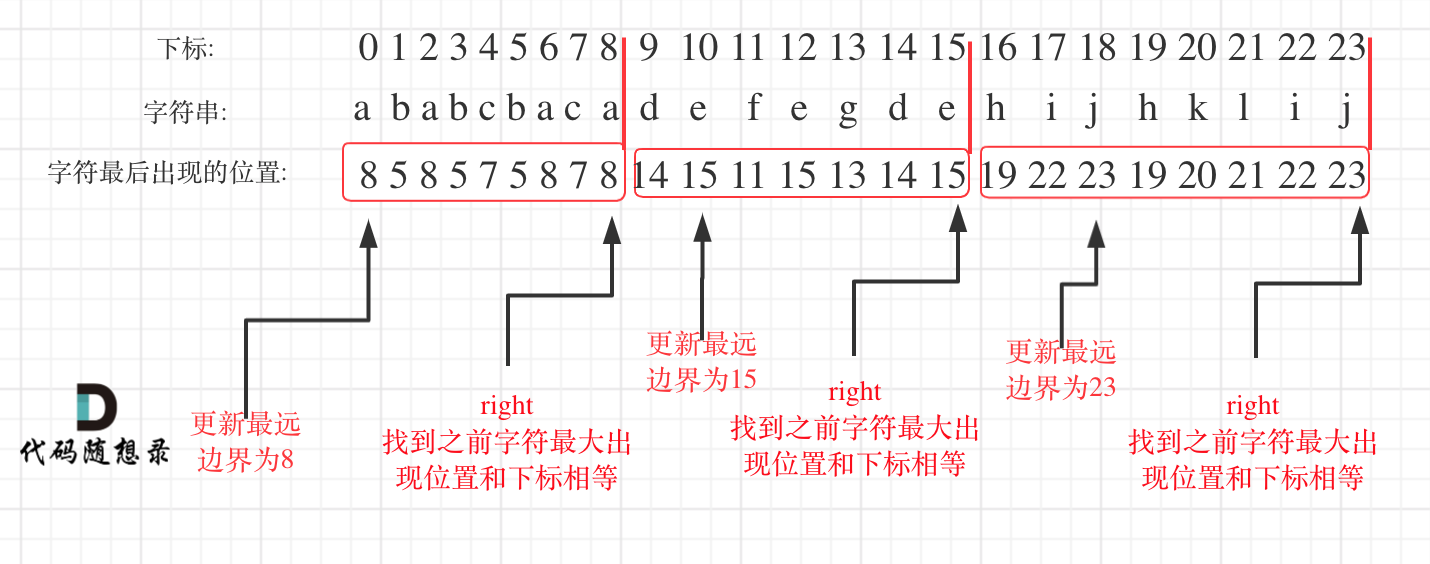
Once understanding the logic, the code is straightforward:

class Solution {
public:
    vector<int> partitionLabels(string S) {
        int hash[27] = {0}; // i represents character, hash[i] is the last position of the character
        for (int i = 0; i < S.size(); i++) { // Record the last position of each character
            hash[S[i] - 'a'] = i;
        }
        vector<int> result;
        int left = 0;
        int right = 0;
        for (int i = 0; i < S.size(); i++) {
            right = max(right, hash[S[i] - 'a']); // Find the farthest boundary for the character
            if (i == right) {
                result.push_back(right - left + 1);
                left = i + 1;
            }
        }
        return result;
    }
};

• Time complexity: (O(n))
• Space complexity: (O(1)), using a fixed-size hash array

Summary

This problem is marked as a greedy algorithm on LeetCode. Honestly, I couldn't feel the greedy aspect, as there isn’t a clear process of deriving global optimality through local optimality. Instead, it simulates enclosing characters' behavior through using farthest appearance distances.

Nevertheless, this approach is clever, introducing value in attempting it.

Supplementary

Here, an approach identical to "0452.Minimum Number of Arrows to Burst Balloons" (opens new window), "0435.Non-overlapping Intervals" (opens new window) is provided.

Count the start and end positions of all characters in the string, recording these intervals (essentially the input format in "0435.Non-overlapping Intervals" (opens new window)). Sort intervals by left boundary from small to large, find boundaries separating groups, which do not overlap. The boundaries found are the answers.

class Solution {
public:
    static bool cmp(vector<int> &a, vector<int> &b) {
        return a[0] < b[0];
    }
    // Record the interval each letter appears in
    vector<vector<int>> countLabels(string s) {
        vector<vector<int>> hash(26, vector<int>(2, INT_MIN));
        vector<vector<int>> hash_filter;
        for (int i = 0; i < s.size(); ++i) {
            if (hash[s[i] - 'a'][0] == INT_MIN) {
                hash[s[i] - 'a'][0] = i;
            }
            hash[s[i] - 'a'][1] = i;
        }
        // Filter out intervals for letters not appearing in the string
        for (int i = 0; i < hash.size(); ++i) {
            if (hash[i][0] != INT_MIN) {
                hash_filter.push_back(hash[i]);
            }
        }
        return hash_filter;
    }
    vector<int> partitionLabels(string s) {
        vector<int> res;
        // This hash is the input format for the non-overlapping intervals problem: list of intervals
        // but here we seek partition points
        vector<vector<int>> hash = countLabels(s);
        // Sort by left boundary from small to large
        sort(hash.begin(), hash.end(), cmp);
        // Record the largest right boundary
        int rightBoard = hash[0][1];
        int leftBoard = 0;
        for (int i = 1; i < hash.size(); ++i) {
            // Since the string can definitely be partitioned,
            // once the left boundary of the next interval is greater than the current right boundary, a partition point is found
            if (hash[i][0] > rightBoard) {
                res.push_back(rightBoard - leftBoard + 1);
                leftBoard = hash[i][0];
            }
            rightBoard = max(rightBoard, hash[i][1]);
        }
        // Rightmost end
        res.push_back(rightBoard - leftBoard + 1);
        return res;
    }
};

Other Language Versions

Java

class Solution {
    public List<Integer> partitionLabels(String S) {
        List<Integer> list = new LinkedList<>();
        int[] edge = new int[26];
        char[] chars = S.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            edge[chars[i] - 'a'] = i;
        }
        int idx = 0;
        int last = -1;
        for (int i = 0; i < chars.length; i++) {
            idx = Math.max(idx, edge[chars[i] - 'a']);
            if (i == idx) {
                list.add(i - last);
                last = i;
            }
        }
        return list;
    }
}

class Solution {
    /* Second solution: Java implementation of the supplementary C++ approach */
    
    public int[][] findPartitions(String s) {
        List<Integer> temp = new ArrayList<>();
        int[][] hash = new int[26][2]; // 26 letters and 2 columns to represent the interval for each letter

        for (int i = 0; i < s.length(); i++) {
            // Update position i for character c
            char c = s.charAt(i);
            if (hash[c - 'a'][0] == 0) hash[c - 'a'][0] = i;

            hash[c - 'a'][1] = i;

            // First element has special handling
            hash[s.charAt(0) - 'a'][0] = 0;
        }

        List<List<Integer>> h = new LinkedList<>();
        // Assemble intervals
        for (int i = 0; i < 26; i++) {
            temp.clear();
            temp.add(hash[i][0]);
            temp.add(hash[i][1]);
            h.add(new ArrayList<>(temp));
        }

        int[][] res = new int[h.size()][2];
        for (int i = 0; i < h.size(); i++) {
            List<Integer> list = h.get(i);
            res[i][0] = list.get(0);
            res[i][1] = list.get(1);
        }

        return res;
    }

    public List<Integer> partitionLabels(String s) {
        int[][] partitions = findPartitions(s);
        List<Integer> res = new ArrayList<>();
        Arrays.sort(partitions, (o1, o2) -> Integer.compare(o1[0], o2[0]));
        int right = partitions[0][1];
        int left = 0;
        for (int i = 0; i < partitions.length; i++) {
            if (partitions[i][0] > right) {
                // A partition occurs when the left boundary exceeds the right boundary
                res.add(right - left + 1);
                left = partitions[i][0];
            }
            right = Math.max(right, partitions[i][1]);
        }
        // Rightmost end
        res.add(right - left + 1);
        return res;
    }
}

Python

Greedy (Version 1)

class Solution:
    def partitionLabels(self, s: str) -> List[int]:
        last_occurrence = {}  # Store the last occurrence of each character
        for i, ch in enumerate(s):
            last_occurrence[ch] = i

        result = []
        start = 0
        end = 0
        for i, ch in enumerate(s):
            end = max(end, last_occurrence[ch])  # Find the farthest occurrence of the current character
            if i == end:  # If the current position is the farthest occurrence, we can partition
                result.append(end - start + 1)
                start = i + 1

        return result

Greedy (Version 2) using the same approach as "0452.Minimum Number of Arrows to Burst Balloons" (opens new window), "0435.Non-overlapping Intervals" (opens new window).

class Solution:
    def countLabels(self, s):
        # Initialize an array of length 26, each with interval [-inf, -inf]
        hash = [[float('-inf'), float('-inf')] for _ in range(26)]
        hash_filter = []
        for i in range(len(s)):
            if hash[ord(s[i]) - ord('a')][0] == float('-inf'):
                hash[ord(s[i]) - ord('a')][0] = i
            hash[ord(s[i]) - ord('a')][1] = i
        for i in range(len(hash)):
            if hash[i][0] != float('-inf'):
                hash_filter.append(hash[i])
        return hash_filter

    def partitionLabels(self, s):
        res = []
        hash = self.countLabels(s)
        hash.sort(key=lambda x: x[0])  # Sort by left boundary from small to large
        rightBoard = hash[0][1]  # Record the maximum right boundary
        leftBoard = 0
        for i in range(1, len(hash)):
            if hash[i][0] > rightBoard:  # A partition point is found
                res.append(rightBoard - leftBoard + 1)
                leftBoard = hash[i][0]
            rightBoard = max(rightBoard, hash[i][1])
        res.append(rightBoard - leftBoard + 1)  # Rightmost end
        return res

Go

func partitionLabels(s string) []int {
    var res []int;
    var marks [26]int;
    size, left, right := len(s), 0, 0;
    for i := 0; i < size; i++ {
        marks[s[i] - 'a'] = i;
    }
    for i := 0; i < size; i++ {
        right = max(right, marks[s[i] - 'a']);
        if i == right {
            res = append(res, right - left + 1);
            left = i + 1;
        }
    }
    return res;
}

func max(a, b int) int {
    if a < b {
        a = b;
    }
    return a;
}

JavaScript

var partitionLabels = function(s) {
    let hash = {}
    for(let i = 0; i < s.length; i++) {
        hash[s[i]] = i
    }
    let result = []
    let left = 0
    let right = 0
    for(let i = 0; i < s.length; i++) {
        right = Math.max(right, hash[s[i]])
        if(right === i) {
            result.push(right - left + 1)
            left = i + 1
        }
    }
    return result
};

TypeScript

function partitionLabels(s: string): number[] {
    const length: number = s.length;
    const resArr: number[] = [];
    const helperMap: Map<string, number> = new Map();
    for (let i = 0; i < length; i++) {
        helperMap.set(s[i], i);
    }
    let left: number = 0;
    let right: number = 0;
    for (let i = 0; i < length; i++) {
        right = Math.max(helperMap.get(s[i])!, right);
        if (i === right) {
            resArr.push(i - left + 1);
            left = i + 1;
        }
    }
    return resArr;
};

Scala

object Solution {
  import scala.collection.mutable
  def partitionLabels(s: String): List[Int] = {
    var hash = new Array[Int](26)
    for (i <- s.indices) {
      hash(s(i) - 'a') = i
    }

    var res = mutable.ListBuffer[Int]()
    var (left, right) = (0, 0)
    for (i <- s.indices) {
      right = math.max(hash(s(i) - 'a'), right)
      if (i == right) {
        res.append(right - left + 1)
        left = i + 1
      }
    }

    res.toList
  }
}

Rust

impl Solution {
    pub fn partition_labels(s: String) -> Vec<i32> {
        let mut hash = vec![0; 26];
        for (i, &c) in s.as_bytes().iter().enumerate() {
            hash[(c - b'a') as usize] = i;
        }
        let mut res = vec![];
        let (mut left, mut right) = (0, 0);
        for (i, &c) in s.as_bytes().iter().enumerate() {
            right = right.max(hash[(c - b'a') as usize]);
            if i == right {
                res.push((right - left + 1) as i32);
                left = i + 1;
            }
        }
        res
    }
}

C

#define max(a, b) ((a) > (b) ? (a) : (b))

int* partitionLabels(char* s, int* returnSize) {
    // Record the last position where each character appears
    int last[26] = {0};
    int len = strlen(s);
    for (int i = 0; i < len; ++i) {
        last[s[i] - 'a'] = i;
    }
    int left = 0, right = 0;
    int * partition = malloc(sizeof (int ) * len);
    // Initialize value
    *returnSize = 0;
    for(int i = 0; i < len; i++){
        right = max(right, last[s[i] - 'a']);
        // If reaching the farthest position, update left index and save result
        if(i == right){
            partition[(*returnSize)++] = right - left + 1;
            left = i + 1;
        }
    }
    return partition;
}

C#

public class Solution
{
    public IList<int> PartitionLabels(string s)
    {
        int[] location = new int[27];
        for (int i = 0; i < s.Length; i++)
        {
            location[s[i] - 'a'] = i;
        }
        List<int> res = new List<int>();
        int left = 0, right = 0;
        for (int i = 0; i < s.Length; i++)
        {
            right = Math.Max(right, location[s[i] - 'a']);
            if (i == right)
            {
                res.Add(right - left + 1);
                left = i + 1;
            }
        }
        return res;
    }
}