# 55. Jump Game
LeetCode Problem Link (opens new window)
You are given a non-negative integer array and you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you can reach the last index.
Example 1:
- Input: [2,3,1,1,4]
- Output: true
- Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Example 2:
- Input: [3,2,1,0,4]
- Output: false
- Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, so you can't reach the last index.
# Approach
When first looking at this problem, you might want to think: If the current element is 3, should I jump 1 step, 2 steps, or 3 steps? Which is the best way to jump?
The number of steps doesn't matter; the key is the range of coverage that you can jump!
You don't need to clearly decide how many steps to jump each time. Just go for the maximum jump length, which is the range you can cover.
Within this range, no matter how you jump, you are guaranteed to be able to jump.
So the problem transforms into checking whether the jump coverage range can reach the endpoint!
Each time you move, take the maximum jumping step (achieve the maximum coverage range). Each time you move one unit forward, update the maximum coverage range.
Greedy algorithm local optimal solution: take the maximum jumping step each time (choose maximum coverage range); overall optimal solution: eventually achieve the overall maximum coverage range to check if it can reach the endpoint.
Local optimum leads to global optimum, and there's no counterexample. Try using a greedy approach!
Illustration:
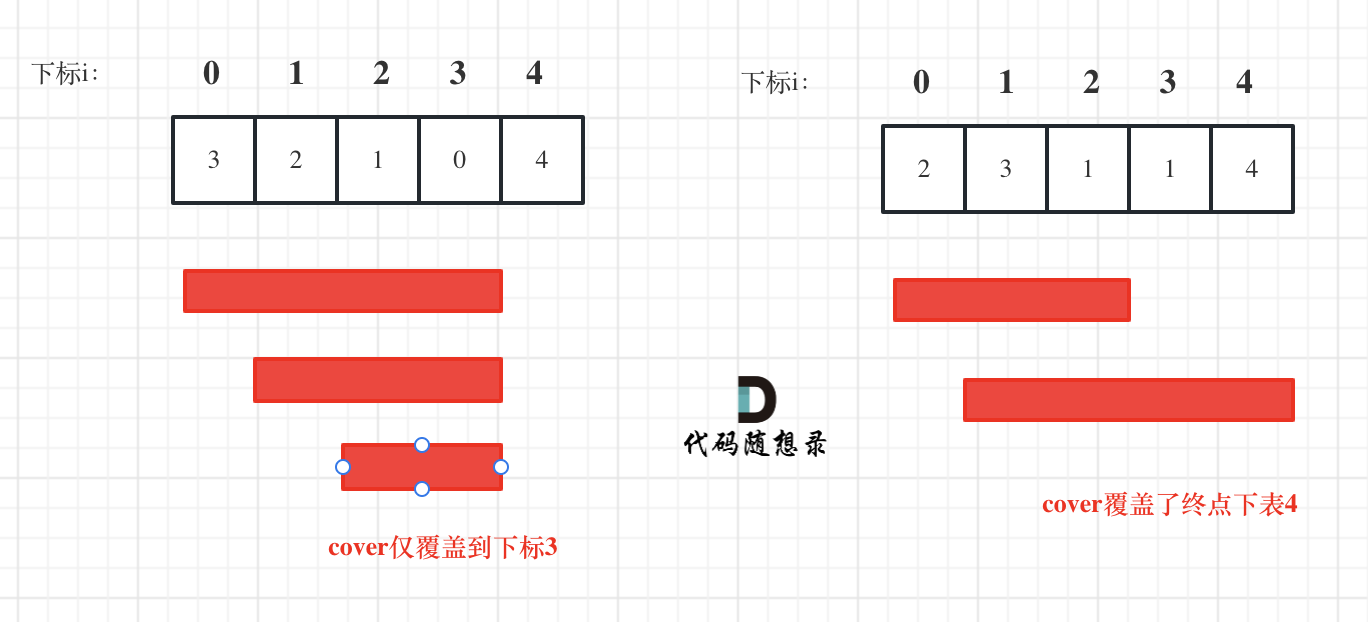
The index i only moves within the range of cover. With each move, the range cover is updated with the value at that index, which supplements the new coverage range, allowing i to continue moving forward.
And cover always takes the maximum between the range supplemented by the current element’s value and the range cover itself.
If cover is greater than or equal to the index of the endpoint, return true.
C++ code is as follows:
class Solution {
public:
bool canJump(vector<int>& nums) {
int cover = 0;
if (nums.size() == 1) return true; // If there's only one element, you can reach the end
for (int i = 0; i <= cover; i++) { // Note that this is less than or equal to cover
cover = max(i + nums[i], cover);
if (cover >= nums.size() - 1) return true; // Indicates that it can cover the endpoint
}
return false;
}
};
2
3
4
5
6
7
8
9
10
11
12
- Time Complexity: O(n)
- Space Complexity: O(1)
# Conclusion
The key to this problem is: Don't be fixated on how many steps should be jumped each time. Instead, pay attention to the coverage range. Within the coverage range, you can definitely jump over, no matter how you jump.
You can see that the thought process is clear, and the code is straightforward once the strategy is figured out.
Some of you might feel that as I explain the greedy series, there's seemingly no connection between different problems?
There's really no clear pattern because greedy algorithms don't have a common formula! There's no overall framework for greedy approaches applicable to solve a series of problems. It’s about being exposed to various types of problems to enhance your understanding of greedy strategies!
# Other Language Versions
# Java
class Solution {
public boolean canJump(int[] nums) {
if (nums.length == 1) {
return true;
}
// Coverage range, initially should be 0 since iteration starts from index 0
int coverRange = 0;
// Update maximum coverage range within the current range
for (int i = 0; i <= coverRange; i++) {
coverRange = Math.max(coverRange, i + nums[i]);
if (coverRange >= nums.length - 1) {
return true;
}
}
return false;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Python
class Solution:
def canJump(self, nums: List[int]) -> bool:
cover = 0
if len(nums) == 1: return True
i = 0
# Python doesn't support dynamically changing variables in `for` loop, using `while` instead
while i <= cover:
cover = max(i + nums[i], cover)
if cover >= len(nums) - 1: return True
i += 1
return False
2
3
4
5
6
7
8
9
10
11
## for loop version
class Solution:
def canJump(self, nums: List[int]) -> bool:
cover = 0
if len(nums) == 1: return True
for i in range(len(nums)):
if i <= cover:
cover = max(i + nums[i], cover)
if cover >= len(nums) - 1: return True
return False
2
3
4
5
6
7
8
9
10
## Based on current farthest reachable position
class Solution:
def canJump(self, nums: List[int]) -> bool:
far = nums[0]
for i in range(len(nums)):
# Consider two situations:
# 1. i <= far - indicates the current position i is reachable
# 2. i > far - indicates the current position i is unreachable
if i > far:
return False
far = max(far, nums[i]+i)
# If the loop ends normally, it indicates the last position is reachable, otherwise it exits prematurely
# Key point is, every position in the list needs to be checked for reachability
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
# Go
// Greedy
func canJump(nums []int) bool {
cover := 0
n := len(nums)-1
for i := 0; i <= cover; i++ { // Each time compare with cover value
cover = max(i+nums[i], cover) // Update cover to the maximum value each step
if cover >= n {
return true
}
}
return false
}
func max(a, b int ) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# JavaScript
var canJump = function(nums) {
if(nums.length === 1) return true
let cover = 0
for(let i = 0; i <= cover; i++) {
cover = Math.max(cover, i + nums[i])
if(cover >= nums.length - 1) {
return true
}
}
return false
};
2
3
4
5
6
7
8
9
10
11
# Rust
impl Solution {
pub fn can_jump(nums: Vec<i32>) -> bool {
if nums.len() == 1 {
return true;
}
let (mut i, mut cover) = (0, 0);
while i <= cover {
cover = (i + nums[i] as usize).max(cover);
if cover >= nums.len() - 1 {
return true;
}
i += 1;
}
false
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# C
#define max(a, b) (((a) > (b)) ? (a) : (b))
bool canJump(int* nums, int numsSize){
int cover = 0;
int i;
// Can only get step counts within cover range, so i <= cover
for(i = 0; i <= cover; ++i) {
// Update cover to the larger value between the value from i and nums[i] and cover itself
cover = max(i + nums[i], cover);
// If updated cover can reach the last element, return true
if(cover >= numsSize - 1)
return true;
}
return false;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# TypeScript
function canJump(nums: number[]): boolean {
let farthestIndex: number = 0;
let cur: number = 0;
while (cur <= farthestIndex) {
farthestIndex = Math.max(farthestIndex, cur + nums[cur]);
if (farthestIndex >= nums.length - 1) return true;
cur++;
}
return false;
}
2
3
4
5
6
7
8
9
10
# Scala
object Solution {
def canJump(nums: Array[Int]): Boolean = {
var cover = 0
if (nums.length == 1) return true // If there's only one element, you can definitely reach it
var i = 0
while (i <= cover) { // i represents the index, it can walk up to cover steps
cover = math.max(i + nums(i), cover)
if (cover >= nums.length - 1) return true // Means can cover the endpoint, return directly
i += 1
}
false // If it doesn't return above, it can't jump there
}
}
2
3
4
5
6
7
8
9
10
11
12
13
# C#
public class Solution
{
public bool CanJump(int[] nums)
{
int cover = 0;
if (nums.Length == 1) return true;
for (int i = 0; i <= cover; i++)
{
cover = Math.Max(i + nums[i], cover);
if (cover >= nums.Length - 1) return true;
}
return false;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
