Compared to Greedy Algorithm: Jump Game (opens new window), this is significantly harder. Be mentally prepared!
# 45. Jump Game II
LeetCode Problem Link (opens new window)
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
Example:
- Input: [2,3,1,1,4]
- Output: 2
- Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.
Note: You can assume that you can always reach the last index.
# Approach
This problem is considerably more difficult compared to 55. Jump Game (opens new window).
However, the thought process is similar, focusing on the maximum coverage range.
To solve this problem with the minimum number of jumps, we need to determine when exactly it is necessary to increase the step count.
A greedy approach would be: locally optimal choice is to move as far as possible; if not at the endpoint, increment steps. Globally optimal choice: take the largest step possible, resulting in the fewest steps.
While the idea is clear, when implementing, we can't just jump as far as possible without considering where the next step can take us.
Thus, when solving, we need to start from the coverage range: no matter how we jump, the coverage range must be reachable, and we want to extend this range with the minimum number of steps. Once the coverage range reaches the endpoint, we have the minimum number of steps!
Two coverage ranges need to be tracked: the maximum range for the current step and for the next step.
If the current position reaches the maximum range for this step and the endpoint is not yet reached, then an additional step is necessary to extend the coverage range until it includes the endpoint.
See the illustration:
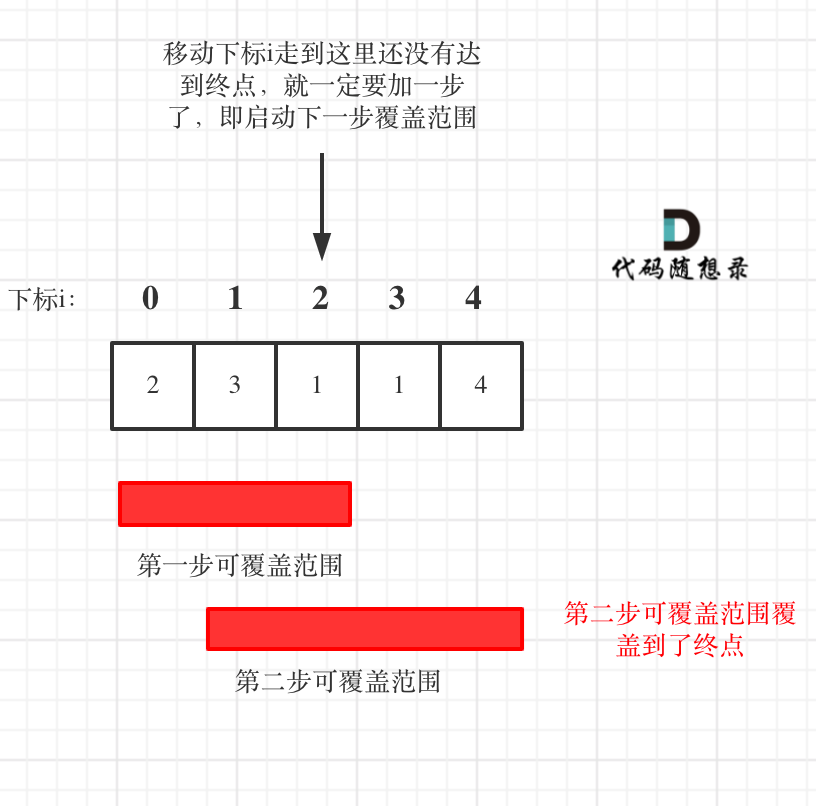
In the illustration, as long as the red area is reached, at most, two more steps are needed!
# Method One
From the illustration, you can see that when the current index reaches the maximum coverage of the current step, the step count should increase to extend the coverage. The final step count will be the minimum number of steps needed.
There's a particular situation to consider: when the index reaches the maximum distance of the current coverage:
- If the index is not the endpoint of the array, step count increases and further steps are needed.
- If the index is the endpoint, no further steps are needed, as you cannot continue.
C++ code is as follows (with detailed comments):
// Version One
class Solution {
public:
int jump(vector<int>& nums) {
if (nums.size() == 1) return 0;
int curDistance = 0; // current maximum coverage index
int ans = 0; // records the maximum number of steps
int nextDistance = 0; // next step maximum coverage index
for (int i = 0; i < nums.size(); i++) {
nextDistance = max(nums[i] + i, nextDistance); // updates the next step maximum coverage index
if (i == curDistance) { // reaches the current maximum coverage index
ans++; // needs to take the next step
curDistance = nextDistance; // updates the current maximum coverage index
if (nextDistance >= nums.size() - 1) break; // the current maximum distance reaches the endpoint, no need to further increment ans, just end
}
}
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
- Time Complexity: O(n)
- Space Complexity: O(1)
# Method Two
This is still a greedy approach, similar to Method One, but the code can be more concise.
For the special case in Method One, handle it uniformly: whenever the current index reaches the current coverage limit, increment the step count without considering whether it is the endpoint.
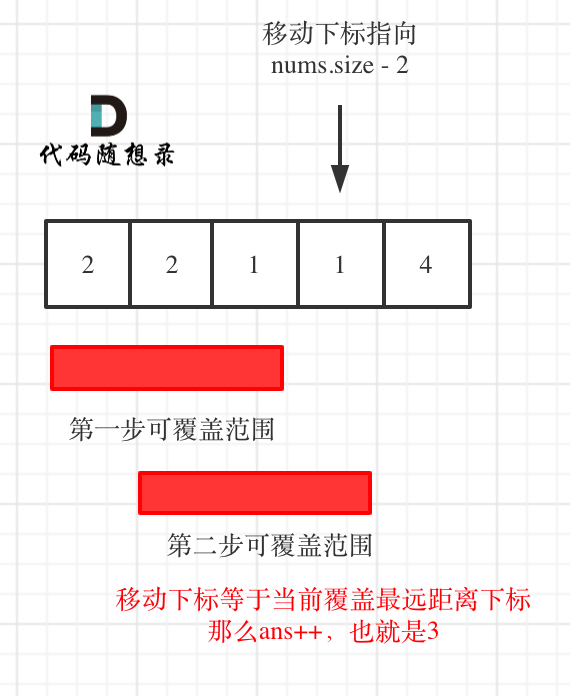
To achieve this, limit the maximum movement of the index to nums.size - 2.
Because when the current index is at nums.size - 2:
If the current index equals the maximum coverage index, it needs to step once more since it can definitely reach the endpoint. (The problem assumes that the last position can always be reached). As shown:
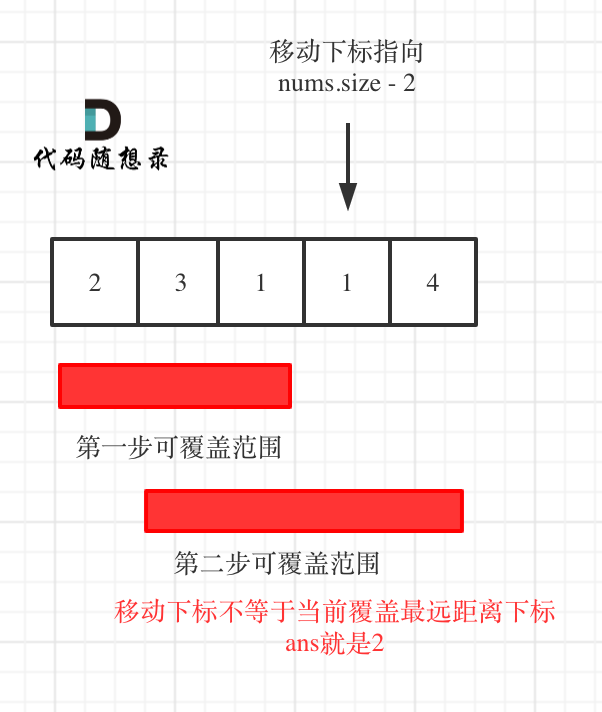
If the current index does not equal the maximum coverage index, then the current coverage can directly reach the end, no further steps are necessary. As shown:
Code is as follows:
// Version Two
class Solution {
public:
int jump(vector<int>& nums) {
int curDistance = 0; // current coverage max index
int ans = 0; // records the max number of steps
int nextDistance = 0; // next step coverage max index
for (int i = 0; i < nums.size() - 1; i++) { // Note that it is less than nums.size() - 1, this is key
nextDistance = max(nums[i] + i, nextDistance); // updates the next step's max coverage index
if (i == curDistance) { // hits current coverage max index
curDistance = nextDistance; // updates current coverage max index
ans++;
}
}
return ans;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: O(n)
- Space Complexity: O(1)
You can see that the code for Version Two simplifies Version One significantly!
The essence lies in controlling the loop index i to only move until nums.size() - 2, so encountering the current max reach index always leads to a step increment without extra considerations.
# Summary
As you can see, this problem is substantially more difficult than 55. Jump Game (opens new window).
While the code itself is quite simple, the greedy approach is ingeniously crafted.
The key to understanding this problem is to extend the maximum coverage with the least steps until it covers the endpoint, ensuring the minimum steps can always reach it without worrying about specific individual leaps.
# Other Language Versions
# Java
// Version One
class Solution {
public int jump(int[] nums) {
if (nums == null || nums.length == 0 || nums.length == 1) {
return 0;
}
// Record jump count
int count=0;
// Current maximum coverage area
int curDistance = 0;
// Maximum coverage area
int maxDistance = 0;
for (int i = 0; i < nums.length; i++) {
// Update maximum coverage area within reachable range
maxDistance = Math.max(maxDistance,i+nums[i]);
// If current step reaches, then another step reaches the end
if (maxDistance>=nums.length-1){
count++;
break;
}
// Upon reaching current max coverage area, update the next possible max area
if (i==curDistance){
curDistance = maxDistance;
count++;
}
}
return count;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// Version Two
class Solution {
public int jump(int[] nums) {
int result = 0;
// Current coverage max index
int end = 0;
// Next step coverage max index
int temp = 0;
for (int i = 0; i <= end && end < nums.length - 1; ++i) {
temp = Math.max(temp, i + nums[i]);
// The number of changes in the reachable position is the number of jumps
if (i == end) {
end = temp;
result++;
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Python
Greedy (Version One)
class Solution:
def jump(self, nums):
if len(nums) == 1:
return 0
cur_distance = 0 # current max coverage index
ans = 0 # record steps
next_distance = 0 # next step max coverage index
for i in range(len(nums)):
next_distance = max(nums[i] + i, next_distance) # update next step max coverage index
if i == cur_distance: # reached current max coverage index
ans += 1 # need next step
cur_distance = next_distance # update current max coverage index
if next_distance >= len(nums) - 1: # current max distance reaches end, no need further increment
break
return ans
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Greedy (Version Two)
class Solution:
def jump(self, nums):
cur_distance = 0 # current max coverage index
ans = 0 # record steps
next_distance = 0 # next step max coverage index
for i in range(len(nums) - 1): # note less than len(nums) - 1, this is key
next_distance = max(nums[i] + i, next_distance) # update next step max coverage index
if i == cur_distance: # reached current max coverage index
cur_distance = next_distance # update current max coverage index
ans += 1
return ans
2
3
4
5
6
7
8
9
10
11
12
13
14
Greedy (Version Three), similar to '55-Jump Game'
class Solution:
def jump(self, nums) -> int:
if len(nums)==1: # if only one element, no jumps needed, steps are 0
return 0
i = 0 # current position
count = 0 # step counter
cover = 0 # current max coverage
while i <= cover: # current position <= current max coverage
for i in range(i, cover+1): # traverse all positions from current to max coverage
cover = max(nums[i]+i, cover) # update current max coverage
if cover >= len(nums)-1: # if current max coverage reaches or exceeds end
return count+1
count += 1 # step count +1 after each round
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Dynamic Programming
class Solution:
def jump(self, nums: List[int]) -> int:
result = [10**4+1] * len(nums) # initialize result array, initial high value
result[0] = 0 # starting position steps are 0
for i in range(len(nums)): # traverse array
for j in range(nums[i] + 1): # traverse range that can jump from current
if i + j < len(nums): # ensure next jump position within array
result[i + j] = min(result[i + j], result[i] + 1) # update min steps for next jump position
return result[-1] # return min steps to reach last position
2
3
4
5
6
7
8
9
10
11
12
# Go
/**
* @date: 2024 Jan 06
* @time: 13:44
* @author: Chris
**/
// Optimized Greedy Algorithm
// Step rule: each crossing of last reachable max range requires a jump, increment step count
// Track position: i == lastDistance + 1
func jump(nums []int) int {
// Per problem rule, start at nums[0]
lastDistance := 0 // previous coverage range
curDistance := 0 // current coverage range (reachable max range)
minStep := 0 // track minimum jump count
for i := 0; i < len(nums); i++ {
if i == lastDistance+1 { // tracking step at position after last reachable range
minStep++ // jump count increment
lastDistance = curDistance // update only at record time
}
curDistance = max(nums[i]+i, curDistance) // update current reachable max range
}
return minStep
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// Greedy Version One
func jump(nums []int) int {
n := len(nums)
if n == 1 {
return 0
}
cur, next := 0, 0
step := 0
for i := 0; i < n; i++ {
next = max(nums[i]+i, next)
if i == cur {
if cur != n-1 {
step++
cur = next
if cur >= n-1 {
return step
}
} else {
return step
}
}
}
return step
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// Greedy Version Two
func jump(nums []int) int {
n := len(nums)
if n == 1 {
return 0
}
cur, next := 0, 0
step := 0
for i := 0; i < n-1; i++ {
next = max(nums[i]+i, next)
if i == cur {
cur = next
step++
}
}
return step
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# JavaScript
var jump = function(nums) {
let curIndex = 0
let nextIndex = 0
let steps = 0
for(let i = 0; i < nums.length - 1; i++) {
nextIndex = Math.max(nums[i] + i, nextIndex)
if(i === curIndex) {
curIndex = nextIndex
steps++
}
}
return steps
};
2
3
4
5
6
7
8
9
10
11
12
13
14
# TypeScript
function jump(nums: number[]): number {
const length: number = nums.length;
let curFarthestIndex: number = 0,
nextFarthestIndex: number = 0;
let curIndex: number = 0;
let stepNum: number = 0;
while (curIndex < length - 1) {
nextFarthestIndex = Math.max(nextFarthestIndex, curIndex + nums[curIndex]);
if (curIndex === curFarthestIndex) {
curFarthestIndex = nextFarthestIndex;
stepNum++;
}
curIndex++;
}
return stepNum;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Scala
object Solution {
def jump(nums: Array[Int]): Int = {
if (nums.length == 0) return 0
var result = 0 // record max steps
var curDistance = 0 // current max coverage index
var nextDistance = 0 // next step max coverage index
for (i <- nums.indices) {
nextDistance = math.max(nums(i) + i, nextDistance) // update next step max coverage index
if (i == curDistance) {
if (curDistance != nums.length - 1) {
result += 1
curDistance = nextDistance
if (nextDistance >= nums.length - 1) return result
} else {
return result
}
}
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Rust
// Version One
impl Solution {
pub fn jump(nums: Vec<i32>) -> i32 {
if nums.len() == 1 {
return 0;
}
let mut cur_distance = 0;
let mut ans = 0;
let mut next_distance = 0;
for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
next_distance = (n as usize + i).max(next_distance);
if i == cur_distance {
if cur_distance < nums.len() - 1 {
ans += 1;
cur_distance = next_distance;
if next_distance >= nums.len() - 1 {
break;
};
} else {
break;
}
}
}
ans
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// Version Two
impl Solution {
pub fn jump(nums: Vec<i32>) -> i32 {
if nums.len() == 1 {
return 0;
}
let mut cur_distance = 0;
let mut ans = 0;
let mut next_distance = 0;
for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
next_distance = (n as usize + i).max(next_distance);
if i == cur_distance {
cur_distance = next_distance;
ans += 1;
}
}
ans
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# C
#define max(a, b) ((a) > (b) ? (a) : (b))
int jump(int* nums, int numsSize) {
if(numsSize == 1){
return 0;
}
int count = 0;
// Current max range that can be reached
int curDistance = 0;
// Next max range that can be reached
int nextDistance = 0;
for(int i = 0; i < numsSize; i++){
nextDistance = max(i + nums[i], nextDistance);
// Index reaches current max distance
if(i == nextDistance){
count++;
curDistance = nextDistance;
}
}
return count;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C#
// Version Two
public class Solution
{
public int Jump(int[] nums)
{
int cur = 0, next = 0, step = 0;
for (int i = 0; i < nums.Length - 1; i++)
{
next = Math.Max(next, i + nums[i]);
if (i == cur)
{
cur = next;
step++;
}
}
return step;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
