452. Minimum Number of Arrows to Burst Balloons

LeetCode Problem Link (opens new window)

There are many spherical balloons in a 2D space. For each balloon, the provided input is the start and end coordinates of the balloon's diameter in the horizontal direction. Since it's horizontal, the vertical coordinate is not important, so only the start and end x-coordinates are sufficient. The start coordinate is always less than the end coordinate.

An arrow can be shot vertically across the x-axis from different points. If an arrow is shot at point x and a balloon has a diameter with start and end coordinates xstart and xend, where xstart ≤ x ≤ xend, the balloon will be burst. There is no limit on the number of arrows that can be shot. Once an arrow is shot, it can continue forward indefinitely. We want to find the minimum number of arrows required to burst all balloons.

Given an array points where points[i] = [xstart, xend], return the minimum number of arrows needed to burst all balloons.

Example 1:

• Input: points = [[10,16],[2,8],[1,6],[7,12]]
• Output: 2
• Explanation: For this example, x = 6 can burst balloons [2,8] and [1,6], and x = 11 can burst the other two balloons.

Example 2:

• Input: points = [[1,2],[3,4],[5,6],[7,8]]
• Output: 4

Example 3:

• Input: points = [[1,2],[2,3],[3,4],[4,5]]
• Output: 2

Example 4:

• Input: points = [[1,2]]
• Output: 1

Example 5:

• Input: points = [[2,3],[2,3]]
• Output: 1

Constraints:

• 0 <= points.length <= 10^4
• points[i].length == 2
• -2^31 <= xstart < xend <= 2^31 - 1

Thought Process

How can we use the minimum number of arrows?

Intuitively, it seems that shooting the most overlapping balloons together would result in the fewest arrows. Is there a situation where two arrows are fired for three overlapping balloons, leaving one to be shot together with others afterward to minimize usage?

After trying to find a counterexample, it appears that such a situation doesn't exist.

Let's try a greedy approach—local optimization: when balloons overlap, shoot them together to use the fewest arrows. Global optimization: use the fewest arrows to burst all balloons.

Once the algorithm is determined, how do we simulate the process of bursting balloons?

If simulating the real bursting process, you'd remove an element from the array when a balloon is popped. That seems straightforward since the balloon is burst.

Upon further reflection, if you sort the balloons, you can traverse the array from front to back and simply skip the burst balloons without removing them, just by keeping a count of arrows.

The thought process so far suggests a greedy approach, so let's tackle the problem.

To make the balloons overlap as much as possible, the array needs to be sorted.

Should the array be sorted by the start or end position of balloons?

Both work, but the traversal order differs. Here, we opt to sort by the start position.

Given the start position is sorted, traversal should be from the front. Try to overlap them as much as possible.

What happens when we encounter overlapping balloons?

When balloons overlap, one arrow can span the region up to the minimum of the right boundaries.

Take the problem example: [[10,16],[2,8],[1,6],[7,12]], for simplicity, sorted as shown:

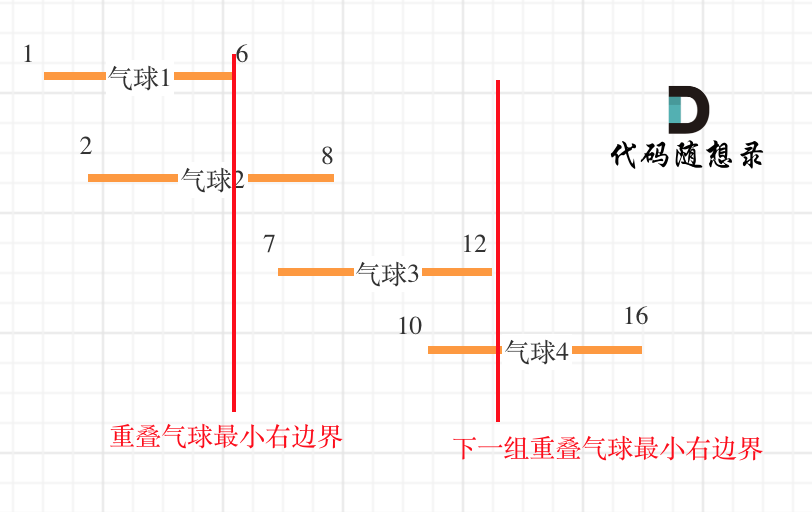
From this, it follows that the first set of overlapping balloons requires an arrow, and as balloon 3’s left boundary surpasses the minimum right boundary of the first group, a second arrow covering balloon 3 is needed.

Here is the C++ code:

class Solution {
private:
    static bool cmp(const vector<int>& a, const vector<int>& b) {
        return a[0] < b[0];
    }
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if (points.size() == 0) return 0;
        sort(points.begin(), points.end(), cmp);

        int result = 1; // At least one arrow is needed when points is not empty
        for (int i = 1; i < points.size(); i++) {
            if (points[i][0] > points[i - 1][1]) {  // Balloons i and i-1 do not overlap, note it's not >=
                result++; // Requires one arrow
            }
            else {  // Balloons i and i-1 overlap
                points[i][1] = min(points[i - 1][1], points[i][1]); // Update the minimum right boundary for overlapping balloons
            }
        }
        return result;
    }
};

• Time Complexity: O(nlog n), due to the sort operation.
• Space Complexity: O(n), given the potential n-level recursive calls in the worst case (reverse order) quicksort, thus requiring O(n) stack space.

The code isn't too complex overall.

Considerations

Note that the problem states: If xstart ≤ x ≤ xend, the balloon will burst. This indicates that if two balloons are adjacent but do not overlap, they can still be burst with one arrow.

Thus, the code if (points[i][0] > points[i - 1][1]) should not use >=

Summary

Although the greedy approach for this problem seems simple and direct—shoot overlapping areas together—it does pose some difficulty.

Even if you've conceived an idea, simulating the balloon bursting process in code might mean actually modeling it by removing elements from the array, potentially complicating matters.

Finding overlapping balloons and their minimum right boundaries involves some nuanced code techniques as well.

Greedy problems can sometimes be straightforward in concept but feel immensely complex when you start writing code.

Building coding expertise requires a lot of practice, seeing, writing, and summarizing.

Code Versions in Other Languages

Java

/**
 * Time Complexity: O(NlogN) for sorting
 * Space Complexity: O(logN) for built-in Java quicksort needing logN space
 */
class Solution {
    public int findMinArrowShots(int[][] points) {
        // Sort by the start of the balloon diameter
        Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));

        int count = 1;  // At least one arrow is needed when points is not empty
        for (int i = 1; i < points.length; i++) {
            if (points[i][0] > points[i - 1][1]) {  // Balloons i and i-1 do not overlap, note it's not >=
                count++; // Needs one arrow
            } else {  // Balloons i and i-1 overlap
                points[i][1] = Math.min(points[i][1], points[i - 1][1]); // Update minimum right boundary for overlapping balloons
            }
        }
        return count;
    }
}

Python

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        if len(points) == 0: return 0
        points.sort(key=lambda x: x[0])
        result = 1
        for i in range(1, len(points)):
            if points[i][0] > points[i - 1][1]: # Balloons i and i-1 do not overlap, note it's not >=
                result += 1     
            else:
                points[i][1] = min(points[i - 1][1], points[i][1]) # Update minimum right boundary for overlapping balloons
        return result

class Solution: # Leaves the original array unchanged
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        if len(points) == 0:
            return 0
            
        points.sort(key=lambda x: x[0])

        # As points is already sorted by the first coordinate, a single variable tracking the right side is needed.
        curr_min_right = points[0][1]
        count = 1
        
        for i in points:
            if i[0] > curr_min_right:
                count += 1
                curr_min_right = i[1]
            else:
                curr_min_right = min(curr_min_right, i[1])
        return count

Go

func findMinArrowShots(points [][]int) int {
    var res int = 1 // Number of arrows
    // Sort by the first coordinate
    sort.Slice(points, func(i, j int) bool {
        return points[i][0] < points[j][0]
    })

    for i := 1; i < len(points); i++ {
        if points[i-1][1] < points[i][0] { // If the right boundary of the previous is less than the left boundary of the current, they surely don't overlap
            res++
        } else {
            points[i][1] = min(points[i-1][1], points[i][1]) // Update minimum right boundary for overlapping balloons
        }
    }
    return res
}
func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

JavaScript

var findMinArrowShots = function(points) {
    points.sort((a, b) => {
        return a[0] - b[0]
    })
    let result = 1
    for(let i = 1; i < points.length; i++) {
        if(points[i][0] > points[i - 1][1]) {
            result++
        } else {
            points[i][1] = Math.min(points[i - 1][1], points[i][1])
        }
    }

    return result
};

TypeScript

function findMinArrowShots(points: number[][]): number {
    const length: number = points.length;
    if (length === 0) return 0;
    points.sort((a, b) => a[0] - b[0]);
    let resCount: number = 1;
    let right: number = points[0][1];   // Right boundary
    let tempPoint: number[];
    for (let i = 1; i < length; i++) {
        tempPoint = points[i];
        if (tempPoint[0] > right) {
            resCount++;
            right = tempPoint[1];
        } else {
            right = Math.min(right, tempPoint[1]);
        }
    }
    return resCount;
};

C

int cmp(const void *a,const void *b)
{
    return ((*((int**)a))[0] > (*((int**)b))[0]);
} 

int findMinArrowShots(int** points, int pointsSize, int* pointsColSize){
    qsort(points, pointsSize, sizeof(points[0]),cmp);
    
    int arrowNum = 1;
    int i = 1;
    for(i = 1; i < pointsSize; i++) {
        if(points[i][0] > points[i-1][1])
            arrowNum++;
        else 
            points[i][1] = points[i][1] > points[i-1][1] ? points[i-1][1] : points[i][1];
    }
    return arrowNum;
}

Rust

impl Solution {
    pub fn find_min_arrow_shots(mut points: Vec<Vec<i32>>) -> i32 {
        if points.is_empty() {
            return 0;
        }
        points.sort_by_key(|point| point[0]);
        let mut result = 1;
        for i in 1..points.len() {
            if points[i][0] > points[i - 1][1] {
                result += 1;
            } else {
                points[i][1] = points[i][1].min(points[i - 1][1])
            }
        }
        result
    }
}

Scala

object Solution {
  def findMinArrowShots(points: Array[Array[Int]]): Int = {
    if (points.length == 0) return 0
    // Sort
    var point = points.sortWith((a, b) => {
      a(0) < b(0)
    })

    var result = 1 // At least one arrow is needed when points is not empty
    for (i <- 1 until point.length) {
      if (point(i)(0) > point(i - 1)(1)) {
        result += 1
      } else {
        point(i)(1) = math.min(point(i - 1)(1), point(i)(1))
      }
    }
    result // Return result
  }
}

C#

public class Solution
{
    public int FindMinArrowShots(int[][] points)
    {
        if (points.Length == 0) return 0;
        Array.Sort(points, (a, b) => a[0].CompareTo(b[0]));
        int count = 1;
        for (int i = 1; i < points.Length; i++)
        {
            if (points[i][0] > points[i - 1][1]) count++;
            else points[i][1] = Math.Min(points[i][1], points[i - 1][1]);
        }
        return count;
    }
}