# 435. Non-overlapping Intervals
LeetCode Problem Link (opens new window)
Given a collection of intervals, find the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Note: You may assume the interval's end is always larger than its start. Intervals like [1,2] and [2,3] are touching but not overlapping.
Example 1:
- Input: [ [1,2], [2,3], [3,4], [1,3] ]
- Output: 1
- Explanation: Remove [1,3] and the rest of the intervals are non-overlapping.
Example 2:
- Input: [ [1,2], [1,2], [1,2] ]
- Output: 2
- Explanation: You need to remove two [1,2] to make the rest of the intervals non-overlapping.
Example 3:
- Input: [ [1,2], [2,3] ]
- Output: 0
- Explanation: You don't need to remove any of the intervals since they're already non-overlapping.
# Approach
Many might instinctively think that sorting is necessary for this problem, but should we sort by the left or the right endpoints?
Actually, both can work. The main goal is to maximize overlap.
I will explain by sorting by the right endpoint and record the number of non-overlapping intervals from left to right. Finally, subtract the number of non-overlapping intervals from the total number of intervals to get the number of intervals that need to be removed.
The problem thus becomes finding the maximum number of non-overlapping intervals.
Recording the number of non-overlapping intervals is a bit tricky, as shown in the image below:
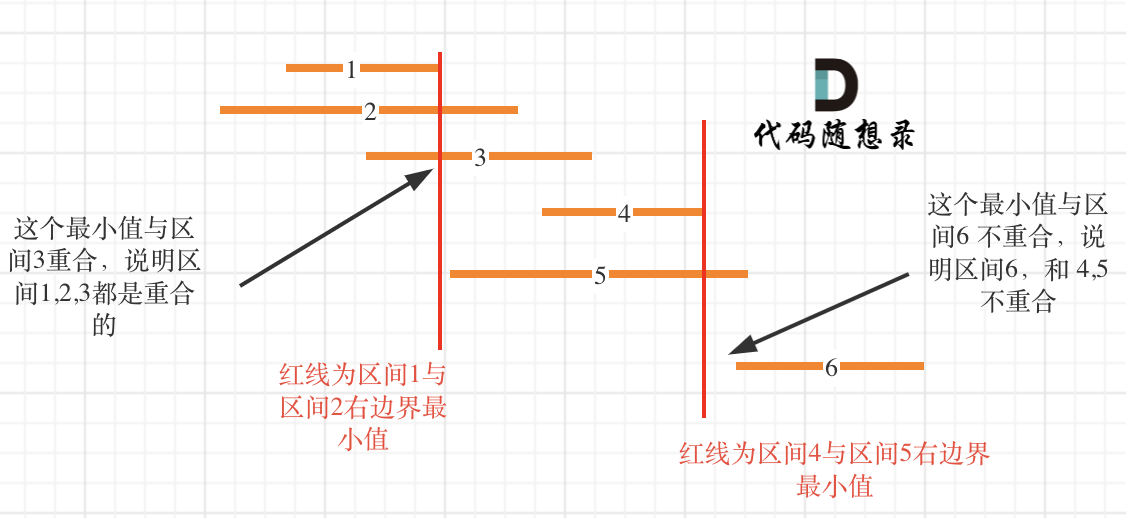
Intervals 1, 2, 3, 4, 5, and 6 are sorted by their right endpoints.
When determining whether intervals 1 and 2 overlap, how do we check overlap with interval 3?
It's by taking the minimum of the right endpoints of intervals 1 and 2, because this minimum value represents the overlapping part of intervals 1 and 2. If this minimum touches interval 3, then intervals 1, 2, and 3 are overlapping.
Next, find the interval that starts after interval 1 ends, starting with interval 4. Some might ask why not start with interval 5? Do not forget we already sorted by the right endpoint.
After completing interval 4, identify interval 6, so in total, the count of non-overlapping intervals is three.
There are 6 intervals in total, subtract the count of non-overlapping intervals (3), and we need to remove 3 intervals.
Here is the C++ code:
class Solution {
public:
// Sort by the right endpoint of the intervals
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[1] < b[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 1; // Records the count of non-overlapping intervals
int end = intervals[0][1]; // Records the division point of the interval
for (int i = 1; i < intervals.size(); i++) {
if (end <= intervals[i][0]) {
end = intervals[i][1];
count++;
}
}
return intervals.size() - count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
- Time complexity: O(nlog n), due to sorting
- Space complexity: O(n), due to sorting, requires n recursive calls in the worst case (reverse sorted order), so indeed requires O(n) stack space
You may notice that such a complex problem has such a simple code implementation!
# Additional Details
# Addition (1)
Is it possible to sort by the left endpoint?
Yes, it is. When sorting by the left endpoint, we are directly counting the overlapping intervals; count records the number of overlaps.
class Solution {
public:
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[0] < b[0]; // Sort by the left endpoint
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 0; // Start from 0, as we are counting overlaps
int end = intervals[0][1]; // Records the division point of the interval
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= end) end = intervals[i][1]; // Non-overlapping case
else { // Overlapping case
end = min(end, intervals[i][1]);
count++;
}
}
return count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
The code can be further streamlined by directly replacing the end variable with intervals[i][1] and simply checking for the overlapping case.
class Solution {
public:
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[0] < b[0]; // Sort by the left endpoint
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int count = 0; // Start from 0, as we are counting overlaps
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] < intervals[i - 1][1]) { // Overlapping case
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]);
count++;
}
}
return count;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Addition (2)
This problem is very similar to 0452.Minimum Number of Arrows to Burst Balloons (opens new window). The number of arrows is analogous to the number of non-overlapping intervals. By slightly modifying the condition for bursting balloons in that problem (by adding an equals sign, which considers [0,1] [1,2] as adjacent intervals), and subtracting the arrow count from the total number of intervals, we obtain the number of intervals needing removal.
By slightly modifying the code from 0452.Minimum Number of Arrows to Burst Balloons (opens new window), we can solve this problem.
class Solution {
public:
// Sort by the right endpoint of the intervals
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[1] < b[1]; // Sort by the right endpoint
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int result = 1; // At least one arrow is needed since points are not empty
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= intervals[i - 1][1]) {
result++; // An arrow is needed
}
else { // Balloon i and balloon i-1 overlap
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // Update the minimum right boundary of the overlapping balloon
}
}
return intervals.size() - result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Here, sorting by the left endpoint or sort by the right endpoint both work and can solve the problem.
class Solution {
public:
// Sort by the left endpoint of the intervals
static bool cmp (const vector<int>& a, const vector<int>& b) {
return a[0] < b[0]; // Sort by the left endpoint
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
int result = 1; // At least one arrow is needed since points are not empty
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= intervals[i - 1][1]) {
result++; // An arrow is needed
}
else { // Balloon i and balloon i-1 overlap
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]); // Update the minimum right boundary of the overlapping balloon
}
}
return intervals.size() - result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Other Language Versions
# Java
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> {
return Integer.compare(a[0],b[0]);
});
int count = 1;
for(int i = 1; i < intervals.length; i++){
if(intervals[i][0] < intervals[i - 1][1]){
intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);
continue;
} else {
count++;
}
}
return intervals.length - count;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
When sorted by the left endpoint, regardless of the order of the right, we handle overlapping by taking the smaller of the right endpoints.
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> {
return Integer.compare(a[0],b[0]);
});
int remove = 0;
int pre = intervals[0][1];
for(int i = 1; i < intervals.length; i++) {
if(pre > intervals[i][0]) {
remove++;
pre = Math.min(pre, intervals[i][1]);
}
else pre = intervals[i][1];
}
return remove;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Python
Greedy approach based on the left endpoint
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if not intervals:
return 0
intervals.sort(key=lambda x: x[0]) # Sort by the left endpoint in ascending order
count = 0 # Record the number of overlapping intervals
for i in range(1, len(intervals)):
if intervals[i][0] < intervals[i - 1][1]: # Overlapping intervals exist
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]) # Update the right endpoint of the overlapping interval
count += 1
return count
2
3
4
5
6
7
8
9
10
11
12
13
14
Greedy approach based on the left endpoint by modifying the code from 452.Minimum Number of Arrows to Burst Balloons (opens new window)
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
if not intervals:
return 0
intervals.sort(key=lambda x: x[0]) # Sort by the left endpoint in ascending order
result = 1 # The number of non-overlapping intervals, initialized to 1, as there is at least one non-overlapping interval
for i in range(1, len(intervals)):
if intervals[i][0] >= intervals[i - 1][1]: # No overlapping
result += 1
else: # Overlapping case
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1]) # Update the right endpoint of the overlapping interval
return len(intervals) - result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Go
func eraseOverlapIntervals(intervals [][]int) int {
sort.Slice(intervals, func(i, j int) bool {
return intervals[i][1] < intervals[j][1]
})
res := 1
for i := 1; i < len(intervals); i++ {
if intervals[i][0] >= intervals[i-1][1] {
res++
} else {
intervals[i][1] = min(intervals[i - 1][1], intervals[i][1])
}
}
return len(intervals) - res
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# JavaScript
- Sort by the right endpoint
var eraseOverlapIntervals = function(intervals) {
intervals.sort((a, b) => {
return a[1] - b[1]
})
let count = 1
let end = intervals[0][1]
for(let i = 1; i < intervals.length; i++) {
let interval = intervals[i]
if(interval[0] >= end) {
end = interval[1]
count += 1
}
}
return intervals.length - count
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- Sort by the left endpoint
var eraseOverlapIntervals = function(intervals) {
// Sort by the left endpoint in ascending order
intervals.sort((a, b) => a[0] - b[0])
let count = 1
let end = intervals[intervals.length - 1][0]
// Traverse in reverse order, as for individual intervals, the larger the left endpoint, the greater the space for the previous interval
for(let i = intervals.length - 2; i >= 0; i--) {
if(intervals[i][1] <= end) {
count++
end = intervals[i][0]
}
}
// Count records the maximum number of non-overlapping intervals
return intervals.length - count
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# TypeScript
Sort by the right endpoint and iterate from left to right
function eraseOverlapIntervals(intervals: number[][]): number {
const length = intervals.length;
if (length === 0) return 0;
intervals.sort((a, b) => a[1] - b[1]);
let right: number = intervals[0][1];
let count: number = 1;
for (let i = 1; i < length; i++) {
if (intervals[i][0] >= right) {
count++;
right = intervals[i][1];
}
}
return length - count;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Sort by the left endpoint and iterate from left to right
function eraseOverlapIntervals(intervals: number[][]): number {
if (intervals.length === 0) return 0;
intervals.sort((a, b) => a[0] - b[0]);
let right: number = intervals[0][1];
let tempInterval: number[];
let resCount: number = 0;
for (let i = 1, length = intervals.length; i < length; i++) {
tempInterval = intervals[i];
if (tempInterval[0] >= right) {
// Non-overlapping
right = tempInterval[1];
} else {
// Overlapping, remove the one with the larger right boundary from the current interval and the previous interval
right = Math.min(right, tempInterval[1]);
resCount++;
}
}
return resCount;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Scala
object Solution {
def eraseOverlapIntervals(intervals: Array[Array[Int]]): Int = {
var result = 0
var interval = intervals.sortWith((a, b) => {
a(1) < b(1)
})
var edge = Int.MinValue
for (i <- 0 until interval.length) {
if (edge <= interval(i)(0)) {
edge = interval(i)(1)
} else {
result += 1
}
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Rust
impl Solution {
pub fn erase_overlap_intervals(mut intervals: Vec<Vec<i32>>) -> i32 {
if intervals.is_empty() {
return 0;
}
intervals.sort_by_key(|interval| interval[1]);
let mut count = 1;
let mut end = intervals[0][1];
for v in intervals.iter().skip(1) {
if end <= v[0] {
end = v[1];
count += 1;
}
}
(intervals.len() - count) as i32
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# C
// Sort by the right endpoints of the intervals
int cmp(const void * var1, const void * var2){
return (*(int **) var1)[1] - (*(int **) var2)[1];
}
int eraseOverlapIntervals(int** intervals, int intervalsSize, int* intervalsColSize) {
if(intervalsSize == 0){
return 0;
}
qsort(intervals, intervalsSize, sizeof (int *), cmp);
// Records the count of non-overlapping intervals
int count = 1;
// Records the division point of the interval
int end = intervals[0][1];
for(int i = 1; i < intervalsSize; i++){
if(end <= intervals[i][0]){
end = intervals[i][1];
count++;
}
}
return intervalsSize - count;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C#
public class Solution
{
public int EraseOverlapIntervals(int[][] intervals)
{
if (intervals.Length == 0) return 0;
Array.Sort(intervals, (a, b) => a[1].CompareTo(b[1]));
int res = 1, end = intervals[0][1];
for (int i = 1; i < intervals.Length; i++)
{
if (end <= intervals[i][0])
{
end = intervals[i][1];
res++;
}
}
return intervals.Length - res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
