# 376. Wiggle Subsequence
LeetCode Problem Link (opens new window)
A sequence of numbers is called a wiggle sequence if the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with fewer than two elements is trivially a wiggle sequence.
For example, [1,7,4,9,2,5] is a wiggle sequence because the differences (6,-3,5,-7,3) alternate between positive and negative. In contrast, the sequence [1,4,7,2,5] and [1,7,4,5,5] are not wiggle sequences, the first because its first two differences are positive and the second because its last difference is zero.
Given an integer sequence, return the length of the longest subsequence that is a wiggle sequence. A subsequence is obtained by deleting some elements (or none) from the original sequence, leaving the remaining elements in their original order.
Example 1:
- Input:
[1,7,4,9,2,5] - Output:
6 - Explanation: The entire sequence is a wiggle sequence.
Example 2:
- Input:
[1,17,5,10,13,15,10,5,16,8] - Output:
7 - Explanation: There are several subsequences that qualify as wiggle sequences, such as
[1,17,10,13,10,16,8].
Example 3:
- Input:
[1,2,3,4,5,6,7,8,9] - Output:
2
# Approach
# Approach 1 (Greedy Algorithm)
This problem requires obtaining the longest subsequence that is a wiggle sequence by possibly deleting some elements. The solution principles are:
For Example 2, as shown:
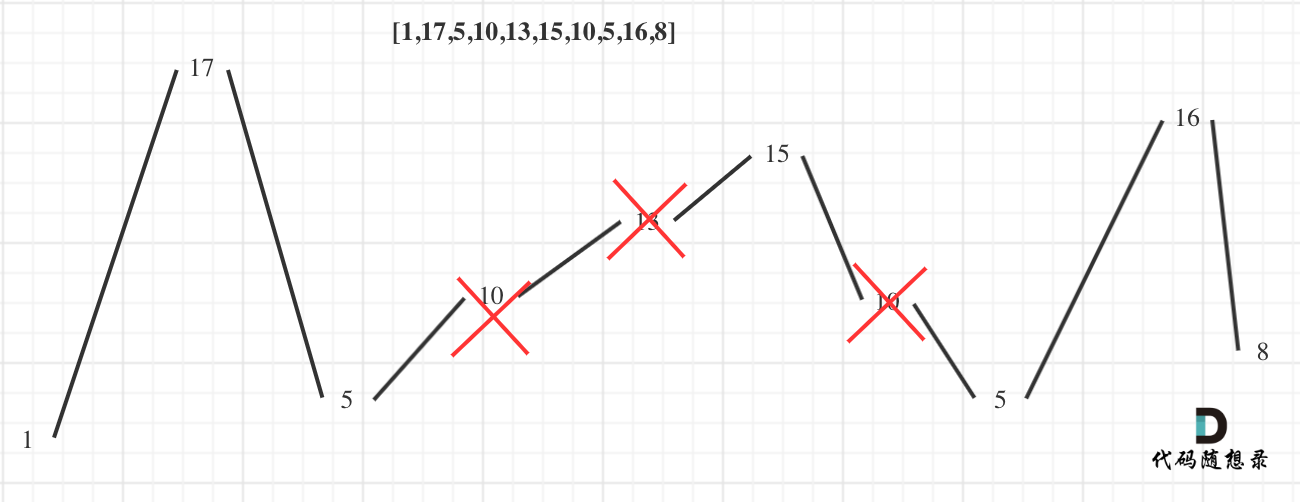
Local Optimality: Delete nodes on the monotonic slope, except for the endpoints, to form two local peaks.
Global Optimality: Maximize the number of local peaks to achieve the longest wiggle sequence.
If local optimal solutions lead to a global optimal solution without counterexamples, using a greedy approach could work!
Practically, there's no need to perform the deletion since we only need the count of peaks (or valleys) for the longest wiggle subsequence (we assume deleting nodes on monotonic slopes and then count the length).
Using this greedy principle, try to keep the peaks as actual peaks and "delete" nodes on a monotonic slope.
In practice, when computing peak count, traverse the index i to compute prediff (nums[i] - nums[i-1]) and curdiff (nums[i+1] - nums[i]). If prediff < 0 && curdiff > 0 or prediff > 0 && curdiff < 0, a wiggle occurs and needs counting.
We have three special situations in this problem:
- Case 1: Plateaus in up and down slopes.
- Case 2: Start and end of the array.
- Case 3: Plateau in a monotonic slope.
# Case 1: Plateaus between up and down
For example: [1,2,2,2,2,1]:
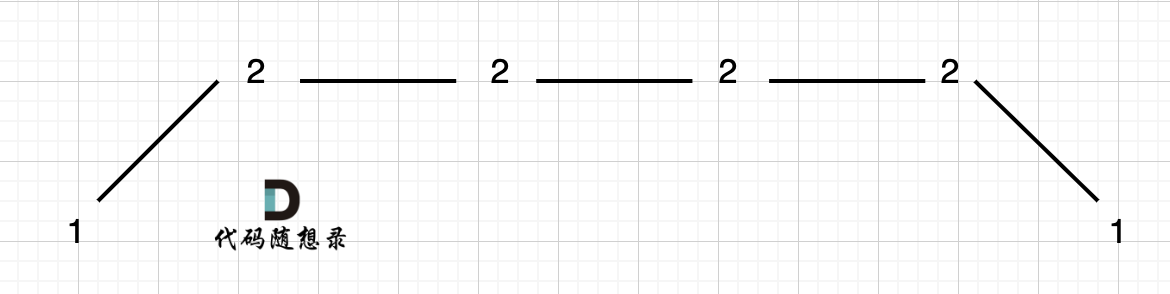
The wiggle sequence length is 3. When dealing with this scenario, either delete the leftmost three 2s or the rightmost ones.
As shown, deleting the leftmost 2s gives:
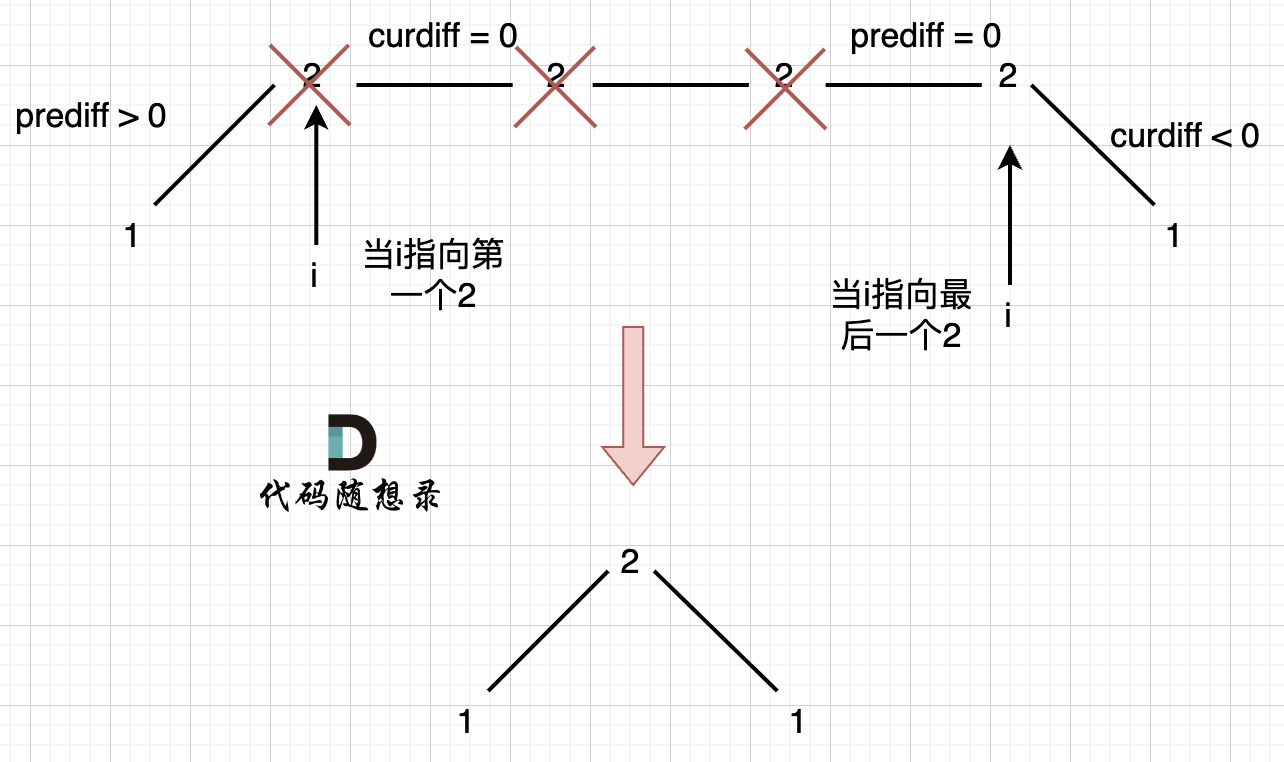
At the first 2, prediff > 0 && curdiff = 0, and at the last 2, prediff = 0 && curdiff < 0.
To achieve a consistent rule: delete the leftmost 2s, meaning when prediff = 0 && curdiff < 0, it is still counting as a peak. This ensures consistency when counting.
So the condition should be (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0), allowing prediff == 0 for such cases.
# Case 2: Start and end of the array
Regarding counting peaks, how to handle the start and end of the array?
For sequences like [2,5], if using difference computation for peaks, handle edge cases.
Tie up: Assume an extra element in front. Suppose it is [2,2,5], thus preDiff = 0, like:
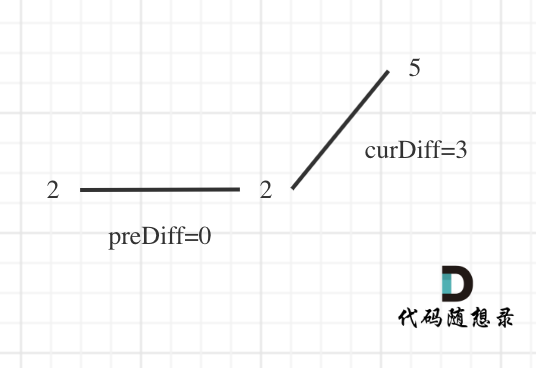
In such cases, the result's default is 1, i.e., assume there's one peak towards the right; then when curDiff > 0 && preDiff <= 0, increment result to count left's peak. The final result is 2.
Given this understanding, here's the code:
// Version 1
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
int curDiff = 0; // Current pair's difference
int preDiff = 0; // Previous pair's difference
int result = 1; // Count of peaks, defaulting to 1
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// A peak occurs
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
result++;
}
preDiff = curDiff;
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
- Time Complexity: O(n)
- Space Complexity: O(1)
If submitted, above code might not pass, hence Situation 3.
# Case 3: Plateau in a monotonic slope
In Version 1, we missed scenarios like: [1,2,2,2,3,4], resulting in wrong peak count.
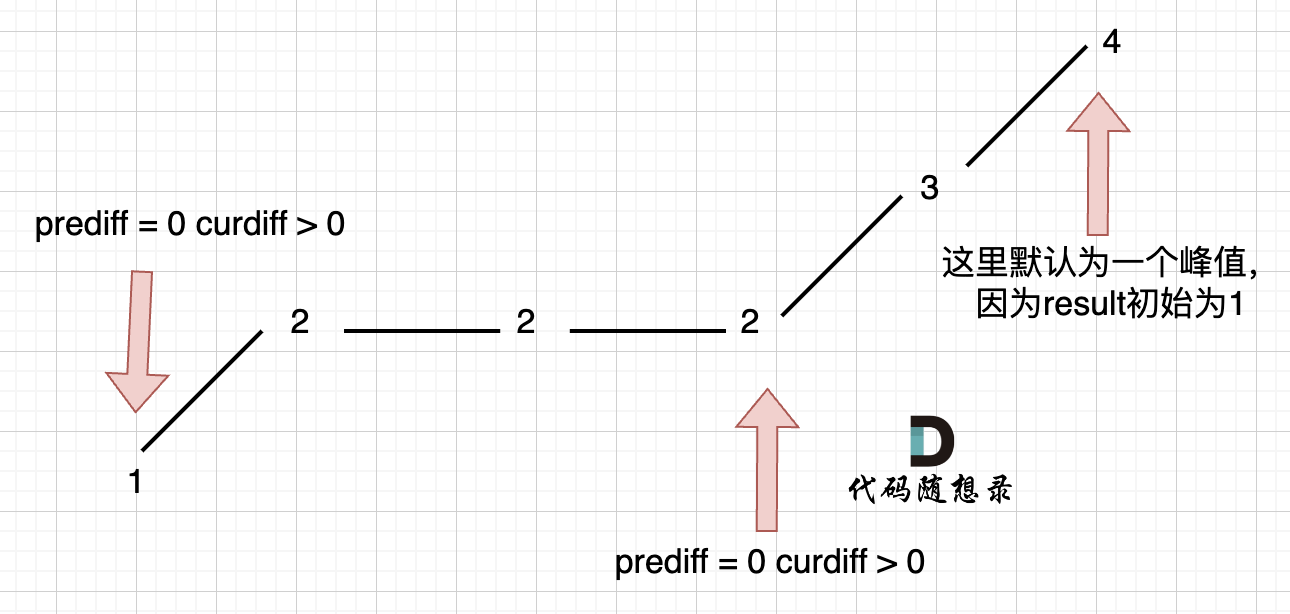
Here, Version 1 inaccurately records three peaks, while actual result is 2.
Misjudge occurs due to updating prediff in real time.
Instead, update prediff during wiggle change, hence it keeps inertia over a plateau, avoiding misinterpretation.
Final solution code:
// Version 2
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
int curDiff = 0; // Current pair's difference
int preDiff = 0; // Previous pair's difference
int result = 1; // Count of peaks, default to 1
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// Peak occurrence conditions
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
result++;
preDiff = curDiff; // Update preDiff only on wiggle change
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
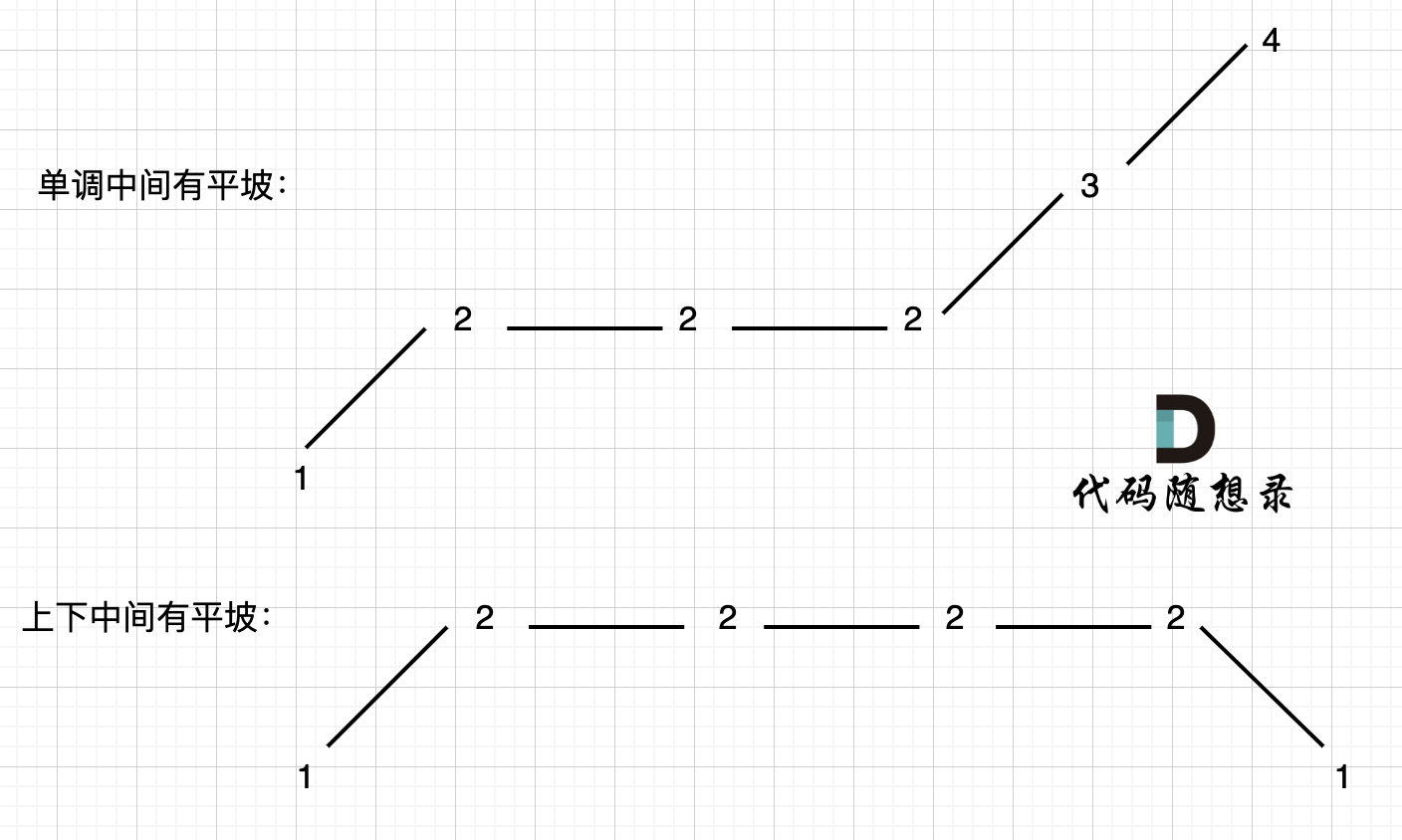
It's complex due to numerous considerations, especially handling plateaus of both types:
# Approach 2 (Dynamic Programming)
Using dynamic programming, recognize:
Either current number forms a peak (nums[i] > nums[i-1]) or a valley (nums[i] < nums[i - 1]).
- Define dp state
dp[i][0]: the maximum wiggle sequence length consideringias a peak. - Define dp state
dp[i][1]: the maximum wiggle sequence length consideringias a valley.
The transition is:
dp[i][0] = max(dp[i][0], dp[j][1] + 1), conditioned on0 < j < iandnums[j] < nums[i](attachnums[i]as peak after valleyj).dp[i][1] = max(dp[i][1], dp[j][0] + 1), conditioned on0 < j < iandnums[j] > nums[i](attachnums[i]as valley after peakj).
Base cases:
Starting as a single element sequence with itself, dp[0][0] = dp[0][1] = 1.
C++ Implementation:
class Solution {
public:
int dp[1005][2];
int wiggleMaxLength(vector<int>& nums) {
memset(dp, 0, sizeof dp);
dp[0][0] = dp[0][1] = 1;
for (int i = 1; i < nums.size(); ++i) {
dp[i][0] = dp[i][1] = 1;
for (int j = 0; j < i; ++j) {
if (nums[j] > nums[i]) dp[i][1] = max(dp[i][1], dp[j][0] + 1);
}
for (int j = 0; j < i; ++j) {
if (nums[j] < nums[i]) dp[i][0] = max(dp[i][0], dp[j][1] + 1);
}
}
return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- Time Complexity: O(n^2)
- Space Complexity: O(n)
Advanced
Utilize two segment trees to maintain a maximum range value:
- Update
tree1atnums[i]fordp[i][0]. - Update
tree2atnums[i]fordp[i][1]. - Eliminate iterations over
jby querying trees directly.
Time Complexity: O(nlog n)
Space Complexity: O(n)
# Other Language Versions
# Java
class Solution {
public int wiggleMaxLength(int[] nums) {
if (nums.length <= 1) {
return nums.length;
}
// current difference
int curDiff = 0;
// previous difference
int preDiff = 0;
int count = 1;
for (int i = 1; i < nums.length; i++) {
// obtain current difference
curDiff = nums[i] - nums[i - 1];
// if current and previous differences have opposite signs
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
count++;
preDiff = curDiff;
}
}
return count;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// DP
class Solution {
public int wiggleMaxLength(int[] nums) {
// 0 i represents the length when i is a peak
// 1 i represents the length when i is a valley
int dp[][] = new int[nums.length][2];
dp[0][0] = dp[0][1] = 1;
for (int i = 1; i < nums.length; i++){
// i itself can be a peak or a valley
dp[i][0] = dp[i][1] = 1;
for (int j = 0; j < i; j++){
if (nums[j] > nums[i]){
// i is a valley
dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
}
if (nums[j] < nums[i]){
// i is a peak
dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
}
}
}
return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Python
Greedy (Version 1)
class Solution:
def wiggleMaxLength(self, nums):
if len(nums) <= 1:
return len(nums) # Return if array length is 0 or 1
curDiff = 0 # Current pair's difference
preDiff = 0 # Previous pair's difference
result = 1 # Count of peaks, default to 1
for i in range(len(nums) - 1):
curDiff = nums[i + 1] - nums[i] # Difference with next element
# If a peak occurs
if (preDiff <= 0 and curDiff > 0) or (preDiff >= 0 and curDiff < 0):
result += 1 # Increment peak count
preDiff = curDiff # Update preDiff only on wiggle change
return result # Return longest wiggle sequence length
2
3
4
5
6
7
8
9
10
11
12
13
14
Greedy (Version 2)
class Solution:
def wiggleMaxLength(self, nums: List[int]) -> int:
if len(nums) <= 1:
return len(nums) # If length is 0 or 1
preDiff, curDiff, result = 0, 0, 1 # Initialize
for i in range(len(nums) - 1):
curDiff = nums[i + 1] - nums[i]
if curDiff * preDiff <= 0 and curDiff != 0: # No wiggle if zero
result += 1
preDiff = curDiff # Update preDiff only when differing sign
return result
2
3
4
5
6
7
8
9
10
11
Dynamic Programming (Version 1)
class Solution:
def wiggleMaxLength(self, nums: List[int]) -> int:
# 0 i is a peak
# 1 i is a valley
dp = []
for i in range(len(nums)):
dp.append([1, 1])
for j in range(i):
if nums[j] > nums[i]:
dp[i][1] = max(dp[i][1], dp[j][0] + 1)
if nums[j] < nums[i]:
dp[i][0] = max(dp[i][0], dp[j][1] + 1)
return max(dp[-1][0], dp[-1][1])
2
3
4
5
6
7
8
9
10
11
12
13
Dynamic Programming (Version 2)
class Solution:
def wiggleMaxLength(self, nums):
dp = [[0, 0] for _ in range(len(nums))] # DP array to track longest sequences
dp[0][0] = dp[0][1] = 1 # Initialize, defaulting to single element peaks
for i in range(1, len(nums)):
dp[i][0] = dp[i][1] = 1 # Base case for each i
for j in range(i):
if nums[j] > nums[i]:
dp[i][1] = max(dp[i][1], dp[j][0] + 1) # Valley condition
for j in range(i):
if nums[j] < nums[i]:
dp[i][0] = max(dp[i][0], dp[j][1] + 1) # Peak condition
return max(dp[-1][0], dp[-1][1]) # Return max for last element
2
3
4
5
6
7
8
9
10
11
12
13
Dynamic Programming (Version 3) Optimization
class Solution:
def wiggleMaxLength(self, nums):
if len(nums) <= 1:
return len(nums) # Edge case for length <= 1
up = down = 1 # Start with base cases
for i in range(1, len(nums)): # Go through array
if nums[i] < nums[i - 1]: # Valley
down = max(up + 1, down)
if nums[i] > nums[i - 1]: # Peak
up = max(down + 1, up)
return max(up, down) # Return max of peak and valley
2
3
4
5
6
7
8
9
10
11
# Go
Greedy
func wiggleMaxLength(nums []int) int {
n := len(nums)
if n < 2 {
return n
}
ans := 1
prevDiff := nums[1] - nums[0]
if prevDiff != 0 {
ans = 2
}
for i := 2; i < n; i++ {
diff := nums[i] - nums[i-1]
if diff > 0 && prevDiff <= 0 || diff < 0 && prevDiff >= 0 {
ans++
prevDiff = diff
}
}
return ans
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Dynamic Programming
func wiggleMaxLength(nums []int) int {
n := len(nums)
if n <= 1 {
return n
}
dp := make([][2]int, n)
// i 0 represents the length when i is a peak
// i 1 represents the length when i is a valley
dp[0][0] = 1
dp[0][1] = 1
for i := 0; i < n; i++ {
for j := 0; j < i; j++ {
if nums[j] > nums[i] { // nums[i] as a valley
dp[i][1] = max(dp[i][1], dp[j][0]+1)
}
if nums[j] < nums[i] { // nums[i] as a peak or equal
dp[i][0] = max(dp[i][0], dp[j][1]+1)
}
if nums[j] == nums[i] { // when nums[i] is equal
dp[i][0] = max(dp[i][0], dp[j][0]) // Peak
dp[i][1] = max(dp[i][1], dp[j][1]) // Valley
}
}
}
return max(dp[n-1][0], dp[n-1][1])
}
func max(a, b int) int {
if a > b {
return a
} else {
return b
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# JavaScript
Greedy
var wiggleMaxLength = function(nums) {
if(nums.length <= 1) return nums.length
let result = 1
let preDiff = 0
let curDiff = 0
for(let i = 0; i < nums.length - 1; i++) {
curDiff = nums[i + 1] - nums[i]
if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
result++
preDiff = curDiff
}
}
return result
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Dynamic Programming
var wiggleMaxLength = function(nums) {
if (nums.length === 1) return 1;
// 0 i represents the length when i is a peak
// 1 i represents the length when i is a valley
let down = 1;
let up = 1;
for (let i = 1; i < nums.length; i++) {
if (nums[i] < nums[i - 1]) {
down = Math.max(up + 1, down);
}
if (nums[i] > nums[i - 1]) {
up = Math.max(down + 1, up)
}
}
return Math.max(down, up);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Rust
Greedy
impl Solution {
pub fn wiggle_max_length(nums: Vec<i32>) -> i32 {
if nums.len() == 1 {
return 1;
}
let mut res = 1;
let mut pre_diff = 0;
for i in 0..nums.len() - 1 {
let cur_diff = nums[i + 1] - nums[i];
if (pre_diff <= 0 && cur_diff > 0) || (pre_diff >= 0 && cur_diff < 0) {
res += 1;
pre_diff = cur_diff;
}
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Dynamic Programming
impl Solution {
pub fn wiggle_max_length(nums: Vec<i32>) -> i32 {
if nums.len() == 1 {
return 1;
}
let (mut down, mut up) = (1, 1);
for i in 1..nums.len() {
// i - 1 is a peak
if nums[i] < nums[i - 1] {
down = down.max(up + 1);
}
// i - 1 is a valley
if nums[i] > nums[i - 1] {
up = up.max(down + 1);
}
}
down.max(up)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# C
Greedy
int wiggleMaxLength(int* nums, int numsSize){
if(numsSize <= 1)
return numsSize;
int length = 1;
int preDiff , curDiff;
preDiff = curDiff = 0;
for(int i = 0; i < numsSize - 1; ++i) {
// Calculate the difference for the current i and i+1 elements
curDiff = nums[i+1] - nums[i];
// If preDiff and curDiff have opposite signs, increment length. Update the sign of preDiff
// If preDiff and curDiff have the same sign, the current i element is the middle of a continuous increasing/decreasing subsequence.
// Note: When preDiff is 0, whether curDiff is positive or negative counts as opposite signs
if((curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0)) {
preDiff = curDiff;
length++;
}
}
return length;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Dynamic Programming
int max(int left, int right)
{
return left > right ? left : right;
}
int wiggleMaxLength(int* nums, int numsSize){
if(numsSize <= 1)
{
return numsSize;
}
// 0 i is a peak
// 1 i is a valley
int dp[numsSize][2];
for(int i = 0; i < numsSize; i++)
{
dp[i][0] = 1;
dp[i][1] = 1;
for(int j = 0; j < i; j++)
{
// nums[i] is a valley
if(nums[j] > nums[i])
{
dp[i][1] = max(dp[i][1], dp[j][0] + 1);
}
// nums[i] is a peak
if(nums[j] < nums[i])
{
dp[i][0] = max(dp[i][0], dp[j][1] + 1);
}
}
}
return max(dp[numsSize - 1][0], dp[numsSize - 1][1]);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# TypeScript
Greedy
function wiggleMaxLength(nums: number[]): number {
let length: number = nums.length;
if (length <= 1) return length;
let preDiff: number = 0;
let curDiff: number = 0;
let count: number = 1;
for (let i = 1; i < length; i++) {
curDiff = nums[i] - nums[i - 1];
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
preDiff = curDiff;
count++;
}
}
return count;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Dynamic Programming
function wiggleMaxLength(nums: number[]): number {
const length: number = nums.length;
if (length <= 1) return length;
const dp: number[][] = new Array(length).fill(0).map((_) => []);
dp[0][0] = 1; // when the first number is a peak
dp[0][1] = 1; // when the first number is a valley
for (let i = 1; i < length; i++) {
dp[i][0] = 1;
dp[i][1] = 1;
for (let j = 0; j < i; j++) {
if (nums[j] < nums[i]) dp[i][0] = Math.max(dp[i][0], dp[j][1] + 1);
}
for (let j = 0; j < i; j++) {
if (nums[j] > nums[i]) dp[i][1] = Math.max(dp[i][1], dp[j][0] + 1);
}
}
return Math.max(dp[length - 1][0], dp[length - 1][1]);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Scala
object Solution {
def wiggleMaxLength(nums: Array[Int]): Int = {
if (nums.length <= 1) return nums.length
var result = 1
var curDiff = 0 // Current pair's difference
var preDiff = 0 // Previous pair's difference
for (i <- 1 until nums.length) {
curDiff = nums(i) - nums(i - 1) // Calculate current pair's diff
// When curDiff > 0, preDiff must be <= 0
// When curDiff < 0, preDiff must be >= 0
// These conditions indicate two peaks
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
result += 1 // Increment result
preDiff = curDiff // Assign current difference to the last round
}
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C#
public class Solution
{
public int WiggleMaxLength(int[] nums)
{
if (nums.Length < 2) return nums.Length;
int curDiff = 0, preDiff = 0, res = 1;
for (int i = 0; i < nums.Length - 1; i++)
{
curDiff = nums[i + 1] - nums[i];
if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0))
{
res++;
preDiff = curDiff;
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
