1382. Balance a Binary Search Tree

LeetCode Problem Link (opens new window)

Given a binary search tree, return a balanced binary search tree with the same node values. If there are multiple ways to achieve this, return any one of them.

A binary search tree is considered balanced if the height difference between the left and right subtrees for every node is no more than 1.

Example:

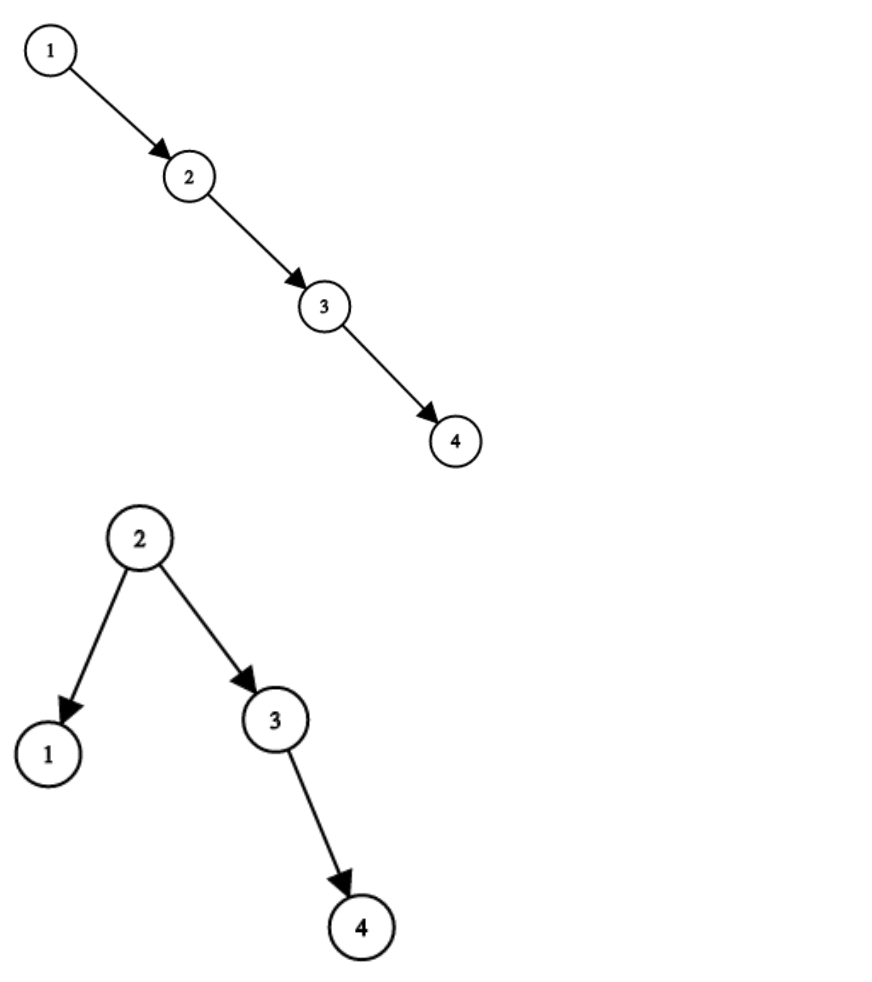
• Input: root = [1,null,2,null,3,null,4,null,null]
• Output: [2,1,3,null,null,null,4]
• Explanation: This is not the only correct answer; [3,1,4,null,2,null,null] is also a valid solution.

Constraints:

• The number of nodes in the tree is between 1 and 10^4.
• Node values are unique and between 1 and 10^5.

Solution

To solve this problem, we can perform an inorder traversal to convert the binary tree into a sorted array and then construct a balanced binary search tree from the sorted array.

Before attempting this problem, it's recommended to review the following two explanations:

• 0098.Validate Binary Search Tree (opens new window) to understand the properties of a binary search tree.
• 0108.Convert Sorted Array to Binary Search Tree (opens new window) to learn how to construct a balanced binary search tree from a sorted array.

After understanding these, this problem will be straightforward.

Here is the code:

class Solution {
private:
    vector<int> vec;
    // Convert binary tree to sorted array
    void traversal(TreeNode* cur) {
        if (cur == nullptr) {
            return;
        }
        traversal(cur->left);
        vec.push_back(cur->val);
        traversal(cur->right);
    }
    // Convert sorted array to balanced binary search tree
    TreeNode* getTree(vector<int>& nums, int left, int right) {
        if (left > right) return nullptr;
        int mid = left + ((right - left) / 2);
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = getTree(nums, left, mid - 1);
        root->right = getTree(nums, mid + 1, right);
        return root;
    }

public:
    TreeNode* balanceBST(TreeNode* root) {
        traversal(root);
        return getTree(vec, 0, vec.size() - 1);
    }
};

Other Language Versions

Java:

class Solution {
    ArrayList <Integer> res = new ArrayList<Integer>();
    // Convert binary tree to sorted array
    private void travesal(TreeNode cur) {
            if (cur == null) return;
            travesal(cur.left);
            res.add(cur.val);
            travesal(cur.right);
        }
    // Convert sorted array to balanced binary search tree
    private TreeNode getTree(ArrayList <Integer> nums, int left, int right) {
        if (left > right) return null;
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums.get(mid));
        root.left = getTree(nums, left, mid - 1);
        root.right = getTree(nums, mid + 1, right);
        return root;
    }
    public TreeNode balanceBST(TreeNode root) {
        travesal(root);
        return getTree(res, 0, res.size() - 1);
    }
}

Python:

class Solution:
    def balanceBST(self, root: TreeNode) -> TreeNode:
        res = []
        # Convert binary tree to sorted array
        def traversal(cur: TreeNode):
            if not cur: return
            traversal(cur.left)
            res.append(cur.val)
            traversal(cur.right)
        # Convert sorted array to balanced binary search tree
        def getTree(nums: List, left, right):
            if left > right: return 
            mid = left + (right -left) // 2
            root = TreeNode(nums[mid])
            root.left = getTree(nums, left, mid - 1)
            root.right = getTree(nums, mid + 1, right)
            return root
        traversal(root)
        return getTree(res, 0, len(res) - 1)

Go:

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func balanceBST(root *TreeNode) *TreeNode {
   // Convert binary tree to sorted array
	nums := []int{}
   // Inorder traversal
	var travel func(node *TreeNode)
	travel = func(node *TreeNode) {
		if node == nil {
			return
		}
		travel(node.Left)
		nums = append(nums, node.Val)
		travel(node.Right)
	}
	// Construct balanced binary search tree using binary search
	var buildTree func(nums []int, left, right int) *TreeNode
	buildTree = func(nums []int, left, right int) *TreeNode {
		if left > right {
			return nil
		}
		mid := left + (right-left) >> 1
		root := &TreeNode{Val: nums[mid]}
		root.Left = buildTree(nums, left, mid-1)
		root.Right = buildTree(nums, mid+1, right)
		return root
	}
	travel(root)
	return buildTree(nums, 0, len(nums)-1)
}

JavaScript:

var balanceBST = function(root) {
    const res = [];
    // Inorder traversal to convert to a sorted array
    const travesal = cur => {
        if(!cur) return;
        travesal(cur.left);
        res.push(cur.val);
        travesal(cur.right);
    }
    // Construct a balanced binary search tree from the sorted array
    const getTree = (nums, left, right) => {
        if(left > right) return null;
        let mid = left + ((right - left) >> 1);
        let root = new TreeNode(nums[mid]);// Use the middle element as the current node value
        root.left = getTree(nums, left, mid - 1);// Recursively create the left subtree
        root.right = getTree(nums, mid + 1, right);// Recursively create the right subtree
        return root;
    }
    travesal(root);
    return getTree(res, 0, res.length - 1);
};

TypeScript:

function balanceBST(root: TreeNode | null): TreeNode | null {
    const inorderArr: number[] = [];
    inorderTraverse(root, inorderArr);
    return buildTree(inorderArr, 0, inorderArr.length - 1);
};
function inorderTraverse(node: TreeNode | null, arr: number[]): void {
    if (node === null) return;
    inorderTraverse(node.left, arr);
    arr.push(node.val);
    inorderTraverse(node.right, arr);
}
function buildTree(arr: number[], left: number, right: number): TreeNode | null {
    if (left > right) return null;
    const mid = (left + right) >> 1;
    const resNode: TreeNode = new TreeNode(arr[mid]);
    resNode.left = buildTree(arr, left, mid - 1);
    resNode.right = buildTree(arr, mid + 1, right);
    return resNode;
}