# 704. Binary Search
LeetCode Problem Link (opens new window)
Given an n element sorted (in ascending order) integer array nums and a target value target, write a function to search target in nums. If the target value exists, return its index; otherwise, return -1.
Example 1:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4.
2
3
Example 2:
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums, so return -1.
2
3
Constraints:
- You may assume that all elements in nums are unique.
nwill be in the range[1, 10000].- Each element of nums will be in the range
[-9999, 9999].
# Approach
This problem's prerequisite is that the array is sorted, and the problem emphasizes that there are no duplicate elements in the array. This is important because if there are duplicate elements, the index returned by binary search might not be unique, which is a prerequisite condition for using the binary search method. When you see these conditions in a problem statement, you should consider whether binary search can be applied.
Binary search involves many edge cases, and though logically simple, it can be difficult to write correctly. For example, should you use while(left < right) or while(left <= right)? Should you set right = middle or right = middle - 1?
Many people struggle with binary search because they don't clearly understand the definition of the interval. The definition of the interval is the invariant. Maintaining this invariant throughout the binary search process means handling borders based on this interval definition in each iteration of the loop. This is known as the invariant loop rule.
In binary search, the interval is usually defined in two ways: closed on both sides, i.e., [left, right], or closed on the left and open on the right, i.e., [left, right).
Below, I will explain each definition and how they affect the binary search algorithm.
# Binary Search - First Method
In the first method, we define the target value to be within a closed interval [left, right].
The interval definition determines how the binary search code should be written because our target is defined within [left, right], so:
- Use
while (left <= right)becauseleft == rightis meaningful, so we use<=. - If
nums[middle] > target, thenrightshould be set tomiddle - 1becausenums[middle]is definitely not the target. Hence, the ending index of the left search interval becomesmiddle - 1.
For example, if searching for the element 2 in the array: 1,2,3,4,7,9,10:
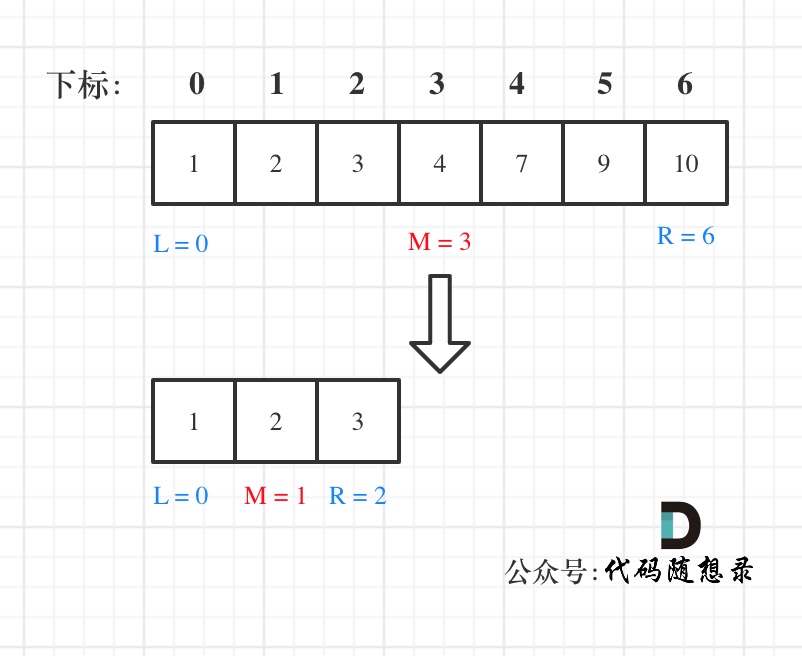
Below is the code with detailed comments:
// Version 1
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1; // target is in [left, right]
while (left <= right) { // [left, right] is valid when left == right, so use <=
int middle = left + ((right - left) / 2); // prevent overflow, the same as (left + right) / 2
if (nums[middle] > target) {
right = middle - 1; // target is in the left interval, so [left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target is in the right interval, so [middle + 1, right]
} else { // nums[middle] == target
return middle; // target value found in the array, return index
}
}
// target not found
return -1;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- Time complexity: O(log n)
- Space complexity: O(1)
# Binary Search - Second Method
If the target is within a left-closed, right-open interval [left, right), the boundary handling in the binary search algorithm is different:
- Use
while (left < right), because whenleft == rightin[left, right), it's an invalid range, so we use<. - If
nums[middle] > target, thenrightis updated tomiddle, becausenums[middle]is not equal to the target. Continuing to search the left section, and since the search range is left-closed, right-open, right updates tomiddle. Thus, the next search range does not includenums[middle].
In the array: 1,2,3,4,7,9,10, when searching for the element 2:
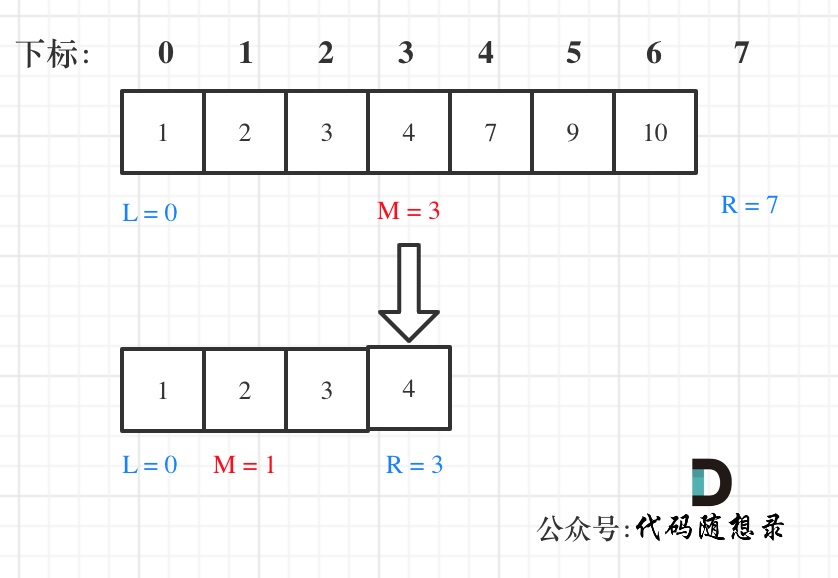
The code is as follows, with detailed comments:
// Version 2
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size(); // define target in [left, right)
while (left < right) { // [left, right) is invalid when left == right, hence use <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target is in the left interval, [left, middle)
} else if (nums[middle] < target) {
left = middle + 1; // target is in the right interval, [middle + 1, right)
} else { // nums[middle] == target
return middle; // target value found in the array, return index
}
}
// target not found
return -1;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- Time complexity: O(log n)
- Space complexity: O(1)
# Conclusion
Binary search is a very foundational algorithm, and many struggle with grasping the concept but faltering in implementation because they don't clearly understand the definitions of intervals. The interval definition is the invariant; adhering to this interval definition consistently when making boundary decisions in the loop is the invariant loop rule.
This article provides two common interval definitions and corresponding binary search methods, with detailed explanations for each boundary handling based on the interval definition.
It's hoped that after reading this article, you'll have a deeper understanding of binary search.
# Related Problem Recommendations
- 0035.Search Insert Position (opens new window)
- 34. Find First and Last Position of Element in Sorted Array (opens new window)
- 69. Sqrt(x) (opens new window)
- 367. Valid Perfect Square (opens new window)
Other Language Versions
# Java:
(Version 1) Closed Interval
class Solution {
public int search(int[] nums, int target) {
// Avoid unnecessary loops when target is less than nums[0] or more than nums[nums.length - 1]
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}
else if (nums[mid] < target) {
left = mid + 1;
}
else { // nums[mid] > target
right = mid - 1;
}
}
// target not found
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
(Version 2) Left Closed, Right Open Interval
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] == target) {
return mid;
}
else if (nums[mid] < target) {
left = mid + 1;
}
else { // nums[mid] > target
right = mid;
}
}
// target not found
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Python:
(Version 1) Closed Interval
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1 # target is in [left, right]
while left <= right:
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle - 1 # target is in [left, middle - 1]
elif nums[middle] < target:
left = middle + 1 # target is in [middle + 1, right]
else:
return middle # target value found in array, return index
return -1 # target not found
2
3
4
5
6
7
8
9
10
11
12
13
14
(Version 2) Left Closed, Right Open Interval
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) # target in [left, right)
while left < right: # left == right is an invalid range in [left, right), so use <
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle # target is in left interval [left, middle)
elif nums[middle] < target:
left = middle + 1 # target is in right interval [middle + 1, right)
else:
return middle # target value found in array, return index
return -1 # target not found
2
3
4
5
6
7
8
9
10
11
12
13
14
# Go:
(Version 1) Closed Interval
// Time Complexity O(logn)
func search(nums []int, target int) int {
// Initialize borders
left := 0
right := len(nums) - 1
// Loop and gradually narrow interval range
for left <= right {
// Calculate midpoint of interval
mid := left + (right-left)>>1
// Adjust interval range based on nums[mid] and target
if nums[mid] == target {
return mid
} else if nums[mid] < target {
left = mid + 1
} else {
right = mid - 1
}
}
// target not found in input array
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
(Version 2) Left Closed, Right Open Interval
// Time Complexity O(logn)
func search(nums []int, target int) int {
// Initialize borders
left := 0
right := len(nums)
// Loop and gradually narrow interval range
for left < right {
// Calculate midpoint of interval
mid := left + (right-left)>>1
// Adjust interval range based on nums[mid] and target
if nums[mid] == target {
return mid
} else if nums[mid] < target {
left = mid + 1
} else {
right = mid
}
}
// target not found in input array
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# JavaScript:
(Version 1) Closed Interval [left, right]
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function(nums, target) {
// right is the index of the last number in the array; num[right] is within the search range, which is a closed interval
let mid, left = 0, right = nums.length - 1;
// the case of left=right is justified since nums[right] is within the search range
while (left <= right) {
// bitwise operation + prevent large number overflow
mid = left + ((right - left) >> 1);
// if the middle number is greater than the target, exclude the middle number from the search; therefore, update right boundary as mid-1
if (nums[mid] > target) {
right = mid - 1; // search in the left closed interval
} else if (nums[mid] < target) {
left = mid + 1; // search in the right closed interval
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
(Version 2) Left Closed, Right Open Interval [left, right)
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function(nums, target) {
// right is the index of the last number in the array plus one; nums[right] is not within the search range, which is a left closed, right open interval
let mid, left = 0, right = nums.length;
// when left equals right, nums[right] is not in search range, so do not need to cover this case
while (left < right) {
// bitwise operation + prevent large number overflow
mid = left + ((right - left) >> 1);
// if middle value is greater than target, exclude middle value from the next search range, but the preceding value should remain;
// because right is originally not within the search range, update right to the middle value. If right is updated to mid-1, the preceding value is also excluded from the search range.
if (nums[mid] > target) {
right = mid; // search in the left section
} else if (nums[mid] < target) {
left = mid + 1; // search in the right section
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# TypeScript
(Version 1) Closed Interval
function search(nums: number[], target: number): number {
let mid: number, left: number = 0, right: number = nums.length - 1;
while (left <= right) {
// bitwise operation + prevent large number overflow
mid = left + ((right - left) >> 1);
if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(Version 2) Left Closed, Right Open Interval
function search(nums: number[], target: number): number {
let mid: number, left: number = 0, right: number = nums.length;
while (left < right) {
// bitwise operation + prevent large number overflow
mid = left +((right - left) >> 1);
if (nums[mid] > target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
return mid;
}
}
return -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Ruby:
# (Version 1) Closed Interval
def search(nums, target)
left, right = 0, nums.length - 1
while left <= right # target is in a closed interval, so an extreme case exists where left==right
middle = (left + right) / 2
if nums[middle] > target
right = middle - 1
elsif nums[middle] < target
left = middle + 1
else
return middle # return acts as return and breaks loop simultaneously
end
end
-1
end
# (Version 2) Left Closed, Right Open Interval
def search(nums, target)
left, right = 0, nums.length
while left < right # there exists an extreme case where right=left+1, so < is used to avoid this case
middle = (left + right) / 2
if nums[middle] > target
right = middle
elsif nums[middle] < target
left = middle + 1
else
return middle
end
end
-1
end
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Swift:
// (Version 1) Closed Interval
func search(nums: [Int], target: Int) -> Int {
// 1. Define interval. Here the interval is [left, right]
var left = 0
var right = nums.count - 1
while left <= right { // Since target is in [left, right], including left == right is meaningful, hence <=
// 2. Calculate mid index (If both left and right are large, left + right may overflow)
// let middle = (left + right) / 2
// Prevent overflow:
let middle = left + (right - left) / 2
// 3. Determine
if target < nums[middle] {
// If target is in the left section, update the right bound, new section is [left, middle - 1]
right = middle - 1
} else if target > nums[middle] {
// If target is in the right section, update the left bound, new section is [middle + 1, right]
left = middle + 1
} else {
// If target is in the middle, return the middle index
return middle
}
}
// If target not found, return -1
return -1
}
// (Version 2) Left Closed, Right Open Interval
func search(nums: [Int], target: Int) -> Int {
var left = 0
var right = nums.count
while left < right {
let middle = left + ((right - left) >> 1)
if target < nums[middle] {
right = middle
} else if target > nums[middle] {
left = middle + 1
} else {
return middle
}
}
return -1
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# Rust:
(Version 1) Closed Interval
use std::cmp::Ordering;
impl Solution {
pub fn search(nums: Vec<i32>, target: i32) -> i32 {
let (mut left, mut right) = (0_i32, nums.len() as i32 - 1);
while left <= right {
let mid = (right + left) / 2;
match nums[mid as usize].cmp(&target) {
Ordering::Less => left = mid + 1,
Ordering::Greater => right = mid - 1,
Ordering::Equal => return mid,
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//(Version 2) Left Closed, Right Open Interval
use std::cmp::Ordering;
impl Solution {
pub fn search(nums: Vec<i32>, target: i32) -> i32 {
let (mut left, mut right) = (0_i32, nums.len() as i32);
while left < right {
let mid = (right + left) / 2;
match nums[mid as usize].cmp(&target) {
Ordering::Less => left = mid + 1,
Ordering::Greater => right = mid,
Ordering::Equal => return mid,
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# C:
// (Version 1) Closed Interval [left, right]
int search(int* nums, int numsSize, int target){
int left = 0;
int right = numsSize-1;
int middle = 0;
// if left is less than or equal to right, it means the interval contains elements
while(left<=right) {
// update the value of search index middle
middle = (left+right)/2;
// target may be in the interval [left,middle-1]
if(nums[middle] > target) {
right = middle-1;
}
// target may be in the interval [middle+1,right]
else if(nums[middle] < target) {
left = middle+1;
}
// current index element equals target value, return middle
else if(nums[middle] == target){
return middle;
}
}
// return -1 if target element is not found
return -1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// (Version 2) Left Closed, Right Open Interval [left, right)
int search(int* nums, int numsSize, int target){
int length = numsSize;
int left = 0;
int right = length; // define target within [left, right)
int middle = 0;
while(left < right){ // when left equals right, [left, right) is an empty set, so use <
int middle = left + (right - left) / 2;
if(nums[middle] < target){
// target is within (middle , right), guarantee the section is left closed, right open, equivalent to [middle + 1,right)
left = middle + 1;
}else if(nums[middle] > target){
// target is within [left, middle)
right = middle ;
}else{ // nums[middle] == target, target value found
return middle;
}
}
// return -1 if target not found
return -1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# PHP:
// Closed Interval
class Solution {
/**
* @param Integer[] $nums
* @param Integer $target
* @return Integer
*/
function search($nums, $target) {
if (count($nums) == 0) {
return -1;
}
$left = 0;
$right = count($nums) - 1;
while ($left <= $right) {
$mid = floor(($left + $right) / 2);
if ($nums[$mid] == $target) {
return $mid;
}
if ($nums[$mid] > $target) {
$right = $mid - 1;
}
else {
$left = $mid + 1;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# C#:
//Closed Interval
public class Solution {
public int Search(int[] nums, int target) {
int left = 0;
int right = nums.Length - 1;
while(left <= right){
int mid = (right - left ) / 2 + left;
if(nums[mid] == target){
return mid;
}
else if(nums[mid] < target){
left = mid+1;
}
else if(nums[mid] > target){
right = mid-1;
}
}
return -1;
}
}
//Left Closed, Right Open Interval
public class Solution{
public int Search(int[] nums, int target){
int left = 0;
int right = nums.Length;
while(left < right){
int mid = (right - left) / 2 + left;
if(nums[mid] == target){
return mid;
}
else if(nums[mid] < target){
left = mid + 1;
}
else if(nums[mid] > target){
right = mid;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# Kotlin:
class Solution {
fun search(nums: IntArray, target: Int): Int {
// leftBorder
var left:Int = 0
// rightBorder
var right:Int = nums.size - 1
// using left closed, right closed interval
while (left <= right) {
var middle:Int = left + (right - left)/2
// target is on the left
if (nums[middle] > target) {
right = middle - 1
}
else {
// target is on the right
if (nums[middle] < target) {
left = middle + 1
}
// found, return
else return middle
}
}
// not found, return
return -1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Kotlin:
// (Version 1) Left Closed, Right Open Interval
class Solution {
fun search(nums: IntArray, target: Int): Int {
var left = 0
var right = nums.size // [left,right) right is a non-inclusive interval, set right to nums.size
while (left < right) {
val mid = (left + right) / 2
if (nums[mid] < target) left = mid + 1
else if (nums[mid] > target) right = mid // Crucial part: right is a non-inclusive interval in the loop
else return mid
}
return -1 // target not found, return -1
}
}
// (Version 2) Closed Interval
class Solution {
fun search(nums: IntArray, target: Int): Int {
var left = 0
var right = nums.size - 1 // [left,right] right is an inclusive interval, set right to nums.size - 1
while (left <= right) {
val mid = (left + right) / 2
if (nums[mid] < target) left = mid + 1
else if (nums[mid] > target) right = mid - 1 // Crucial part: right is inclusive in the loop
else return mid
}
return -1 // target not found, return -1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Scala:
(Version 1) Closed Interval
object Solution {
def search(nums: Array[Int], target: Int): Int = {
var left = 0
var right = nums.length - 1
while (left <= right) {
var mid = left + ((right - left) / 2)
if (target == nums(mid)) {
return mid
} else if (target < nums(mid)) {
right = mid - 1
} else {
left = mid + 1
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(Version 2) Left Closed, Right Open Interval
object Solution {
def search(nums: Array[Int], target: Int): Int = {
var left = 0
var right = nums.length
while (left < right) {
val mid = left + (right - left) / 2
if (target == nums(mid)) {
return mid
} else if (target < nums(mid)) {
right = mid
} else {
left = mid + 1
}
}
-1
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Dart:
(Version 1) Closed Interval
class Solution {
int search(List<int> nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int middle = ((left + right)/2).truncate();
switch (nums[middle].compareTo(target)) {
case 1:
right = middle - 1;
continue;
case -1:
left = middle + 1;
continue;
default:
return middle;
}
}
return -1;
}
}
(Version 2) Left Closed, Right Open Interval
class Solution {
int search(List<int> nums, int target) {
int left = 0;
int right = nums.length;
while (left < right) {
int middle = left + ((right - left) >> 1);
switch (nums[middle].compareTo(target)) {
case 1:
right = middle;
continue;
case -1:
left = middle + 1;
continue;
default:
return middle;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
