# 209. Minimum Size Subarray Sum
LeetCode Problem Link (opens new window)
Given an array of n positive integers and a positive integer s, find the minimal length of a contiguous subarray for which the sum is greater than or equal to s. If there isn’t one, return 0 instead.
Example:
- Input:
s = 7, nums = [2,3,1,2,4,3] - Output:
2 - Explanation: The subarray
[4,3]has the minimal length under the problem constraints.
Constraints:
1 <= target <= 10^91 <= nums.length <= 10^51 <= nums[i] <= 10^5
# Solution
# Brute Force Solution
The brute force solution involves two nested for loops to continually search for subarrays that meet the desired condition. The time complexity is obviously O(n^2).
Here is the code:
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX; // the final result
int sum = 0; // sum of the subarray
int subLength = 0; // length of the subarray
for (int i = 0; i < nums.size(); i++) { // set the starting point of the subarray as i
sum = 0;
for (int j = i; j < nums.size(); j++) { // set the endpoint of the subarray as j
sum += nums[j];
if (sum >= s) { // once the sum exceeds s, update the result
subLength = j - i + 1; // take the subarray length
result = min(result, subLength);
break; // since we are looking for the shortest subarray that meets the conditions, we break once we find one
}
}
}
// if result hasn't been assigned, return 0, indicating no such subarray exists
return result == INT32_MAX ? 0 : result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
- Time Complexity: O(n^2)
- Space Complexity: O(1)
With the update of data on LeetCode, the brute force solution has timed out.
# Sliding Window
Next, we introduce another important method for array operations: Sliding Window.
The sliding window approach involves continuously adjusting the starting and ending positions of the subarray until we get the desired result.
In the brute force solution, a for loop represents the starting position of the sliding window and another for loop represents the ending position. This forms a continuous search through the intervals.
How can we use a single for loop to accomplish this operation?
First, think about whether a single for loop should represent the starting or ending position of the sliding window. If it represents only the starting position, how do we traverse the remaining ending positions?
This can easily lead to the trap of a brute force solution.
So if using a single for loop, the index must represent the ending position of the sliding window.
But how then do we move the starting position of the sliding window?
Let's walk through the example provided in the problem statement with s=7 and the array 2, 3, 1, 2, 4, 3 to understand the process:
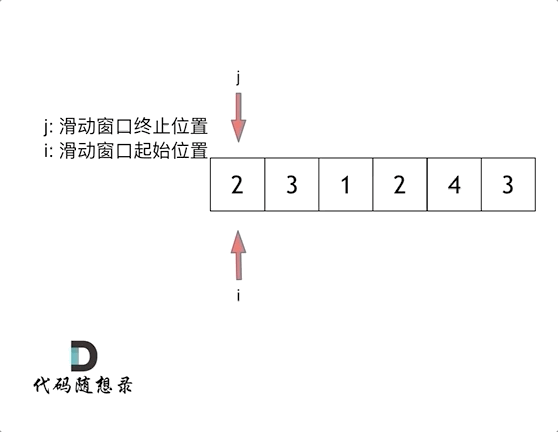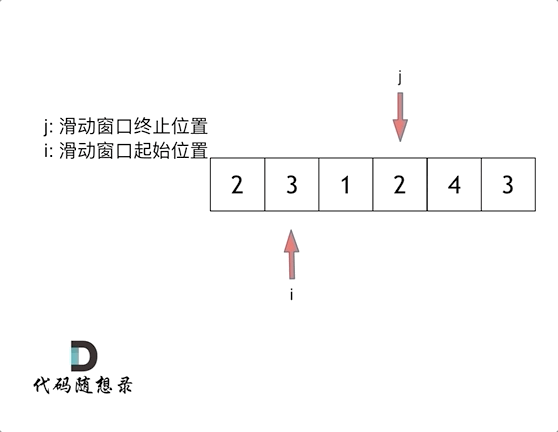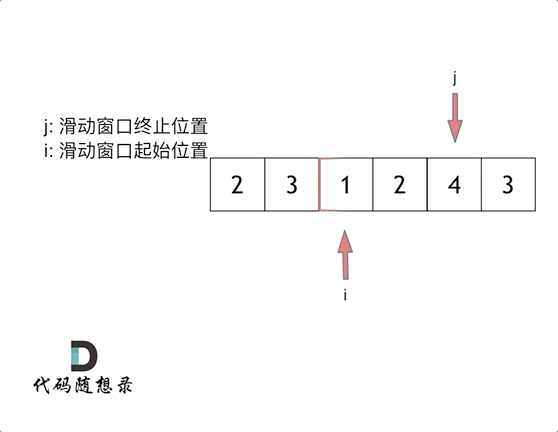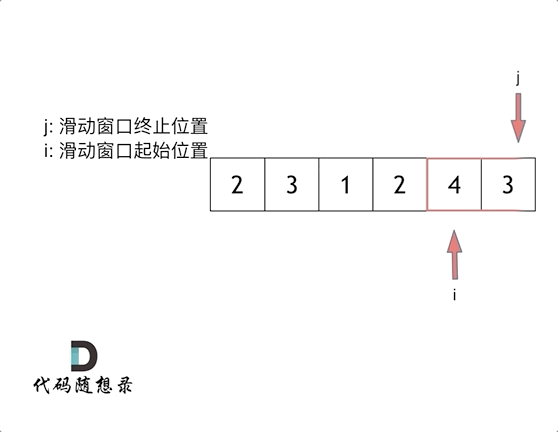
Ultimately, we find that [4, 3] is the shortest subarray that meets the requirement.
From the animation, you can see the sliding window can also be understood as a type of double-pointer approach! However, since this method resembles a window's movement, it's more appropriate to call it a sliding window.
In this problem, to implement a sliding window, primarily determine the following three points:
- What is within the window?
- How does the window's starting position move?
- How does the window's ending position move?
The window is the smallest contiguous subarray with a sum ≥ s.
The starting position of the window moves when the current window's sum exceeds s (i.e., it should be reduced).
The ending position of the window is just the index traversed by the array, i.e., the index in the for loop.
The key to solving this problem lies in how the starting position of the window moves, as shown in the diagram:
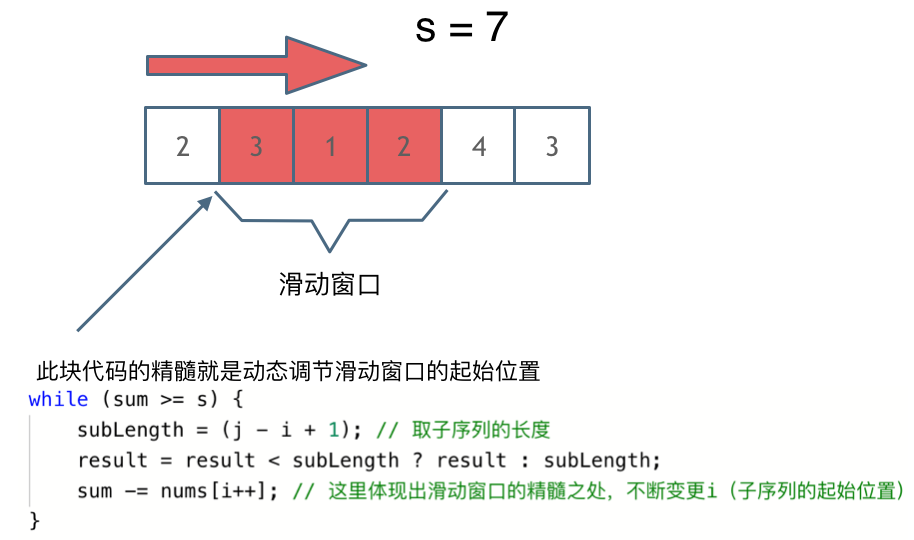
It can be seen that the highlight of the sliding window is in continuously adjusting the starting position according to the current subarray sum, thereby reducing the O(n^2) brute force solution to O(n).
Here's the C++ code:
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX;
int sum = 0; // sum of the sliding window
int i = 0; // start of the sliding window
int subLength = 0; // length of the sliding window
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
// Use while here to continuously update i (starting position) and check if the subarray meets the criteria
while (sum >= s) {
subLength = (j - i + 1); // take the length of the subarray
result = min(result, subLength);
sum -= nums[i++]; // This demonstrates the elegance of the sliding window approach, continuously adjusting i (starting position of the subarray)
}
}
// If result hasn't been assigned, return 0, indicating no such subarray exists
return result == INT32_MAX ? 0 : result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- Time Complexity: O(n)
- Space Complexity: O(1)
Some might wonder why the time complexity is O(n).
Don't assume it's O(n^2) just because there's a while within a for — mainly observe how many times each element is operated on. Every element is added to the sliding window once and removed once, so each element is operated on twice. Therefore, the time complexity is 2 × n, which is O(n).
# Related Problem Recommendations
# Implementations in Other Languages
# Java:
class Solution {
// Sliding window
public int minSubArrayLen(int s, int[] nums) {
int left = 0;
int sum = 0;
int result = Integer.MAX_VALUE;
for (int right = 0; right < nums.length; right++) {
sum += nums[right];
while (sum >= s) {
result = Math.min(result, right - left + 1);
sum -= nums[left++];
}
}
return result == Integer.MAX_VALUE ? 0 : result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Python:
# Version 1: Sliding Window
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
l = len(nums)
left = 0
right = 0
min_len = float('inf')
cur_sum = 0 # current accumulated value
while right < l:
cur_sum += nums[right]
while cur_sum >= s: # current accumulated value exceeds target
min_len = min(min_len, right - left + 1)
cur_sum -= nums[left]
left += 1
right += 1
return min_len if min_len != float('inf') else 0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Version 2: Brute Force
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
l = len(nums)
min_len = float('inf')
for i in range(l):
cur_sum = 0
for j in range(i, l):
cur_sum += nums[j]
if cur_sum >= s:
min_len = min(min_len, j - i + 1)
break
return min_len if min_len != float('inf') else 0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Go:
func minSubArrayLen(target int, nums []int) int {
i := 0
l := len(nums) // Length of the array
sum := 0 // Sum of the subarray
result := l + 1 // Initialize the length of the returned subarray to be l+1 to handle the case when there is no subarray that meets the criteria
for j := 0; j < l; j++ {
sum += nums[j]
while sum >= target {
subLength := j - i + 1
if subLength < result {
result = subLength
}
sum -= nums[i]
i++
}
}
if result == l+1 {
return 0
} else {
return result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# JavaScript:
var minSubArrayLen = function(target, nums) {
let start, end
start = end = 0
let sum = 0
let len = nums.length
let ans = Infinity
while(end < len){
sum += nums[end];
while (sum >= target) {
ans = Math.min(ans, end - start + 1);
sum -= nums[start];
start++;
}
end++;
}
return ans === Infinity ? 0 : ans
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# TypeScript:
function minSubArrayLen(target: number, nums: number[]): number {
let left: number = 0,
res: number = Infinity,
subLen: number = 0,
sum: number = 0;
for (let right: number = 0; right < nums.length; right++) {
sum += nums[right];
while (sum >= target) {
subLen = right - left + 1;
res = Math.min(res, subLen);
sum -= nums[left];
left++;
}
}
return res === Infinity ? 0 : res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Swift:
func minSubArrayLen(_ target: Int, _ nums: [Int]) -> Int {
var result = Int.max
var sum = 0
var starIndex = 0
for endIndex in 0..<nums.count {
sum += nums[endIndex]
while sum >= target {
result = min(result, endIndex - starIndex + 1)
sum -= nums[starIndex]
starIndex += 1
}
}
return result == Int.max ? 0 : result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Rust:
impl Solution {
pub fn min_sub_array_len(target: i32, nums: Vec<i32>) -> i32 {
let (mut result, mut subLength): (i32, i32) = (i32::MAX, 0);
let (mut sum, mut i) = (0, 0);
for (pos, val) in nums.iter().enumerate() {
sum += val;
while sum >= target {
subLength = (pos - i + 1) as i32;
if result > subLength {
result = subLength;
}
sum -= nums[i];
i += 1;
}
}
if result == i32::MAX {
return 0;
}
result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# PHP:
// Two Pointers - Sliding Window
class Solution {
/**
* @param Integer $target
* @param Integer[] $nums
* @return Integer
*/
function minSubArrayLen($target, $nums) {
if (count($nums) < 1) {
return 0;
}
$sum = 0;
$res = PHP_INT_MAX;
$left = 0;
for ($right = 0; $right < count($nums); $right++) {
$sum += $nums[$right];
while ($sum >= $target) {
$res = min($res, $right - $left + 1);
$sum -= $nums[$left];
$left++;
}
}
return $res == PHP_INT_MAX ? 0 : $res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Ruby:
def min_sub_array_len(target, nums)
res = Float::INFINITY # Infinity
i, sum = 0, 0
nums.length.times do |j|
sum += nums[j]
while sum >= target
res = [res, j - i + 1].min
sum -= nums[i]
i += 1
end
end
res == Float::INFINITY ? 0 : res
end
2
3
4
5
6
7
8
9
10
11
12
13
# C:
Brute force solution:
int minSubArrayLen(int target, int* nums, int numsSize){
// Initialize the minimum length as INT_MAX
int minLength = INT_MAX;
int sum;
int left, right;
for(left = 0; left < numsSize; ++left) {
// Reset sum to zero for each iteration to calculate the length of subarrays starting from the current position
sum = 0;
// Add elements to sum starting from left
for(right = left; right < numsSize; ++right) {
sum += nums[right];
// If adding the current element makes the sum exceed the target, update minLength
if(sum >= target) {
int subLength = right - left + 1;
minLength = min(minLength, subLength);
break;
}
}
}
// Return 0 if minLength remains INT_MAX, otherwise return minLength
return minLength == INT_MAX ? 0 : minLength;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Sliding window:
int minSubArrayLen(int target, int* nums, int numsSize){
// Initialize the minimum length as INT_MAX
int minLength = INT_MAX;
int sum = 0;
int left = 0, right = 0;
// Right boundary moves to the right
for(; right < numsSize; ++right) {
sum += nums[right];
// When sum is greater than or equal to target, save the length and shrink the left boundary
while(sum >= target) {
int subLength = right - left + 1;
minLength = min(minLength, subLength);
sum -= nums[left++];
}
}
// Return 0 if minLength remains INT_MAX, otherwise return minLength
return minLength == INT_MAX ? 0 : minLength;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Kotlin:
class Solution {
fun minSubArrayLen(target: Int, nums: IntArray): Int {
var start = 0
var end = 0
var ret = Int.MAX_VALUE
var count = 0
while (end < nums.size) {
count += nums[end]
while (count >= target) {
ret = if (ret > (end - start + 1)) end - start + 1 else ret
count -= nums[start++]
}
end++
}
return if (ret == Int.MAX_VALUE) 0 else ret
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Sliding window:
class Solution {
fun minSubArrayLen(target: Int, nums: IntArray): Int {
// Left and right boundaries
var left: Int = 0
var right: Int = 0
// sum keeps track of the total sum
var sum: Int = 0
// result keeps a fixed value, easy to determine if such an array exists
var result: Int = Int.MAX_VALUE
// subLenth keeps the length
var subLength = Int.MAX_VALUE
while (right < nums.size) {
// Start adding from the first element
sum += nums[right++]
// Check
while (sum >= target) {
var temp = right - left
// Compare with the last value each time to find the shortest length
subLength = if (subLength > temp) temp else subLength
// Reduce sum, move the left boundary right
sum -= nums[left++]
}
}
// Return 0 if subLength is the initial value, otherwise return subLength
return if(subLength == result) 0 else subLength
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Scala:
Sliding window:
object Solution {
def minSubArrayLen(target: Int, nums: Array[Int]): Int = {
var result = Int.MaxValue // Infinite
var left = 0 // slow pointer, move right when sum >= target
var sum = 0 // sum of the window
for (right <- 0 until nums.length) {
sum += nums(right)
while (sum >= target) {
result = math.min(result, right - left + 1) // generate new result
sum -= nums(left) // left pointer moves, reduce window sum
left += 1 // left pointer moves right
}
}
// Similar to a ternary operator, the return keyword can be discarded
if (result == Int.MaxValue) 0 else result
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Brute force:
object Solution {
def minSubArrayLen(target: Int, nums: Array[Int]): Int = {
import scala.util.control.Breaks
var res = Int.MaxValue
var subLength = 0
for (i <- 0 until nums.length) {
var sum = 0
Breaks.breakable(
for (j <- i until nums.length) {
sum += nums(j)
if (sum >= target) {
subLength = j - i + 1
res = math.min(subLength, res)
Breaks.break()
}
}
)
}
// Equivalent to a ternary operator
if (res == Int.MaxValue) 0 else res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C#:
public class Solution {
public int MinSubArrayLen(int s, int[] nums) {
int n = nums.Length;
int ans = int.MaxValue;
int start = 0, end = 0;
int sum = 0;
while (end < n) {
sum += nums[end];
while (sum >= s)
{
ans = Math.Min(ans, end - start + 1);
sum -= nums[start];
start++;
}
end++;
}
return ans == int.MaxValue ? 0 : ans;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
