# Array Summary
# Theoretical Basics of Arrays
Arrays are a fundamental data structure. In interviews, array-related questions are generally not challenging conceptually but mainly test your ability to control the code.
This means that while the idea might be simple, the implementation might not be straightforward.
First, you need to understand how arrays are stored in memory to truly grasp array-related interview questions.
Arrays are a collection of data of the same type stored in continuous memory spaces.
Arrays allow easy access to data at corresponding indexes via subscript indexing.
Let's take an example of a character array, as shown in the figure:
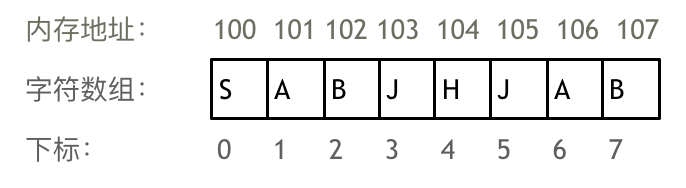
Two points to note:
- Array indices start from 0.
- The memory space of an array is continuous.
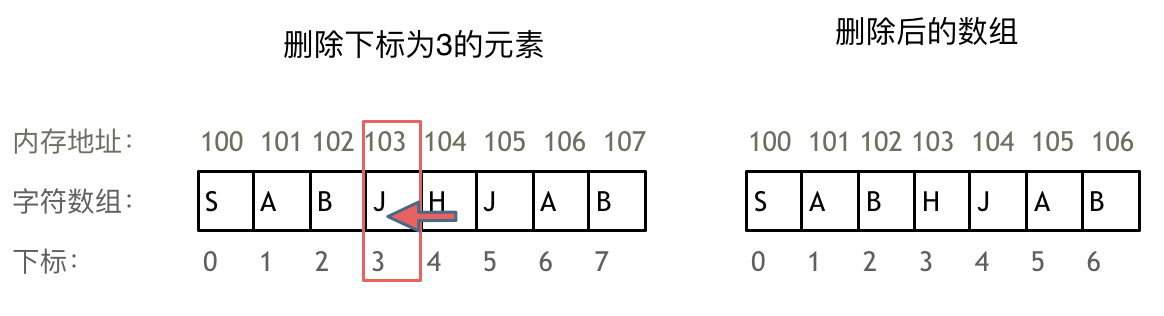
Precisely because an array's memory space is continuous, removing or adding elements often requires moving other elements' addresses.
For instance, if you delete the element at index 3, you must move all elements after index 3, as shown in the figure:
Also, if you are using C++, you should be aware of the difference between vectors and arrays. The underlying implementation of a vector is an array; strictly speaking, a vector is a container, not an array.
You cannot delete elements from an array; you can only overwrite them.
Now, let's look at two-dimensional arrays with a diagram, and you should understand how they work:
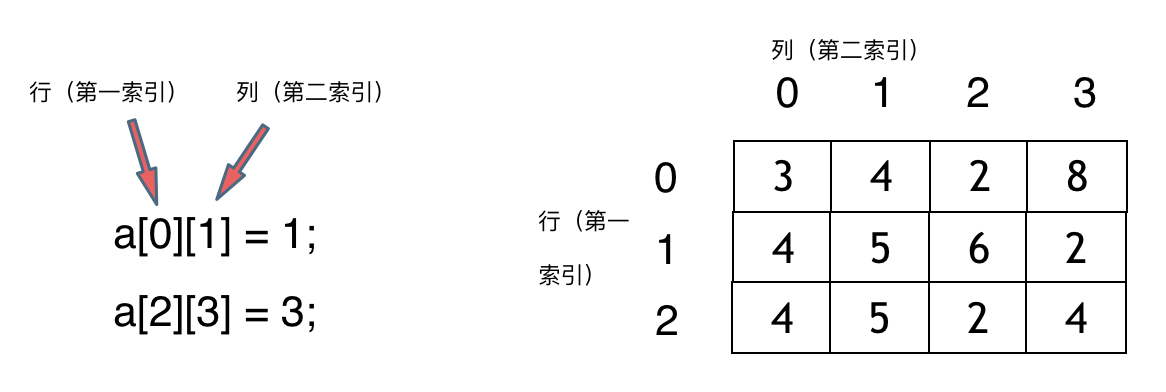
Is the memory space of a two-dimensional array continuous?
Let's take a Java example: int[][] rating = new int[3][4];. This two-dimensional array is not a 3*4 continuous address space in memory.
Looking at the diagram below should clarify that:
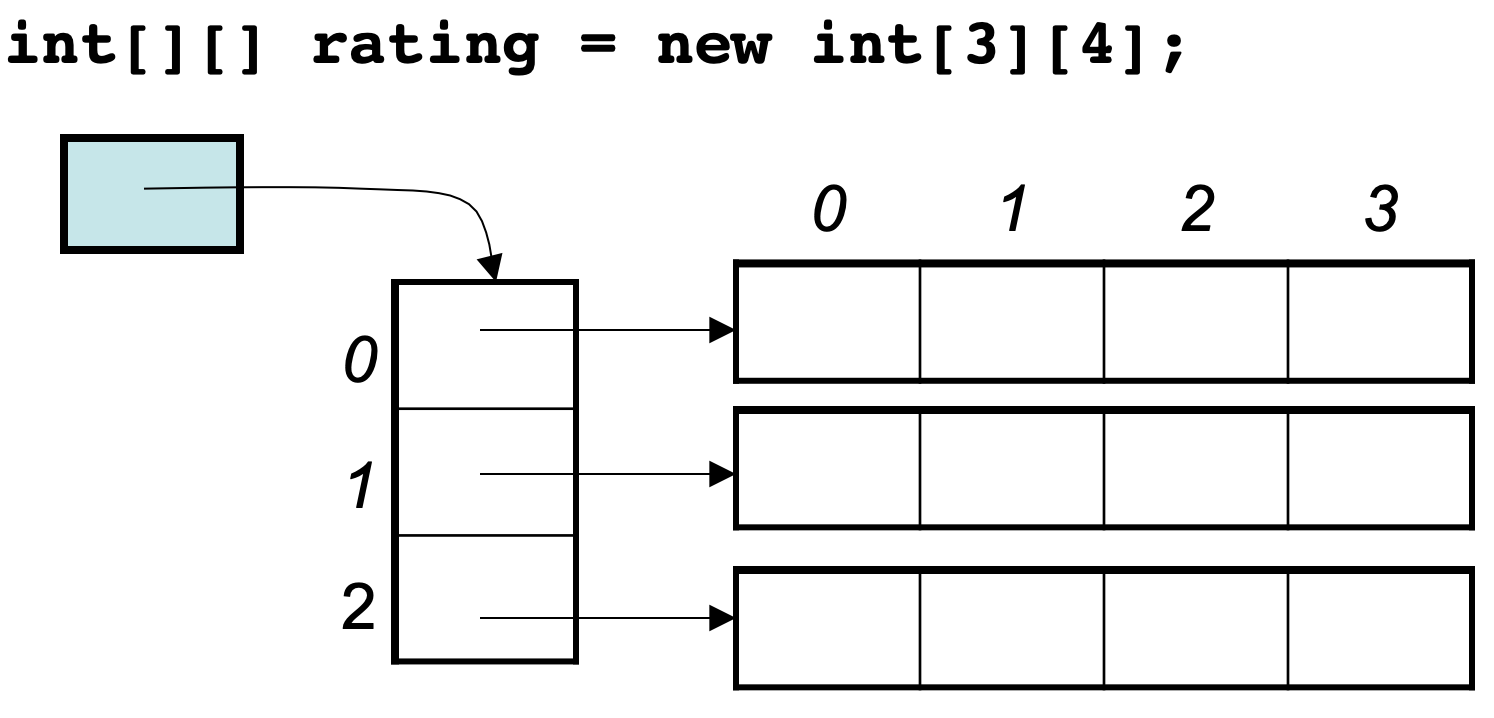
So, in Java, a two-dimensional array is not a 3*4 continuous address space in memory; instead, it is composed of several continuous address spaces.
# Classic Array Problems
In interviews, arrays are a fundamental data structure that will be tested.
In fact, array problems generally have simple ideas, but achieving high efficiency is not easy.
We have previously discussed four classic array problems, each representing a type, a specific idea.
# Binary Search
0704.Binary Search (opens new window)
This problem tests basic array operations. The idea is simple, but the pass rate is not very high among easy problems, so don't underestimate it.
You can use a brute force solution to solve this problem. If you aim for a more optimal algorithm, try using binary search to solve it.
- Brute force time complexity: O(n)
- Binary search time complexity: O(log n)
In this problem, we discussed the loop invariant principle. Only by adhering to the definition of intervals within loops can you clearly grasp various details in the loops.
Binary search is a common question in algorithm interviews. It is recommended to practice hand-coding binary search through this problem.
# Two-Pointer Technique
Two-pointer technique (fast and slow pointers): Using a fast pointer and a slow pointer in a single for loop to accomplish the work of two for loops.
- Brute force time complexity: O(n^2)
- Two-pointer time complexity: O(n)
This problem has puzzled many, who get caught up in why elements cannot be deleted from an array. This mainly stems from two points:
- Arrays in memory are continuous address spaces. Single elements cannot be released; if you release them, you release everything (memory stack space is reclaimed when the program runs).
- It's crucial to understand the difference between vectors and arrays in C++, with vectors being more user-friendly due to encapsulation on top of arrays.
The two-pointer technique (fast and slow pointers) is very common in operations on arrays and linked lists. Many interview questions concerning array and linked list operations use the two-pointer technique.
# Sliding Window
This problem introduces another important concept in array manipulation: the sliding window.
- Brute force time complexity: O(n^2)
- Sliding window time complexity: O(n)
In this problem, the main objective is to understand how the sliding window adjusts its starting position to dynamically update its size and derive the minimum length that meets the condition.
The brilliance of the sliding window lies in adjusting the start position of the subsequence based on the current sum, reducing the time complexity from O(n^2) to O(n).
If you've never encountered this method, it might be difficult to think of similar solution styles. The sliding window technique is indeed clever.
# Simulating Behavior
Simulation problems are common in arrays, involving no particular algorithm but rather merely simulating behavior, which greatly tests your ability to control code.
In this problem, we once again introduced the loop invariant principle, which is also an important principle in coding.
You might have encountered situations where boundary adjustments are overwhelming, with barriers and patches everywhere, ultimately resulting in a convoluted, redundant code that lacks structure. In reality, the ultimate solutions to problems are often concise or principled. You can appreciate this in this problem.
# Prefix Sum
Subsequent questions will be supplemented in "Code Thoughts"
The prefix sum concept is straightforward but very practical. If you've never encountered this method, it might be difficult to think of this dimension for a solution, making it a great question to broaden your problem-solving approach without high difficulty.
# Conclusion
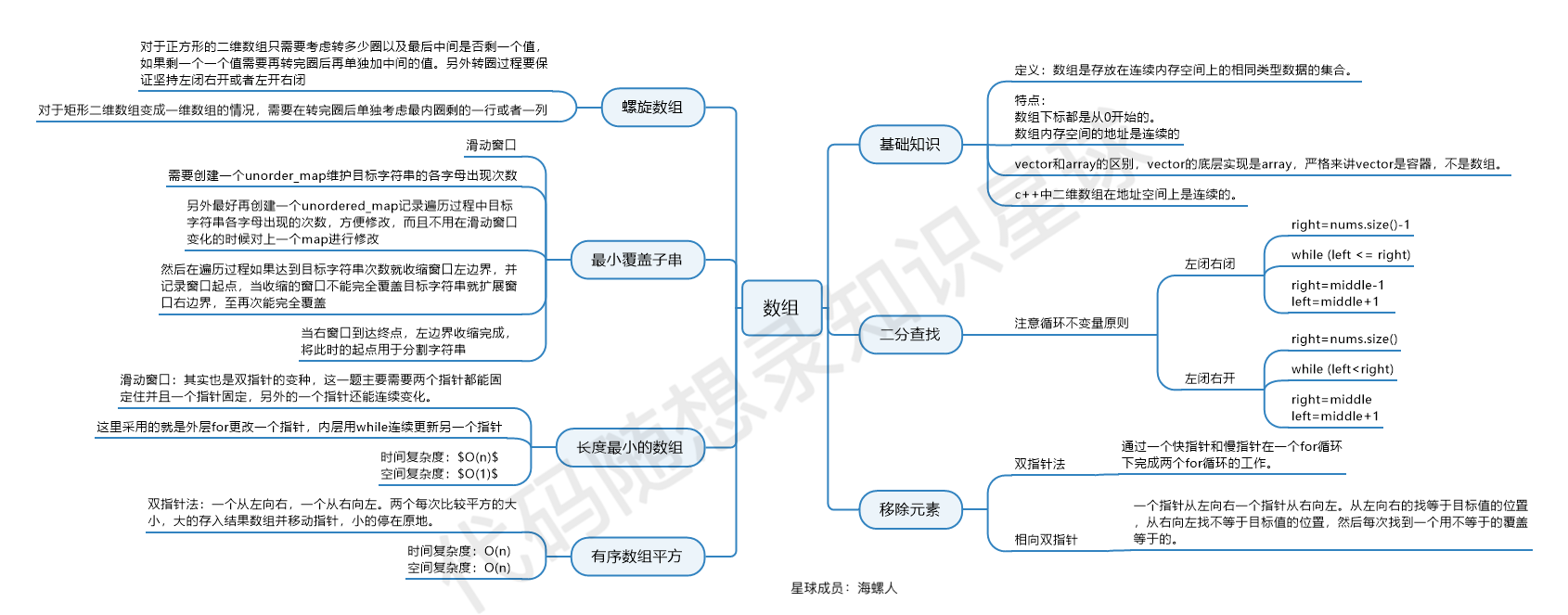
This diagram was created by Hai Luo Ren (opens new window), a member of Keet Coder (opens new window), and provides an excellent summary to share with everyone.
From binary search to two-pointer, from sliding window to spiral matrix, if you seriously solve the daily recommended problems from "Code Thoughts", you'll certainly gain a lot.
Even if you have done the recommended questions before, re-reading the articles will help you extract the essence of the problem-solving methods.
