Complete Knapsack - One-Dimensional Array

There is no direct problem for this on LeetCode. You can practice it on Kamacoder Problem 52 (opens new window).

Thought Process

In this section, we will not analyze the "five steps" as the core content has already been explained in previous discussions about the 0/1 Knapsack with a two-dimensional array, the 0/1 Knapsack with a one-dimensional array, and the Complete Knapsack with a two-dimensional array.

In the previous article, we just discussed the implementation of the Complete Knapsack problem using a two-dimensional DP array:

for (int i = 1; i < n; i++) { // Traverse items
    for(int j = 0; j <= bagWeight; j++) { // Traverse bag capacity
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
    }
}

Compression into a one-dimensional DP array essentially means copying the previous layer to the current layer.

Copy the previous layer dp[i-1] to the current layer dp[i], then the recurrence relation changes from dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]) to dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]).

Some of you might think, won’t the values of dp[i - 1][j] get overwritten by the values of dp[i][j]?

No, they won’t, because the current layer dp[i][j] is empty and hasn't been computed yet.

So it evolves into dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]) and then we compress it into a one-dimensional DP array, removing the dimension of layer i.

That is: dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

Next, we focus on the traversal order.

If you have read the following articles:

• Knapsack Theory 01 Knapsack-1 (opens new window)
• Knapsack Theory 01 Knapsack-2 (opens new window)

You'll know that in the 0/1 Knapsack problem, the order of the two nested for loops in a two-dimensional DP array can be reversed. However, in a one-dimensional DP array, the for loops must first iterate over the items and then the knapsack capacity.

In the Complete Knapsack problem, the order of the two nested for loops does not matter for a one-dimensional DP array!

This is because dp[j] is computed based on the dp[j]'s for indices less than j. As long as those indices have already been calculated, you’re good.

With items as the outer loop and bag capacity as the inner loop, the state looks like this:

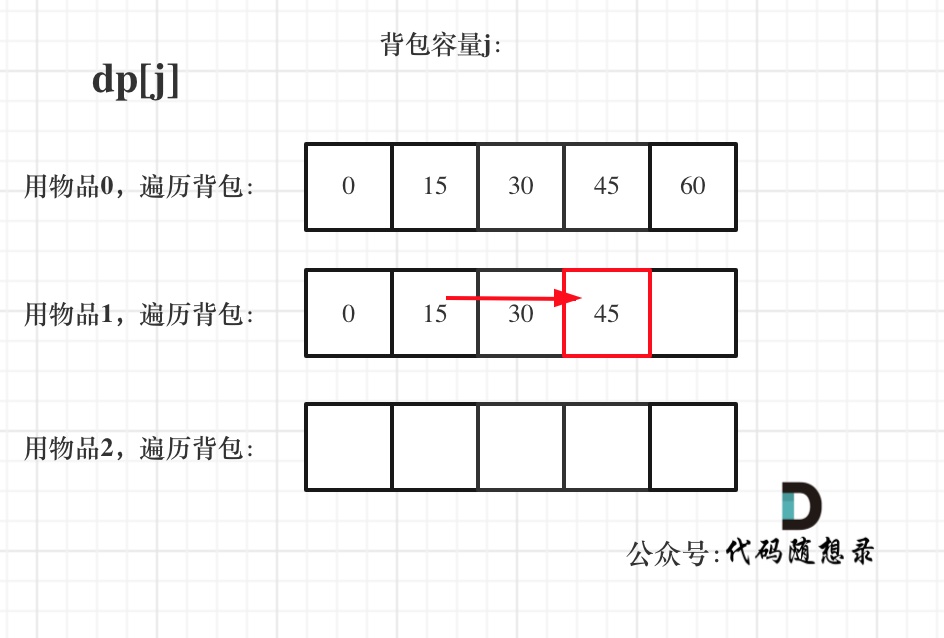
With bag capacity as the outer loop and items as the inner loop, the state looks like this:

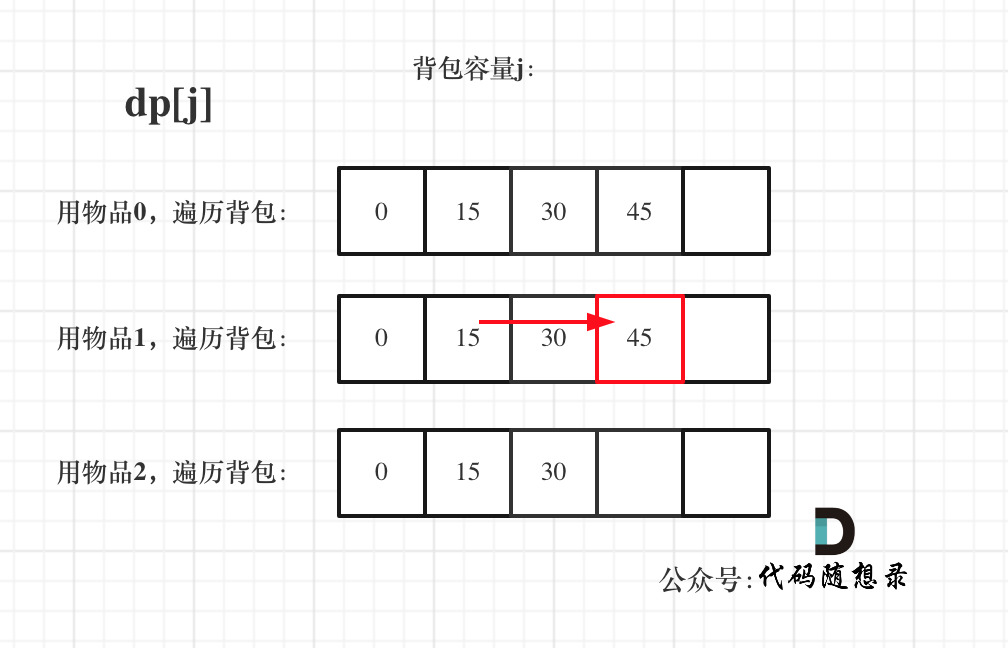
Looking at these two diagrams, you'll understand that in the Complete Knapsack, the order of the for loops does not affect the computation of the needed value for dp[j] (which is derived from the previously calculated dp[j]'s for indices less than j).

First iterate over the bag capacity then the items, code is as follows:

for(int j = 0; j <= bagWeight; j++) { // Traverse bag capacity
    for(int i = 0; i < weight.size(); i++) { // Traverse items
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}

First iterate over the items then the bag capacity:

for(int i = 0; i < weight.size(); i++) { // Traverse items
    for(int j = 0; j <= bagWeight; j++) { // Traverse bag capacity
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

Below is the full code:

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int N, bagWeight;
    cin >> N >> bagWeight;
    vector<int> weight(N, 0);
    vector<int> value(N, 0);
    for (int i = 0; i < N; i++) {
        int w;
        int v;
        cin >> w >> v;
        weight[i] = w;
        value[i] = v;
    }

    vector<int> dp(bagWeight + 1, 0);
    for(int j = 0; j <= bagWeight; j++) { // Traverse bag capacity
        for(int i = 0; i < weight.size(); i++) { // Traverse items
            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;

    return 0;
}

Summary

Keen-eyed readers may have noticed that I continually refer to the pure Complete Knapsack problem, indicating its for loop order can be switched freely!

But if there’s a slight change in the problem, this change will reflect in the order of traversal.

For example, if the question asks how many ways to fill the knapsack, the order of the two nested for loops will make a significant difference. And most problems on LeetCode belong to this slightly varied type.

I will explain this difference in detail in subsequent sections using specific LeetCode problems, as explaining pure theory without real data might confuse a lot of readers.

But don’t worry, the next part is coming soon!

Finally, this revelation could serve as a potential interview question: implement a pure Complete Knapsack problem first using a two-dimensional DP array, then with a one-dimensional DP array, and lastly ask whether the order of two for loops can be reversed, and why?

This seemingly simple Complete Knapsack question might stump many candidates.

Other Language Versions

Java:

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int bagWeight = scanner.nextInt();

        int[] weight = new int[N];
        int[] value = new int[N];
        for (int i = 0; i < N; i++) {
            weight[i] = scanner.nextInt();
            value[i] = scanner.nextInt();
        }

        int[] dp = new int[bagWeight + 1];

        for (int j = 0; j <= bagWeight; j++) { // Traverse bag capacity
            for (int i = 0; i < weight.length; i++) { // Traverse items
                if (j >= weight[i]) {
                    dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
                }
            }
        }

        System.out.println(dp[bagWeight]);
        scanner.close();
    }
}

Python:

def complete_knapsack(N, bag_weight, weight, value):
    dp = [0] * (bag_weight + 1)

    for j in range(bag_weight + 1):  # Traverse bag capacity
        for i in range(len(weight)):  # Traverse items
            if j >= weight[i]:
                dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

    return dp[bag_weight]

# Input
N, bag_weight = map(int, input().split())
weight = []
value = []
for _ in range(N):
    w, v = map(int, input().split())
    weight.append(w)
    value.append(v)

# Output result
print(complete_knapsack(N, bag_weight, weight, value))

Go:

Javascript: