797. All Paths From Source to Target

LeetCode Problem Link (opens new window)

Given a directed acyclic graph (DAG) with n nodes, find all possible paths from node 0 to node n-1 and return them in any order.

graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

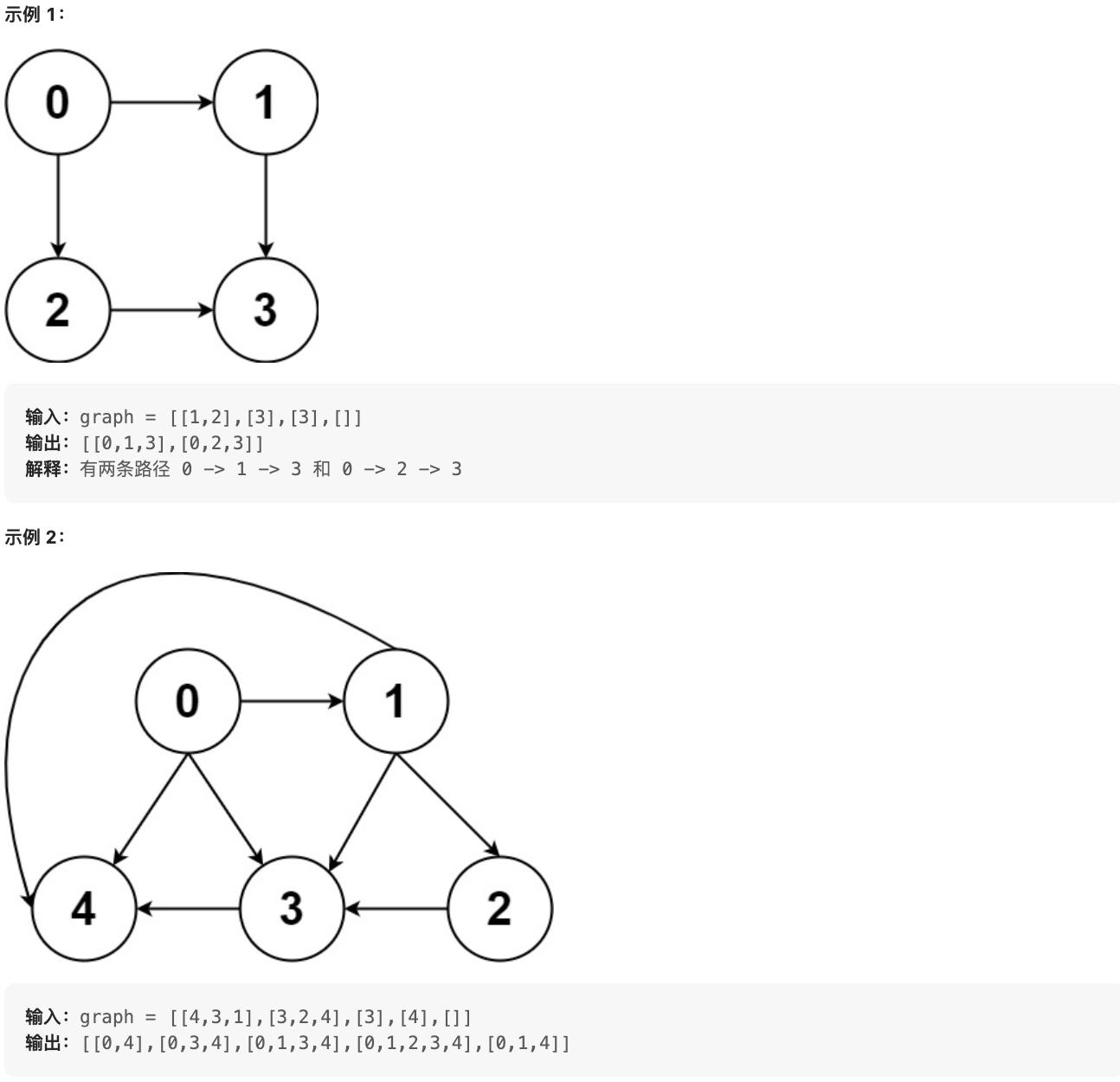
Constraints:

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i (i.e., there are no self loops)
• All elements of graph[i] are distinct
• The input graph is guaranteed to be a directed acyclic graph (DAG)

Approach

This problem is a straightforward depth-first search (DFS) problem.

If you are not familiar with DFS, you might want to start here: Depth First Search Basics (opens new window)

I have summarized the three-step approach for DFS. If you are familiar with the three-step approach for recursion in binary trees or backtracking, this will look familiar.

One might wonder, what is the difference between DFS, binary trees, and backtracking? When should I use DFS and when backtracking?

As I mentioned in the Binary Tree Basics (opens new window), binary tree traversals like pre-order, in-order, and post-order are essentially DFS applied to tree structures.

As for backtracking, backtracking is essentially DFS but more specifically defined.

So, someone might ask: can I call backtracking as DFS?

Theoretically, yes, but it's like calling a binary tree just a data structure instead of its specific name. There's nothing wrong with it, but it's more precise to use the specific name when possible. That's why backtracking can be considered a subset of DFS.

Now, let's use the three-step approach to analyze the problem:

1. Define the recursive function and its parameters

   First, our dfs function must store a graph for traversal, and keep track of the current node, denoted as x.

   As for the single path and path collection, they can be stored in global variables. The code would look something like this:

   vector<vector<int>> result; // Collects paths that meet the criteria
   vector<int> path; // Path from node 0 to the target
   // x: currently visited node
   // graph: stores the current graph
   void dfs (vector<vector<int>>& graph, int x);
   

2. Define the termination condition

   When do we find a complete path?

   When we are currently visiting the last node, we have found a path from the source to the target.

   The currently visited node is x, and the last node is graph.size() - 1 (because the problem asks us to find all paths from node 0 to node n-1).

   Thus, when x equals graph.size() - 1, we have found a valid path. The code is as follows:

   // We need to find paths from node 0 to node n-1, which is graph.size() - 1
   if (x == graph.size() - 1) { // Found a valid path
       result.push_back(path); // Collect the valid path
       return;
   }
   

3. Process the path from the current node to subsequent nodes

   Next, we need to traverse from the current node x to its next connected nodes.

   We first find out what nodes are connected to x by traversing:

   for (int i = 0; i < graph[x].size(); i++) { // Traverse all nodes connected to node x
   

   We then add the chosen node connected to x to the single path:

   path.push_back(graph[x][i]); // Add the traversed node to the path
   

   Some might wonder how we find nodes connected to x. For example, if x is currently node 0, the process looks like this:

   

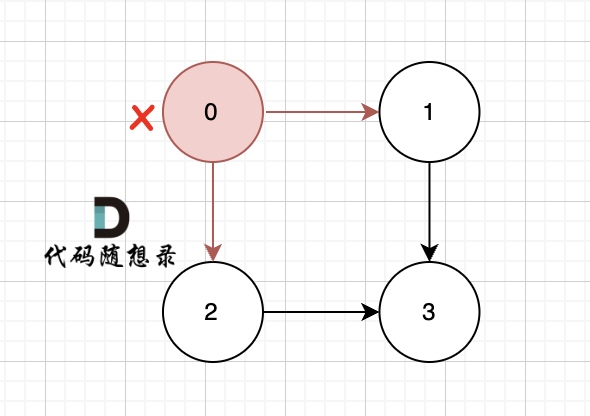
   The nodes graph[x][i] are those connected to x; the node currently visited is graph[x][i].

   Go to the next layer of recursion:

   dfs(graph, graph[x][i]); // Enter the next level of recursion
   

   Finally, undo the current addition of the node in the backtracking step. The entire code for this process is:

   for (int i = 0; i < graph[x].size(); i++) { // Traverse all nodes connected to node x
       path.push_back(graph[x][i]); // Add the traversed node to the path
       dfs(graph, graph[x][i]); // Enter the next level of recursion
       path.pop_back(); // Backtrack, undo the addition of this node
   }
   

Here's the complete code for this problem:

class Solution {
private:
    vector<vector<int>> result; // Collects valid paths
    vector<int> path; // Path from the start to the target node
    // x: current node
    // graph: current graph
    void dfs (vector<vector<int>>& graph, int x) {
        if (x == graph.size() - 1) { // Find a valid path
            result.push_back(path);
            return;
        }
        for (int i = 0; i < graph[x].size(); i++) { // Iterate over nodes connected to x
            path.push_back(graph[x][i]); // Add to the path
            dfs(graph, graph[x][i]); // Recurse
            path.pop_back(); // Backtrack
        }
    }
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        path.push_back(0); // Start from node 0
        dfs(graph, 0); // Begin traversal
        return result;
    }
};

Summary

This problem is a basic DFS template question. Directed graph path problems are well-suited for DFS, though BFS could be used but would be more complex due to path tracking considerations.

DFS and BFS are both applicable for problems similar to the "Island" series, which essentially involves traversal and marking, making either approach valid.

The BFS theoretical basis will be discussed in a future article, so stay tuned!

Other Language Versions

Java

// Depth-first search
class Solution {
    List<List<Integer>> ans; // Holds paths that meet the criteria
    List<Integer> cnt; // Stores nodes during dfs

    public void dfs(int[][] graph, int node) {
        if (node == graph.length - 1) { // If current node is n - 1, save the path
            ans.add(new ArrayList<>(cnt));
            return;
        }
        for (int index = 0; index < graph[node].length; index++) {
            int nextNode = graph[node][index];
            cnt.add(nextNode);
            dfs(graph, nextNode);
            cnt.remove(cnt.size() - 1); // Backtracking
        }
    }

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        ans = new ArrayList<>();
        cnt = new ArrayList<>();
        cnt.add(0); // Note: Node 0 needs to be added to cnt
        dfs(graph, 0);
        return ans;
    }
}

Python

class Solution:
    def __init__(self):
        self.result = []
        self.path = [0]

    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        if not graph: return []

        self.dfs(graph, 0)
        return self.result
    
    def dfs(self, graph, root: int):
        if root == len(graph) - 1: # Found a valid path
            # ***Python list is mutable***
            # ***Deep Copy is necessary in backtracking***
            self.result.append(self.path[:]) 
            return
        
        for node in graph[root]: # Traverse all subsequent nodes of n
            self.path.append(node)
            self.dfs(graph, node)
            self.path.pop() # Backtracking

JavaScript

var allPathsSourceTarget = function(graph) {
    let res=[],path=[]

    function dfs(graph,start){
        if(start===graph.length-1){
            res.push([...path])
            return;
        }
        for(let i=0;i<graph[start].length;i++){
            path.push(graph[start][i])
            dfs(graph,graph[start][i])
            path.pop()
        }
    }
    path.push(0)
    dfs(graph,0)
    return res
};

Go

func allPathsSourceTarget(graph [][]int) [][]int {
    result := make([][]int, 0)

    var dfs func(path []int, step int)
    dfs = func(path []int, step int){
        // Traverse from 0 to length-1
        if step == len(graph) - 1{
            tmp := make([]int, len(path))
            copy(tmp, path)
            result = append(result, tmp)
            return 
        }

        for i := 0; i < len(graph[step]); i++{
            next := append(path, graph[step][i])
            dfs(next, graph[step][i])
        }
    }
    // Start from 0, initially push 0
    dfs([]int{0}, 0)
    return result 
}

Rust

impl Solution {
    pub fn all_paths_source_target(graph: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let (mut res, mut path) = (vec![], vec![0]);
        Self::dfs(&graph, &mut path, &mut res, 0);
        res
    }

    pub fn dfs(graph: &Vec<Vec<i32>>, path: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, node: usize) {
        if node == graph.len() - 1 {
            res.push(path.clone());
            return;
        }
        for &v in &graph[node] {
            path.push(v);
            Self::dfs(graph, path, res, v as usize);
            path.pop();
        }
    }
}