347. Top K Frequent Elements

LeetCode Problem Link (opens new window)

Given a non-empty array of integers, return the k most frequent elements.

Example 1:

• Input: nums = [1,1,1,2,2,3], k = 2
• Output: [1,2]

Example 2:

• Input: nums = [1], k = 1
• Output: [1]

Constraints:

• You may assume k is always valid, 1 ≤ k ≤ number of unique elements in the array.
• Your algorithm's time complexity must be better than O(n log n), where n is the array's size.
• It is guaranteed that the answer is unique, in other words, the set of the k most frequent elements is unique.
• You can return the answer in any order.

Thoughts

This problem mainly involves three sections:

1. Count the frequency of elements
2. Sort the frequency
3. Identify the top k frequent elements

First, count the frequency of elements. This type of problem can be solved using a map for statistics.

Next is sorting the frequency. Here we can use a container adapter known as a priority queue.

What exactly is a priority queue?

Essentially, it's a heap in the guise of a queue, as the priority queue only presents interfaces for taking elements from the head and adding elements to the tail, with no other ways to take elements, it looks like a queue.

Moreover, elements inside the priority queue are automatically arranged according to their weight. So how is it ordered?

By default, priority_queue utilizes a max-heap to complete the sorting of elements, this max-heap is a complete binary tree shown as a vector.

What is a heap?

A heap is a complete binary tree where each node's value is no smaller (or no greater) than the values of its children. If the parent's node value is greater than or equal to its children it's a max-heap, if it's smaller or equal then it's a min-heap.

Thus, people often refer to a max-heap (heap head with the maximum element), and a min-heap (heap head with the minimum element). If you're not interested in implementing it yourself, directly using priority_queue is perfectly fine, as its underlying implementation is the same, a min-heap sorts from smallest to largest, and a max-heap from largest to smallest.

In this problem, we use the priority queue to sort a subset of the frequencies.

Why not use quicksort? Using quicksort requires transforming the map into a vector structure, and sorting the entire array. However, in this scenario, we only need to maintain a sorted sequence of k elements, so the priority queue is optimal.

Now, consider whether to use a min-heap or a max-heap?

Some may think, the problem asks for the top k frequent elements, so go for a max-heap.

Then there's a problem, defining a max-heap of size k, during updates every time you remove elements you pop out the maximum element, so how can you keep the top k frequent elements?

Moreover, using a max-heap will require sorting all elements, can we achieve sorting with just k elements?

So a min-heap should be used because to find the top k maximum elements means only sorting the smallest element out each time, leaving the top k largest elements accumulated in the min-heap.

The process of finding the top k largest elements is illustrated: (The frequencies illustrated have three so exactly form a min-heap of size 3, if there were more frequencies the min-heap would be used for scanning)

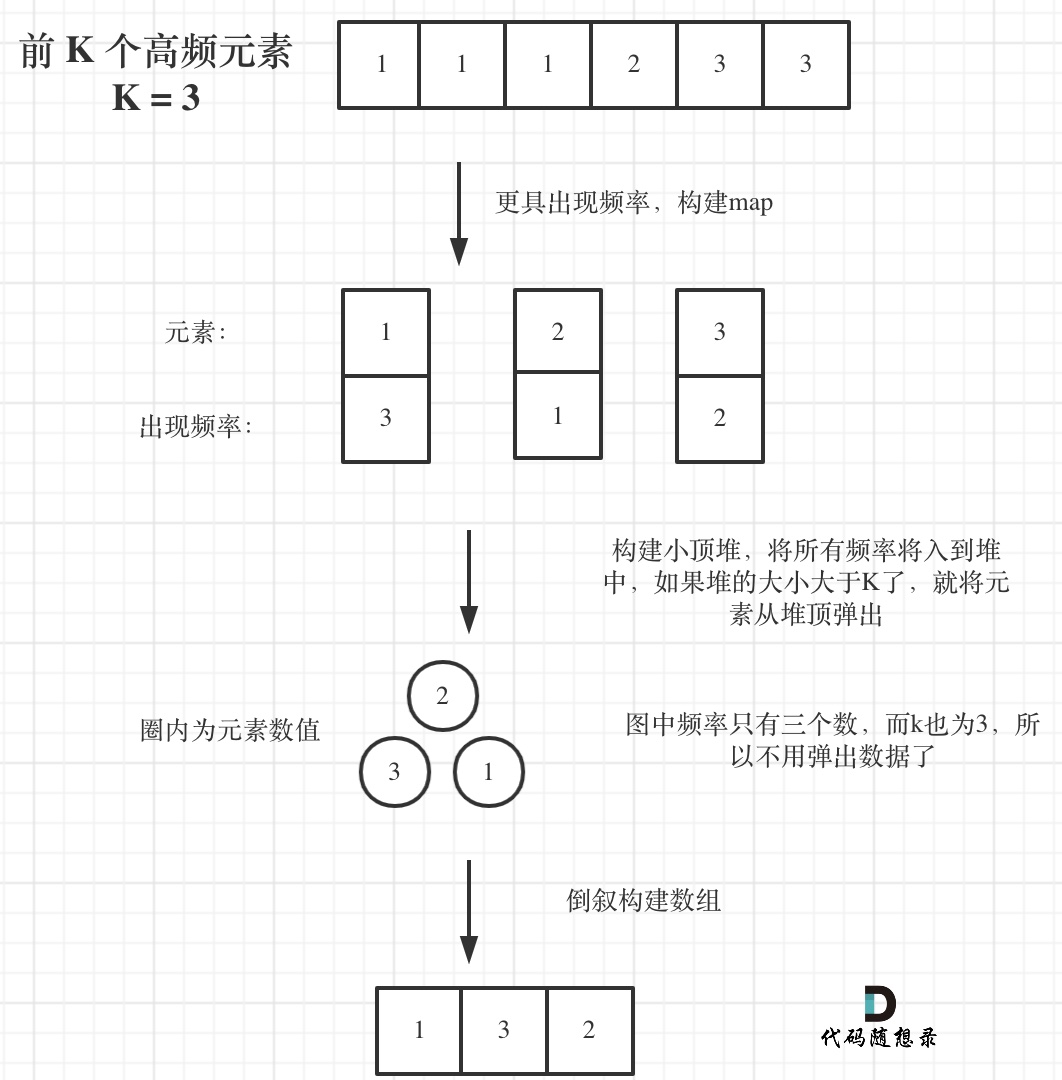
Let's look at the C++ code:

class Solution {
public:
    // Min-heap
    class mycomparison {
    public:
        bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
            return lhs.second > rhs.second;
        }
    };
    vector<int> topKFrequent(vector<int>& nums, int k) {
        // Count the occurrence frequency of elements
        unordered_map<int, int> map; // map<nums[i], corresponding count>
        for (int i = 0; i < nums.size(); i++) {
            map[nums[i]]++;
        }

        // Sort the frequencies
        // Define a min-heap with size k
        priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;

        // Use a fixed size k min-heap to scan through all number frequencies
        for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++) {
            pri_que.push(*it);
            if (pri_que.size() > k) { // If heap size is larger than k, pop, to keep heap size at k
                pri_que.pop();
            }
        }

        // Find the top K frequent elements, because min-heap pops the smallest first, results are output in reverse order to array
        vector<int> result(k);
        for (int i = k - 1; i >= 0; i--) {
            result[i] = pri_que.top().first;
            pri_que.pop();
        }
        return result;
    }
};

• Time Complexity: O(n log k)
• Space Complexity: O(n)

Extension

Many find it confusing why the comparison operation results in these heap constructions, why specifying left > right builds a min-heap, but conversely constructs a max-heap.

Indeed, for instance, writing the cmp function for quicksort where return left > right sorts from largest to smallest, while return left < right sorts from smallest to largest.

The definition for priority queues is precisely reversed. This may be related to the implementation details of the priority queue (which I haven't studied closely), presumably due to the underlying implementation setting the priority queue's head points backward, while the tail points to the front!

Solutions in Other Languages

Java:

/*Comparator interface explanation:
 * Returning a negative number: the first parameter appears first;
 * Returning a positive number: the second parameter appears first.
 * For queue: appearing first means closer to the front.
 * For heaps (implemented using PriorityQueue):
 *   - Sorted from smallest to largest is a min-heap.
 *   - Sorted from largest to smallest is a max-heap.
 */
class Solution {
    // Solution 1: Based on a max-heap.
    public int[] topKFrequent1(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>(); // Value is the count of occurrences of the key.
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        // PriorityQueue storing tuples (num, cnt). cnt denotes the frequency of num in the array.
        // Frequency sorted from highest at the front (similarly to max-heap).
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair2[1] - pair1[1]);
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) { // Max-heap requires sorting all elements.
            pq.add(new int[]{entry.getKey(), entry.getValue()});
        }
        int[] ans = new int[k];
        for (int i = 0; i < k; i++) { // Poll the top k high frequency elements.
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
    // Solution 2: Based on a min-heap.
    public int[] topKFrequent2(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        // PriorityQueue storing tuples (num, cnt). cnt denotes the frequency of num in the array.
        // Frequency sorted from lowest at the front (similarly to min-heap).
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair1[1] - pair2[1]);
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) { // Min-heap requires sorting k elements only.
            if (pq.size() < k) {
                pq.add(new int[]{entry.getKey(), entry.getValue()});
            } else {
                if (entry.getValue() > pq.peek()[1]) { // Current frequency is greater than heap root.
                    pq.poll(); // Pop top (smallest frequency).
                    pq.add(new int[]{entry.getKey(), entry.getValue()});
                }
            }
        }
        int[] ans = new int[k];
        for (int i = k - 1; i >= 0; i--) { // Poll the k highest frequency elements.
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
}

Simplified version:

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[1] - o2[1]);
        int[] res = new int[k];
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) map.put(num, map.getOrDefault(num, 0) + 1);
        for (var x : map.entrySet()) {
            int[] tmp = new int[2];
            tmp[0] = x.getKey();
            tmp[1] = x.getValue();
            pq.offer(tmp);
            if (pq.size() > k) {
                pq.poll();
            }
        }
        for (int i = 0; i < k; i++) {
            res[i] = pq.poll()[0];
        }
        return res;
    }
}

Python:

Solution 1:

# Time complexity: O(nlogk)
# Space complexity: O(n)
import heapq
class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        # Count the occurrence frequency of elements
        map_ = {} # A dictionary of nums[i] with corresponding count
        for i in range(len(nums)):
            map_[nums[i]] = map_.get(nums[i], 0) + 1
        
        # Sort the frequencies
        # Define a min-heap of size k
        pri_que = [] # Min-heap
        
        # Scan using a k-sized min-heap
        for key, freq in map_.items():
            heapq.heappush(pri_que, (freq, key))
            if len(pri_que) > k: # All the times when more than k items
                heapq.heappop(pri_que)
        
        # Find the Top K frequent elements
        result = [0] * k
        for i in range(k-1, -1, -1):
            result[i] = heapq.heappop(pri_que)[1]
        return result

Solution 2:

class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        time_dict = defaultdict(int)
        for num in nums:
            time_dict[num] += 1
        index_dict = defaultdict(list)
        for key in time_dict:
            index_dict[time_dict[key]].append(key)
        key = list(index_dict.keys())
        key.sort()
        result = []
        cnt = 0
        while key and cnt != k:
            result += index_dict[key[-1]]
            cnt += len(index_dict[key[-1]])
            key.pop()

        return result[0: k]

Go:

//Approach 1: Min-heap
func topKFrequent(nums []int, k int) []int {
    map_num:=map[int]int{}
    for _,item:=range nums{
        map_num[item]++
    }
    h:=&IHeap{}
    heap.Init(h)
    for key,value:=range map_num{
        heap.Push(h,[2]int{key,value})
        if h.Len()>k{
            heap.Pop(h)
        }
    }
    res:=make([]int,k)
    for i:=0;i<k;i++{
        res[k-i-1]=heap.Pop(h).([2]int)[0]
    }
    return res
}

// Build a min-heap
type IHeap [][2]int

func (h IHeap) Len()int {
    return len(h)
}

func (h IHeap) Less (i,j int) bool {
    return h[i][1]<h[j][1]
}

func (h IHeap) Swap(i,j int) {
    h[i],h[j]=h[j],h[i]
}

func (h *IHeap) Push(x interface{}){
    *h=append(*h,x.([2]int))
}
func (h *IHeap) Pop() interface{}{
    old:=*h
    n:=len(old)
    x:=old[n-1]
    *h=old[0:n-1]
    return x
}


//Approach 2: Using O(nlogn) sorting
func topKFrequent(nums []int, k int) []int {
    ans:=[]int{}
    map_num:=map[int]int{}
    for _,item:=range nums {
        map_num[item]++
    }
    for key,_:=range map_num{
        ans=append(ans,key)
    }
    sort.Slice(ans,func (a,b int)bool{
        return map_num[ans[a]]>map_num[ans[b]]
    })
    return ans[:k]
}

JavaScript:

Solution 1: LeetCode provides a library for priority queues, refer to @datastructures-js/priority-queue (opens new window).

var topKFrequent = function(nums, k) {
  const map = new Map();
  const res = [];
  for (const num of nums) {
    map.set(num, (map.get(num) || 0) + 1);
  }
  const heap = new PriorityQueue({
    compare: (a, b) => a.value - b.value
  })
  for (const [key, value] of map) {
    heap.enqueue({ key, value });
    if (heap.size() > k) heap.dequeue();
  }
  while (heap.size()) res.push(heap.dequeue().key);
  return res;
};

Solution 2: Self-written priority queue implementation

// JavaScript doesn't have heap; we need to construct it ourselves
class Heap {
    constructor(compareFn) {
        this.compareFn = compareFn;
        this.queue = [];
    }

    push(item) {
        this.queue.push(item);

        let index = this.size() - 1; 
        let parent = Math.floor((index - 1) / 2); 

        while (parent >= 0 && this.compare(parent, index) > 0) { 
            [this.queue[index], this.queue[parent]] = [this.queue[parent], this.queue[index]];

            index = parent;
            parent = Math.floor((index - 1) / 2);
        }
    }

    pop() {
        if (this.size() <= 1) {
            return this.queue.pop()
        }

        const out = this.queue[0];
        this.queue[0] = this.queue.pop();

        let index = 0; 
        let left = 1;
        let searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;

        while (this.compare(index, searchChild) > 0) {
            [this.queue[index], this.queue[searchChild]] = [this.queue[searchChild], this.queue[index]];

            index = searchChild;
            left = 2 * index + 1;
            searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;
        }

        return out;
    }

    size() {
        return this.queue.length;
    }
    compare(index1, index2) {
        if (this.queue[index1] === undefined) return 1;
        if (this.queue[index2] === undefined) return -1;

        return this.compareFn(this.queue[index1], this.queue[index2]);
    }

}

const topKFrequent = function (nums, k) {
    const map = new Map();

    for (const num of nums) {
        map.set(num, (map.get(num) || 0) + 1);
    }

    const heap= new Heap((a, b) => a[1] - b[1]);

    for (const entry of map.entries()) {
        heap.push(entry);

        if (heap.size() > k) {
            heap.pop();
        }
    }

    const res = [];

    for (let i = heap.size() - 1; i >= 0; i--) {
        res[i] = heap.pop()[0];
    }

    return res;
};

TypeScript:

function topKFrequent(nums: number[], k: number): number[] {
    const countMap: Map<number, number> = new Map();
    for (let num of nums) {
        countMap.set(num, (countMap.get(num) || 0) + 1);
    }
    // TypeScript lacks a min-heap structure, so sorting the entire array and taking the top k is utilized.
    return [...countMap.entries()]
        .sort((a, b) => b[1] - a[1])
        .slice(0, k)
        .map(i => i[0]);
};

C#:

public int[] TopKFrequent(int[] nums, int k) {
    //Map-Key mapping weights
    Dictionary<int,int> dic = new();
    for(int i = 0; i < nums.Length; i++){
        if(dic.ContainsKey(nums[i])){
            dic[nums[i]]++;
        }else{
            dic.Add(nums[i], 1);
        }
    }
    //PriorityQueue—Sorted ascending
    PriorityQueue<int,int> pq = new();
    foreach(var num in dic){
        pq.Enqueue(num.Key, num.Value);
        if(pq.Count > k){
            pq.Dequeue();
        }
    }
    
    // //Stack-verturned the results
    // Stack<int> res = new();
    // while(pq.Count > 0){
    //     res.Push(pq.Dequeue());
    // }
    // return res.ToArray();

    //Array conversion
    int[] res = new int[k];
    for(int i = k - 1; i >= 0; i--){
        res[i] = pq.Dequeue();
    }
    return res;
}

Scala:

Solution 1: Priority Queue

object Solution {
  import scala.collection.mutable
  def topKFrequent(nums: Array[Int], k: Int): Array[Int] = {
    val map = mutable.HashMap[Int, Int]()
    for (num <- nums) {
      map.put(num, map.getOrElse(num, 0) + 1)
    }
    var queue = mutable.PriorityQueue[(Int, Int)]()(Ordering.fromLessThan((x, y) => x._2 > y._2))
    for (elem <- map) {
      queue.enqueue(elem)
      if(queue.size > k){ 
        queue.dequeue 
      }
    }
    queue.map(_._1).toArray
  }
}

Solution 2: Similar to a wordCount program

object Solution {
  def topKFrequent(nums: Array[Int], k: Int): Array[Int] = {
    nums.map((_, 1)).groupBy(_._1)
      .map {
        case (x, arr) => (x, arr.map(_._2).sum)
      }
      .toArray
      .sortWith(_._2 > _._2)
      .take(k)
      .map(_._1)
  }
}

Rust

Min-heap

use std::cmp::Reverse;
use std::collections::{BinaryHeap, HashMap};
impl Solution {
    pub fn top_k_frequent(nums: Vec<i32>, k: i32) -> Vec<i32> {
        let mut hash = HashMap::new();
        let mut heap = BinaryHeap::with_capacity(k as usize);
        nums.into_iter().for_each(|k| {
            *hash.entry(k).or_insert(0) += 1;
        });

        for (k, v) in hash {
            if heap.len() == heap.capacity() {
                if *heap.peek().unwrap() < (Reverse(v), k) {
                    continue;
                } else {
                    heap.pop();
                }
            }
            heap.push((Reverse(v), k));
        }
        heap.into_iter().map(|(_, k)| k).collect()
    }
}