keetcoder

Data structures and algorithms are often hidden in places we cannot see.

# 20. Valid Parentheses

LeetCode Problem Link (opens new window)

Given a string containing just the characters '(', ')', '{', '}', '[', ']', determine if the input string is valid.

A valid string must meet the following criteria:

  • Open brackets must be closed by the same type of brackets.
  • Open brackets must be closed in the correct order.
  • Note that an empty string is also considered valid.

Example 1:

  • Input: ()
  • Output: true

Example 2:

  • Input: ()[]{}
  • Output: true

Example 3:

  • Input: (]
  • Output: false

Example 4:

  • Input: ([)]
  • Output: false

Example 5:

  • Input: {[]}
  • Output: true

# Approach

# Additional Notes

Bracket matching is a classic problem solved using a stack.

The problem is similar to how we write code and ensure that brackets are ordered correctly, with each opening bracket having a corresponding closing bracket.

If you remember compiler principles, the process of handling brackets such as parentheses during lexical analysis is also done using stack data structures.

Another example is the Linux system command cd, which we're all familiar with.

cd a/b/c/../../
1

This command results in entering directory a, but how does the system know to end up in a? This is where the stack's application comes into play (this could also be a relevant interview question).

Thus, stacks are widely used in computer science.

Some students often wonder what use these data structures have, thinking they don't help in developing software. Most students refer to visual software such as apps or websites, which are very high-level applications. Many underlying functionalities are implemented using fundamental data structures and algorithms.

So, the application of data structures and algorithms is often hidden where we can't see them!

Let's get to the problem.

# Starting the Solution

Given the special properties of stack structures, they are particularly suitable for symmetry matching problems.

First, we need to clarify the mismatch situations of brackets in the string.

Some students start coding immediately in interviews upon seeing this problem and then find themselves getting more and more confused.

In such situations, I recommend analyzing all mismatch scenarios before writing any code to avoid ending up with erroneous logic.

To analyze, there are three main mismatch situations:

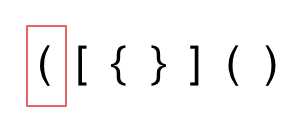
  1. First, there may be extra opening brackets in the string, resulting in an invalid sequence. Mismatched Brackets 1

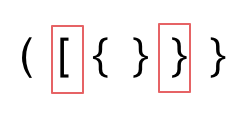
  2. Secondly, even if brackets aren't extra, the types may not match up. Mismatched Brackets 2

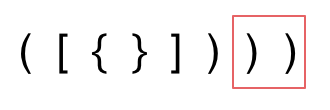
  3. Lastly, there may be extra closing brackets, leading to mismatches. Mismatched Brackets 3

Our code should handle these three mismatch conditions to avoid issues. It demonstrates the importance of analysis before jumping into implementation.

The animation below illustrates this:

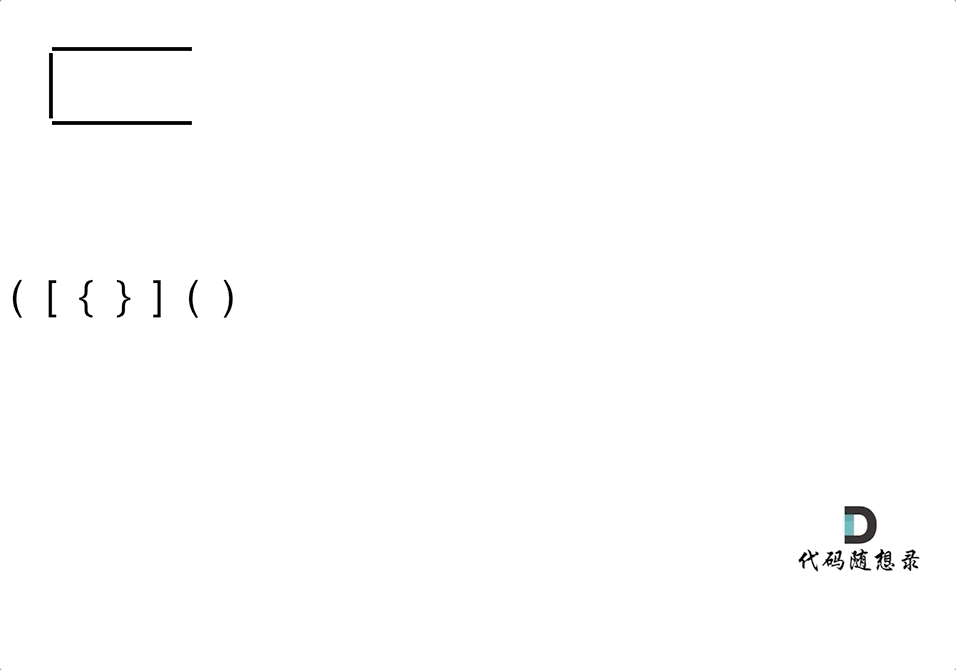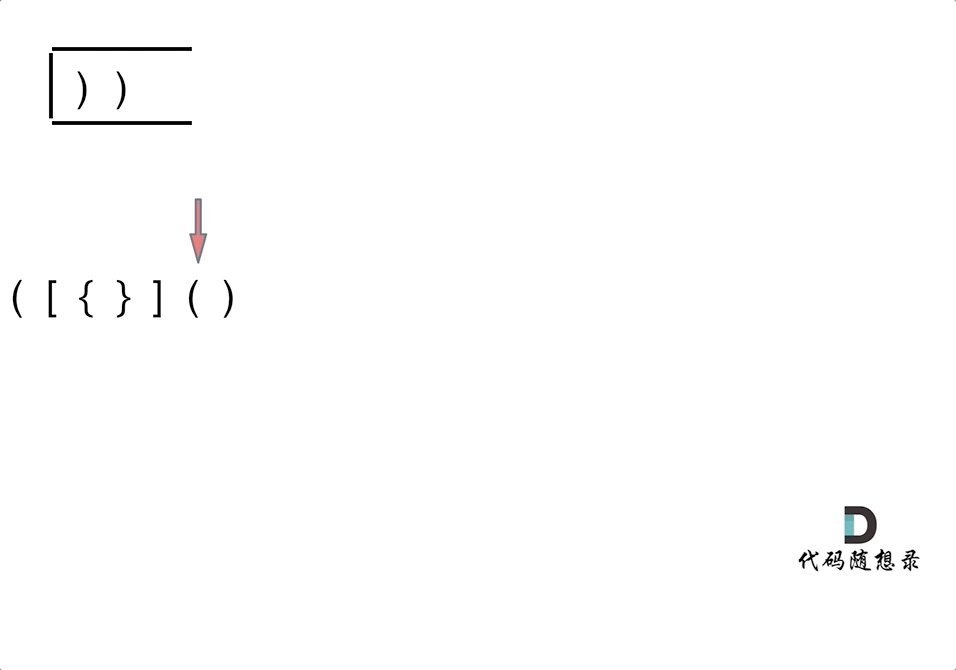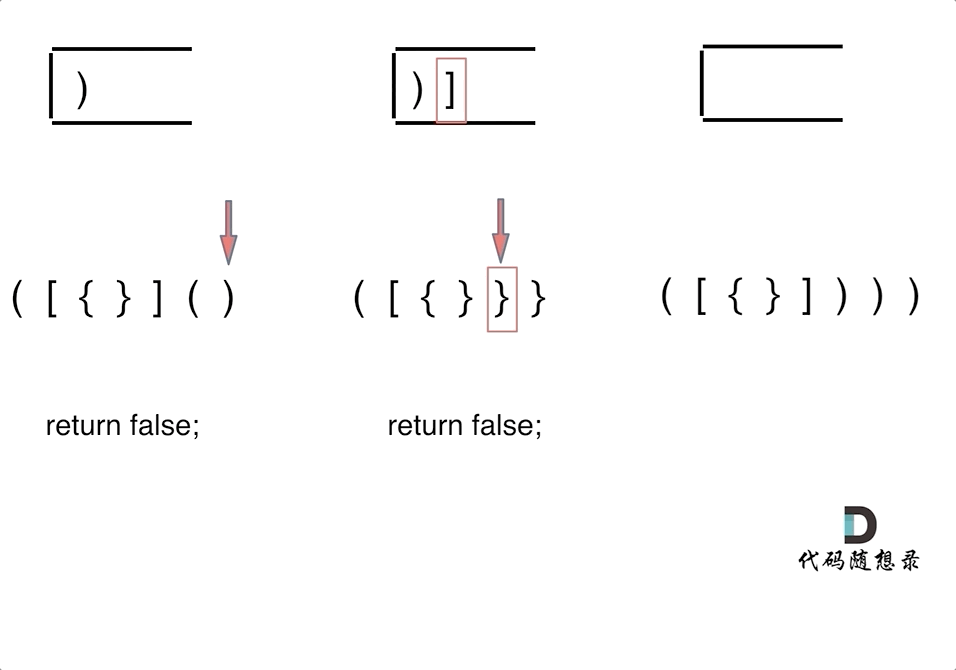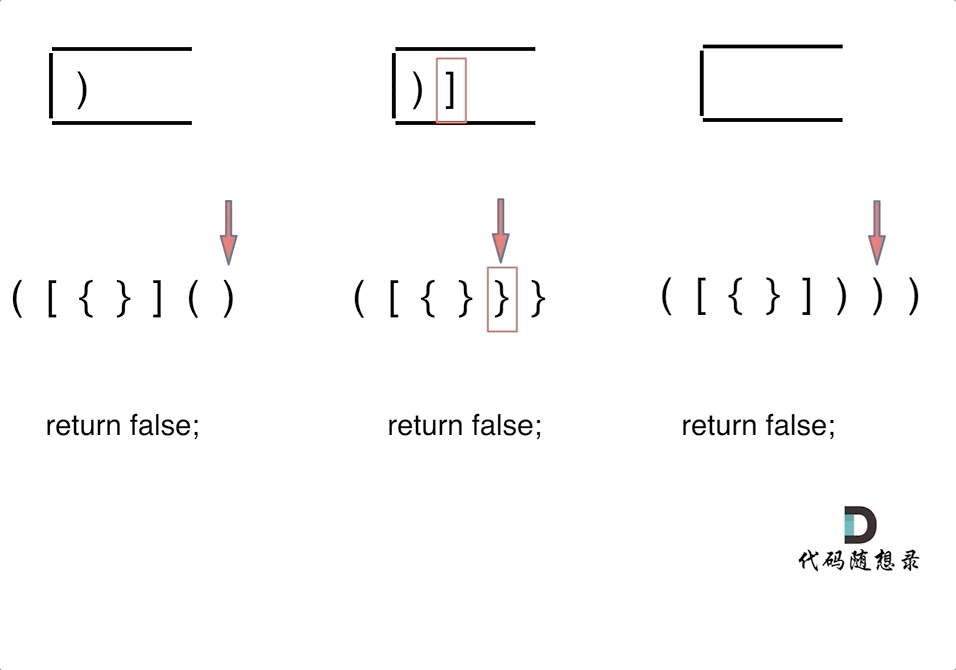
20. Valid Parentheses

Situation 1: If we have traversed the string and the stack isn't empty, it means some opening brackets lack matching closing brackets, so we return false.

Situation 2: During the string traversal, if the intended character cannot be matched from the stack, we return false.

Situation 3: While traversing, if the stack is already empty and lacks matching characters, it means closing brackets do not have corresponding opening brackets, so we return false.

When are open and close brackets fully matched? It's when the string traversal completes, and the stack is empty, indicating all brackets are matched.

After this analysis, writing the code becomes straightforward.

Additionally, a useful trick is to push corresponding closing brackets on seeing open brackets, and we only need to compare the current element with the stack top. This approach simplifies implementation compared to pushing open brackets first.

Here's the C++ implementation:

class Solution {
public:
    bool isValid(string s) {
        if (s.size() % 2 != 0) return false; // If the length of s is odd, it can't be valid
        stack<char> st;
        for (int i = 0; i < s.size(); i++) {
            if (s[i] == '(') st.push(')');
            else if (s[i] == '{') st.push('}');
            else if (s[i] == '[') st.push(']');
            // Case 3: During traversal, the stack is already empty, and there are no matching characters left, so return false
            // Case 2: During traversal, the intended match isn't found in the stack, so return false
            else if (st.empty() || st.top() != s[i]) return false;
            else st.pop(); // Matching character found, pop the top of the stack
        }
        // Case 1: After traversal, if the stack isn't empty, it means there are unmatched open brackets, so return false; otherwise return true
        return st.empty();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
  • Time complexity: O(n)
  • Space complexity: O(n)

These tricks require exposure and practice to master and apply flexibly.

# Implementations in Other Languages

# Java:

class Solution {
    public boolean isValid(String s) {
        Deque<Character> deque = new LinkedList<>();
        char ch;
        for (int i = 0; i < s.length(); i++) {
            ch = s.charAt(i);
            // On encountering a left bracket, push the corresponding right bracket onto the stack
            if (ch == '(') {
                deque.push(')');
            }else if (ch == '{') {
                deque.push('}');
            }else if (ch == '[') {
                deque.push(']');
            } else if (deque.isEmpty() || deque.peek() != ch) {
                return false;
            }else {
                deque.pop();
            }
        }
        // If the stack is empty at the end of traversal, it implies complete bracket matching
        return deque.isEmpty();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// Alternative solution
// Directly check if the corresponding half is at the stack’s top
class Solution {
    public boolean isValid(String s) {
        Stack<Character> stack = new Stack<>();
        for(char c : s.toCharArray()){
            // If the corresponding character is found, proceed to match
            if(c == ')' && !stack.isEmpty() && stack.peek() == '(')
                stack.pop();
            else if(c == '}' && !stack.isEmpty() && stack.peek() == '{')
                stack.pop();
            else if(c == ']' && !stack.isEmpty() && stack.peek() == '[')
                stack.pop();
            else
                stack.push(c); // If unmatched, just push it
        }

        return stack.isEmpty();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# Python:

# Method 1: Use only stack for space efficiency
class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        
        for item in s:
            if item == '(':
                stack.append(')')
            elif item == '[':
                stack.append(']')
            elif item == '{':
                stack.append('}')
            elif not stack or stack[-1] != item:
                return False
            else:
                stack.pop()
        
        return True if not stack else False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Method 2: Use dictionary
class Solution:
    def isValid(self, s: str) -> bool:
        stack = []
        mapping = {
            '(': ')',
            '[': ']',
            '{': '}'
        }
        for item in s:
            if item in mapping.keys():
                stack.append(mapping[item])
            elif not stack or stack[-1] != item: 
                return False
            else: 
                stack.pop()
        return True if not stack else False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# Go:

// Approach: Use a stack for matching brackets
// Time complexity O(n)
// Space complexity O(n)
func isValid(s string) bool {
	// Use slice to simulate stack
	stack := make([]rune, 0)

	// m records left brackets matching specific right brackets
	m := make(map[rune]rune)
	m[')'] = '('
	m[']'] = '['
	m['}'] = '{'

	// Traverse through the string
	for _, c := range s {
		// Left brackets directly push into the stack
		if c == '(' || c == '[' || c == '{' {
			stack = append(stack, c)
		} else {
			// If the stack is empty or unmatched, return false
			if len(stack) == 0 || stack[len(stack)-1] != m[c] {
				return false
			}
			// Simulate stack pop
			stack = stack[:len(stack)-1]
		}
	}

	// Return true if the stack is empty (complete matching)
	return len(stack) == 0
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# Ruby:

def is_valid(strs)
    symbol_map = {')' => '(', '}' => '{', ']' => '['}
    stack = []
    strs.size.times {|i|
        c = strs[i]
        if symbol_map.has_key?(c)
            top_e = stack.shift
            return false if symbol_map[c] != top_e
        else
            stack.unshift(c)
        end
    }
    stack.empty?
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# JavaScript:

var isValid = function (s) {
  const stack = [];
  for (let i = 0; i < s.length; i++) {
    let c = s[i];
    switch (c) {
      case '(':
        stack.push(')');
        break;
      case '[':
        stack.push(']');
        break;
      case '{':
        stack.push('}');
        break;
      default:
        if (c !== stack.pop()) {
          return false;
        }
    }
  }
  return stack.length === 0;
};
// Simplified version
var isValid = function(s) {
    const stack = [], 
        map = {
            "(":")",
            "{":"}",
            "[":"]"
        };
    for(const x of s) {
        if(x in map) {
            stack.push(x);
            continue;
        };
        if(map[stack.pop()] !== x) return false;
    }
    return !stack.length;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# TypeScript:

Version 1: Basic

function isValid(s: string): boolean {
    let helperStack: string[] = [];
    for (let i = 0, length = s.length; i < length; i++) {
        let x: string = s[i];
        switch (x) {
            case '(':
                helperStack.push(')');
                break;
            case '[':
                helperStack.push(']');
                break;
            case '{':
                helperStack.push('}');
                break;
            default:
                if (helperStack.pop() !== x) return false;
                break;
        }
    }
    return helperStack.length === 0;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Version 2: Optimized

function isValid(s: string): boolean {
    type BracketMap = {
        [index: string]: string;
    }
    let helperStack: string[] = [];
    let bracketMap: BracketMap = {
        '(': ')',
        '[': ']',
        '{': '}'
    }
    for (let i of s) {
        if (bracketMap.hasOwnProperty(i)) {
            helperStack.push(bracketMap[i]);
        } else if (i !== helperStack.pop()) {
            return false;
        }
    }
    return helperStack.length === 0;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# Swift:

func isValid(_ s: String) -> Bool {
    var stack = [String.Element]()
    for ch in s {
        if ch == "(" {
            stack.append(")")
        } else if ch == "{" {
            stack.append("}")
        } else if ch == "[" {
            stack.append("]")
        } else {
            let top = stack.last
            if ch == top {
                stack.removeLast()
            } else {
                return false
            }
        }
    }
    return stack.isEmpty
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# C:

// Helper function: Checks if the top element of the stack and the input bracket form a pair. If not, return false
int notMatch(char par, char* stack, int stackTop) {
    switch(par) {
        case ']':
            return stack[stackTop - 1] != '[';
        case ')':
            return stack[stackTop - 1] != '(';
        case '}':
            return stack[stackTop - 1] != '{';
    }
    return 0;
}

bool isValid(char * s){
    int strLen = strlen(s);
    // Allocate space for the stack
    char stack[5000];
    int stackTop = 0;

    // Traverse the string
    int i;
    for(i = 0; i < strLen; i++) {
        // Get the current character
        char tempChar = s[i];
        // If it's an opening bracket, push it to the stack
        if(tempChar == '(' || tempChar == '[' || tempChar == '{')
            stack[stackTop++] = tempChar;
        // If it's a closing bracket and no matching opening bracket in the stack, return false
        else if(stackTop == 0 || notMatch(tempChar, stack, stackTop))
            return 0;
        // Valid pair found, pop the stack
        else
            stackTop--;
    }
    // Return true if stack is empty, false otherwise
    return !stackTop;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# C#:

public class Solution {
    public bool IsValid(string s) {
        var len = s.Length;
        if(len % 2 == 1) return false; // If string length is odd, return false
        // Initialize stack
        var stack = new Stack<char>();
        // Traverse the string
        for(int i = 0; i < len; i++){
            // On encountering a left bracket, push corresponding right bracket to the stack
            if(s[i] == '('){
                stack.Push(')');
            }else if(s[i] == '['){
                stack.Push(']');
            }else if(s[i] == '{'){
                stack.Push('}');
            }
            // If there are no matching characters left, return false
            else if(stack.Count == 0 || stack.Pop() != s[i])
                return false;
        }
        // Return true if stack is empty, false otherwise
        return stack.Count == 0;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# PHP:

// https://www.php.net/manual/zh/class.splstack.php
class Solution
{
    function isValid($s){
        $stack = new SplStack();
        for ($i = 0; $i < strlen($s); $i++) {
            if ($s[$i] == "(") {
                $stack->push(')');
            } else if ($s[$i] == "{") {
                $stack->push('}');
            } else if ($s[$i] == "[") {
                $stack->push(']');
            // 2. During traversal, if no matching character is found, return false
            // 3. If the stack is already empty and unmatched, return false
            } else if ($stack->isEmpty() || $stack->top() != $s[$i]) {
                return false;
            } else {// Matching character found, pop
                $stack->pop();
            }
        }
        // 1. If traversal ends with unmatched open brackets, return false
        return $stack->isEmpty();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# Scala:

object Solution {
  import scala.collection.mutable
  def isValid(s: String): Boolean = {
    if(s.length % 2 != 0) return false    // If string length is odd, return false
    val stack = mutable.Stack[Char]()
    // Traverse the string
    for (i <- s.indices) {
      val c = s(i)
      if (c == '(' || c == '[' || c == '{') stack.push(c)
      else if(stack.isEmpty) return false   // If no opening bracket, return false immediately
      // Return false for the following unmet conditions        
      else if(c==')' && stack.pop() != '(') return false 
      else if(c==']' && stack.pop() != '[') return false 
      else if(c=='}' && stack.pop() != '{') return false 
    }
    // Return true if stack is empty (all matched)
    stack.isEmpty
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# Rust:

impl Solution {
    pub fn is_valid(s: String) -> bool {
        if s.len() % 2 == 1 {
            return false;
        }
        let mut stack = vec![];
        let mut chars: Vec<char> = s.chars().collect();
        while let Some(s) = chars.pop() {
            match s {
                ')' => stack.push('('),
                ']' => stack.push('['),
                '}' => stack.push('{'),
                _ => {
                    if stack.is_empty() || stack.pop().unwrap() != s {
                        return false;
                    }
                }
            }
        }
        stack.is_empty()
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Last updated:: 9/4/2025, 3:19:38 PM

← 5. Remove All Adjacent Duplicates in String →

Copyright © 2025 keetcoder