232. Implement Queue using Stacks

LeetCode Problem Link (opens new window)

Implement the following operations of a queue using stacks:

• push(x) -- Push element x to the back of queue.
• pop() -- Removes the element from in front of queue.
• peek() -- Get the front element.
• empty() -- Return whether the queue is empty.

Example:

MyQueue queue = MyQueue();
queue.push(1);
queue.push(2);
queue.peek();  // returns 1
queue.pop();   // returns 1
queue.empty(); // returns false

Notes:

• You must use only standard operations of a stack -- which means only push to top, peek/pop from top, size, and is empty operations are valid.
• Depending on your language, stack may not be supported natively. You may simulate a stack by using a list or deque (double-ended queue) as long as you use only standard operations of a stack.
• You can assume all operations are valid (e.g., no pop or peek operations will be called on an empty queue).

Approach

This is a simulation problem that does not involve specific algorithms but assesses the understanding of stacks and queues.

Using stacks to simulate queue behavior requires more than one stack; thus, two stacks are needed: an input stack and an output stack. It's crucial to understand the relationship between these stacks.

The following animation illustrates the execution steps of the queue:

Execute statements:

• queue.push(1);
• queue.push(2);
• queue.pop(); Notice the operation on the output stack
• queue.push(3);
• queue.push(4);
• queue.pop();
• queue.pop(); Notice the operation on the output stack
• queue.pop();
• queue.empty();

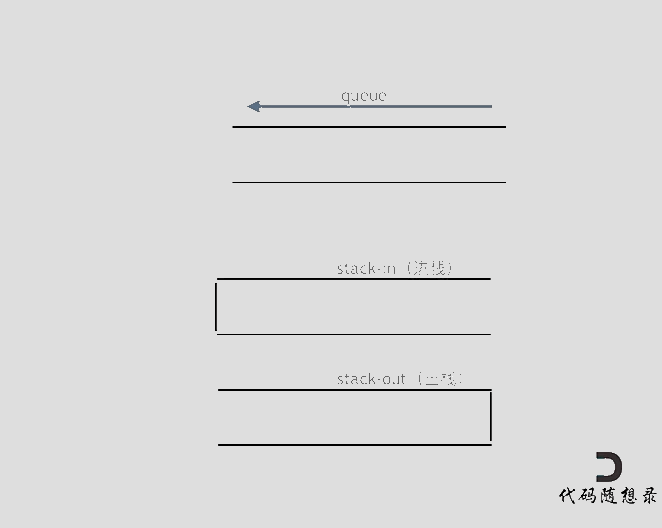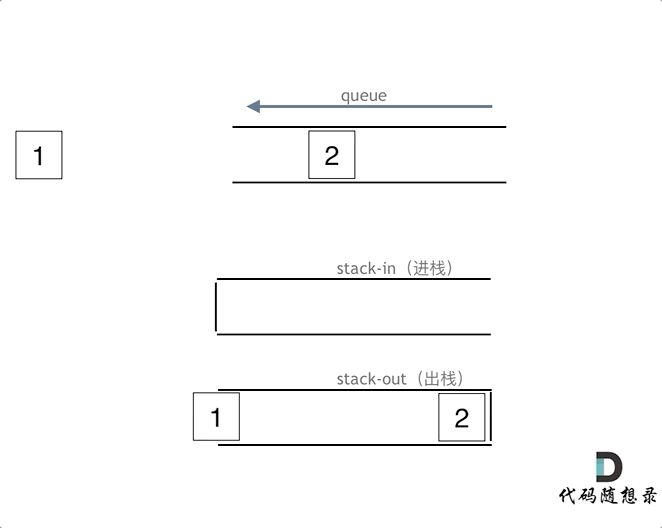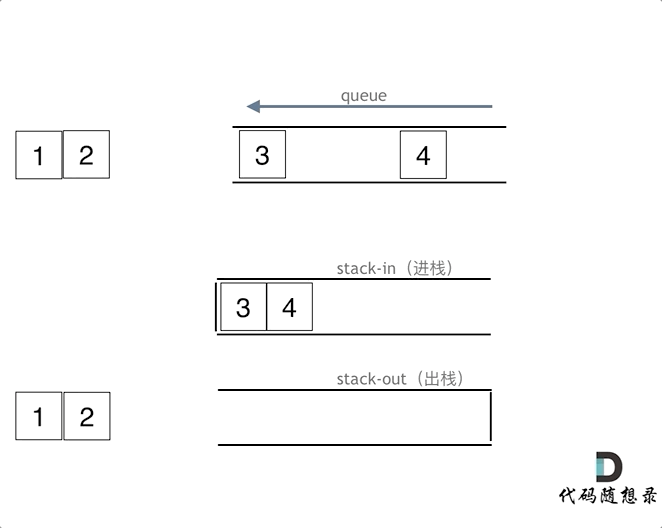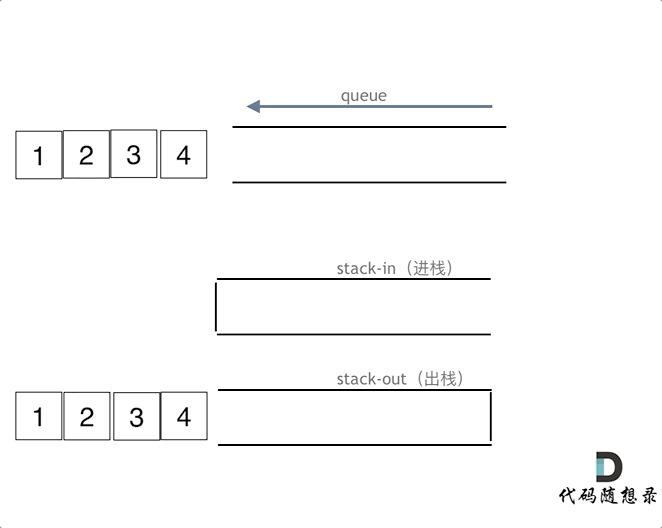
When pushing data, it is sufficient to push data into the input stack. When popping, if the output stack is empty, all data from the input stack is transferred (note it must all be transferred) to the output stack, then popped from there. If the output stack is not empty, simply pop from it.

Finally, to determine if the queue is empty, check if both the input and output stacks are empty.

In the code implementation, you'll notice that the pop() and peek() functions are similar, which can be abstracted for cleaner code.

C++ Implementation:

class MyQueue {
public:
    stack<int> stIn;
    stack<int> stOut;
    /** Initialize your data structure here. */
    MyQueue() {

    }
    /** Push element x to the back of queue. */
    void push(int x) {
        stIn.push(x);
    }

    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        // Only transfer data from stIn to stOut if stOut is empty
        if (stOut.empty()) {
            while(!stIn.empty()) {
                stOut.push(stIn.top());
                stIn.pop();
            }
        }
        int result = stOut.top();
        stOut.pop();
        return result;
    }

    /** Get the front element. */
    int peek() {
        int res = this->pop(); // Use existing pop function
        stOut.push(res); // Push it back since pop removes the element
        return res;
    }

    /** Returns whether the queue is empty. */
    bool empty() {
        return stIn.empty() && stOut.empty();
    }
};

• Time Complexity: All operations are (O(1)). Although pop and peek operations appear to be (O(n)), each element is moved exactly twice, so the overall complexity is (O(1)).
• Space Complexity: (O(n)).

Extension

Observe that peek() directly reuses pop() to avoid rewriting the empty check logic of stOut.

In industrial-level code development, one should avoid simply copying and pasting similar functions with slight modifications. This leads to messy code, making the project unsustainable. Always aim for code reuse and abstraction.

Other Language Versions

Java:

class MyQueue {

    Stack<Integer> stackIn;
    Stack<Integer> stackOut;

    /** Initialize your data structure here. */
    public MyQueue() {
        stackIn = new Stack<>(); // Input stack
        stackOut = new Stack<>(); // Output stack
    }
    
    /** Push element x to the back of queue. */
    public void push(int x) {
        stackIn.push(x);
    }
    
    /** Removes the element from in front of queue and returns that element. */
    public int pop() {    
        dumpstackIn();
        return stackOut.pop();
    }
    
    /** Get the front element. */
    public int peek() {
        dumpstackIn();
        return stackOut.peek();
    }
    
    /** Returns whether the queue is empty. */
    public boolean empty() {
        return stackIn.isEmpty() && stackOut.isEmpty();
    }

    // Transfer elements if out stack is empty
    private void dumpstackIn(){
        if (!stackOut.isEmpty()) return; 
        while (!stackIn.isEmpty()){
                stackOut.push(stackIn.pop());
        }
    }
}

Python:

class MyQueue:

    def __init__(self):
        """
        in is for push; out is for pop
        """
        self.stack_in = []
        self.stack_out = []

    def push(self, x: int) -> None:
        """
        Push new element into stack_in
        """
        self.stack_in.append(x)

    def pop(self) -> int:
        """
        Removes the element from in front of queue and returns it
        """
        if self.empty():
            return None
        
        if self.stack_out:
            return self.stack_out.pop()
        else:
            for i in range(len(self.stack_in)):
                self.stack_out.append(self.stack_in.pop())
            return self.stack_out.pop()

    def peek(self) -> int:
        """
        Get the front element
        """
        ans = self.pop()
        self.stack_out.append(ans)
        return ans

    def empty(self) -> bool:
        """
        Return if both stacks are empty
        """
        return not (self.stack_in or self.stack_out)

Go:

// Using slices to implement a stack

type MyStack []int

func (s *MyStack) Push(v int) {
    *s = append(*s, v)
}

func (s *MyStack) Pop() int {
    val := (*s)[len(*s)-1]
    *s = (*s)[:len(*s)-1]
    return val
}

func (s *MyStack) Peek() int {
    return (*s)[len(*s)-1]
}

func (s *MyStack) Size() int {
    return len(*s)
}

func (s *MyStack) Empty() bool {
    return s.Size() == 0
}

// Implementation for MyQueue

type MyQueue struct {
    stackIn  *MyStack
    stackOut *MyStack
}

func Constructor() MyQueue {
    return MyQueue{
        stackIn:  &MyStack{},
        stackOut: &MyStack{},
    }
}

func (this *MyQueue) Push(x int) {
    this.stackIn.Push(x)
}

func (this *MyQueue) Pop() int {
    this.fillStackOut()
    return this.stackOut.Pop()
}

func (this *MyQueue) Peek() int {
    this.fillStackOut()
    return this.stackOut.Peek()
}

func (this *MyQueue) Empty() bool {
    return this.stackIn.Empty() && this.stackOut.Empty()
}

// Fill the output stack
func (this *MyQueue) fillStackOut() {
    if this.stackOut.Empty() {
        for !this.stackIn.Empty() {
            val := this.stackIn.Pop()
            this.stackOut.Push(val)
        }
    }
}

JavaScript:

// Implementing queue using two arrays as stacks

var MyQueue = function() {
    this.stackIn = [];
    this.stackOut = [];
};

MyQueue.prototype.push = function(x) {
    this.stackIn.push(x);
};

MyQueue.prototype.pop = function() {
    const size = this.stackOut.length;
    if(size) {
        return this.stackOut.pop();
    }
    while(this.stackIn.length) {
        this.stackOut.push(this.stackIn.pop());
    }
    return this.stackOut.pop();
};

MyQueue.prototype.peek = function() {
    const x = this.pop();
    this.stackOut.push(x);
    return x;
};

MyQueue.prototype.empty = function() {
    return !this.stackIn.length && !this.stackOut.length
};

TypeScript:

class MyQueue {
    private stackIn: number[]
    private stackOut: number[]
    constructor() {
        this.stackIn = [];
        this.stackOut = [];
    }

    push(x: number): void {
        this.stackIn.push(x);
    }

    pop(): number {
        if (this.stackOut.length === 0) {
            while (this.stackIn.length > 0) {
                this.stackOut.push(this.stackIn.pop()!);
            }
        }
        return this.stackOut.pop()!;
    }

    peek(): number {
        let temp: number = this.pop();
        this.stackOut.push(temp);
        return temp;
    }

    empty(): boolean {
        return this.stackIn.length === 0 && this.stackOut.length === 0;
    }
}

Swift:

class MyQueue {
    
    var stackIn = [Int]()
    var stackOut = [Int]()
    
    init() {}
    
    func push(_ x: Int) {
        stackIn.append(x)
    }
    
    func pop() -> Int {
        if stackOut.isEmpty {
            while !stackIn.isEmpty {
                stackOut.append(stackIn.popLast()!)
            }
        }
        return stackOut.popLast() ?? -1
    }
    
    func peek() -> Int {
        let res = pop()
        stackOut.append(res)
        return res
    }
    
    func empty() -> Bool {
        return stackIn.isEmpty && stackOut.isEmpty
    }
}

C:

typedef struct {
    int stackInTop, stackOutTop;
    int stackIn[100], stackOut[100];
} MyQueue;

MyQueue* myQueueCreate() {
    MyQueue* queue = (MyQueue*)malloc(sizeof(MyQueue));
    queue->stackInTop = 0;
    queue->stackOutTop = 0;
    return queue;
}

void myQueuePush(MyQueue* obj, int x) {
    obj->stackIn[(obj->stackInTop)++] = x;
}

int myQueuePop(MyQueue* obj) {
    int stackInTop = obj->stackInTop;
    int stackOutTop = obj->stackOutTop;
    if(stackOutTop == 0) {
        while(stackInTop > 0) {
            obj->stackOut[stackOutTop++] = obj->stackIn[--stackInTop];
        }
    }
    int top = obj->stackOut[--stackOutTop];
    while(stackOutTop > 0) {
        obj->stackIn[stackInTop++] = obj->stackOut[--stackOutTop];
    }
    obj->stackInTop = stackInTop;
    obj->stackOutTop = stackOutTop;
    return top;
}

int myQueuePeek(MyQueue* obj) {
    return obj->stackIn[0];
}

bool myQueueEmpty(MyQueue* obj) {
    return obj->stackInTop == 0 && obj->stackOutTop == 0;
}

void myQueueFree(MyQueue* obj) {
    obj->stackInTop = 0;
    obj->stackOutTop = 0;
}

C#:

public class MyQueue {
    Stack<int> inStack;
    Stack<int> outStack;

    public MyQueue() {
        inStack = new Stack<int>();
        outStack = new Stack<int>();
    }
    
    public void Push(int x) {
        inStack.Push(x);
    }
    
    public int Pop() {
        dumpstackIn();
        return outStack.Pop();
    }
    
    public int Peek() {
        dumpstackIn();
        return outStack.Peek();
    }
    
    public bool Empty() {
        return inStack.Count == 0 && outStack.Count == 0;
    }

    private void dumpstackIn(){
        if (outStack.Count != 0) return; 
        while(inStack.Count != 0){
            outStack.Push(inStack.Pop());
        }
    }
}

PHP:

class MyQueue {
    private $stackIn;
    private $stackOut;
    
    function __construct() {
        $this->stackIn = new SplStack();
        $this->stackOut = new SplStack();
    }

    function push($x) {
        $this->stackIn->push($x);
    }

    function pop() {
        $this->peek();
        return $this->stackOut->pop();
    }

    function peek() {
        if($this->stackOut->isEmpty()){
            $this->shift();
        }
        return $this->stackOut->top();
    }

    function empty() {
        return $this->stackOut->isEmpty() && $this->stackIn->isEmpty();
    }

    private function shift(){
        while(!$this->stackIn->isEmpty()){
            $this->stackOut->push($this->stackIn->pop());
        }
    }
}

Scala:

class MyQueue() {
  import scala.collection.mutable
  val stackIn = mutable.Stack[Int]()
  val stackOut = mutable.Stack[Int]()

  def push(x: Int) {
    stackIn.push(x)
  }

  def dumpStackIn(): Unit = {
    if (!stackOut.isEmpty) return
    while (!stackIn.isEmpty) {
      stackOut.push(stackIn.pop())
    }
  }

  def pop(): Int = {
    dumpStackIn()
    stackOut.pop()
  }

  def peek(): Int = {
    dumpStackIn()
    val res: Int = stackOut.pop()
    stackOut.push(res)
    res
  }

  def empty(): Boolean = {
    stackIn.isEmpty && stackOut.isEmpty
  }

}

Rust:

struct MyQueue {
    stack_in: Vec<i32>,
    stack_out: Vec<i32>,
}
impl MyQueue {
    fn new() -> Self {
        MyQueue {
            stack_in: Vec::new(),
            stack_out: Vec::new(),
        }
        
    }
    
    fn push(&mut self, x: i32) {
        self.stack_in.push(x);
    }
    
    fn pop(&mut self) -> i32 {
        if self.stack_out.is_empty(){
            while !self.stack_in.is_empty() {
                self.stack_out.push(self.stack_in.pop().unwrap());
            }
        }
        self.stack_out.pop().unwrap()
    }
    
    fn peek(&mut self) -> i32 {
        let res = self.pop();
        self.stack_out.push(res);
        res
    }
    
    fn empty(&self) -> bool {
       self.stack_in.is_empty() && self.stack_out.is_empty()
    }
}