It still feels a bit awkward to implement a stack using a queue.

225. Implement Stack using Queues

LeetCode problem link (opens new window)

Implement a last in first out (LIFO) stack using only basic operations of a queue:

• push(x) -- Push element x onto the stack
• pop() -- Removes the element on top of the stack
• top() -- Get the top element
• empty() -- Return whether the stack is empty

Note:

• You can only use basic operations of a queue -- i.e., push to back, peek/pop from front, size, and is empty operations are valid.
• The language you are using might not support queues. You can use a list or deque (double-ended queue) to simulate a queue as long as it is standard queue operations.
• You may assume that all operations are valid (for example, no pop or top operations will be called on an empty stack).

Thought Process

(Here, it should be emphasized that it is a single-ended queue)

Some students might wonder about the practical engineering significance of such problems. In fact, many algorithm problems are mainly about testing and teaching the knowledge points, and this significance outweighs their engineering practical significance. Interview questions are often like this as well!

If you have recently tackled the stack and queue: How about I use a stack to implement a queue? (opens new window), you might still think of using an input queue and an output queue to simulate stack functionality. Think carefully, and it really doesn't work!

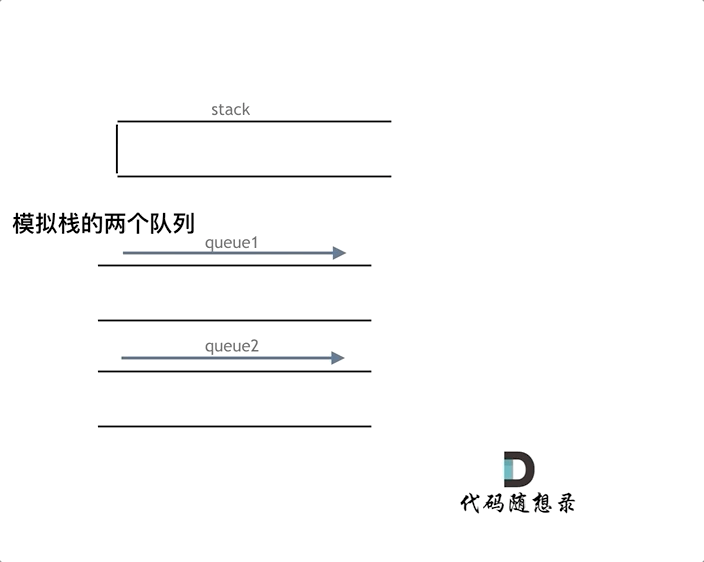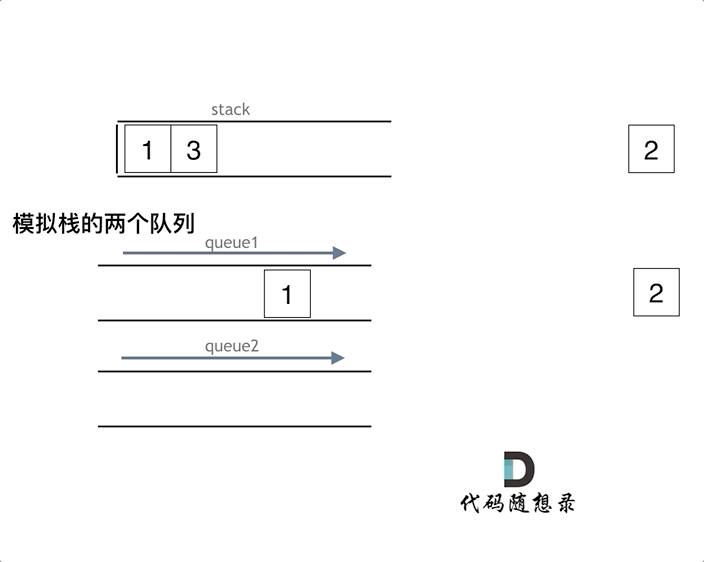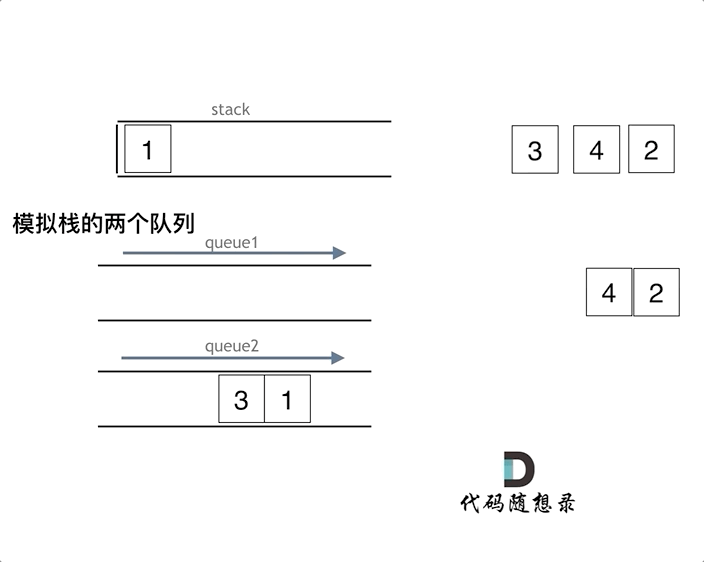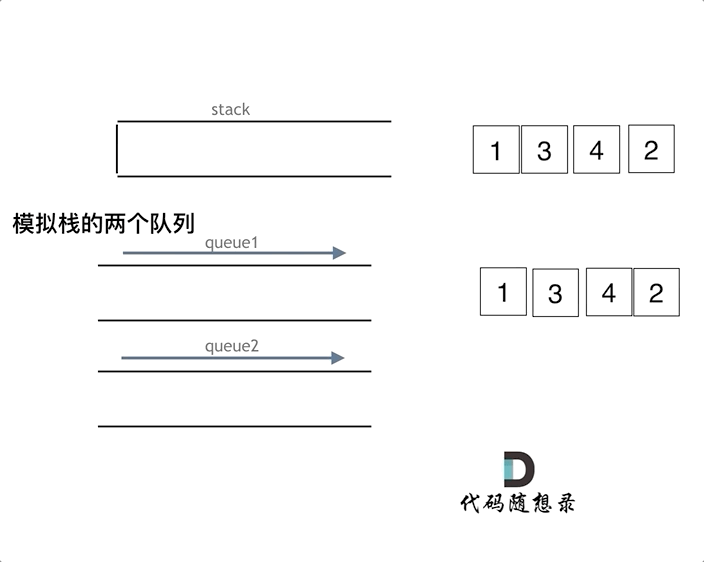
A stack implemented using a queue, actually, one queue is enough. Let’s first talk about the two-queue approach for implementing stack functionality.

A queue follows the first-in-first-out rule, and transferring data from one queue to another does not change the data order to a first-in-last-out order.

So, using stacks to implement queues and using queues to implement stacks are quite different, as this depends on the nature of these two data structures.

However, we still need to use two queues to simulate a stack, but the other queue is purely for backup purposes!

As illustrated in the animation below, implement the stack function using two queues que1 and que2. Queue que2 serves merely as a backup; transfer all elements from que1 except the last one to que2, then pop the last element, and transfer the other elements back to que1 from que2.

The simulated queue execution statement is as follows:

queue.push(1);        
queue.push(2);        
queue.pop();   // Note the pop operation       
queue.push(3);        
queue.push(4);       
queue.pop();   // Note the pop operation    
queue.pop();    
queue.pop();    
queue.empty();    

Details are as shown in the code comments:

class MyStack {
public:
    queue<int> que1;
    queue<int> que2; // Backup queue

    /** Initialize your data structure here. */
    MyStack() {

    }

    /** Push element x onto stack. */
    void push(int x) {
        que1.push(x);
    }

    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int size = que1.size();
        size--;
        while (size--) { // Transfer que1 to que2, but leave the last element
            que2.push(que1.front());
            que1.pop();
        }

        int result = que1.front(); // The last remaining element is the result to return
        que1.pop();
        que1 = que2; // Assign que2 back to que1
        while (!que2.empty()) { // Empty que2
            que2.pop();
        }
        return result;
    }

    /** Get the top element.
     ** Cannot use back() directly.
     */
    int top(){
        int size = que1.size();
        size--;
        while (size--){
            // Transfer que1 to que2, but leave the last element
            que2.push(que1.front());
            que1.pop();
        }

        int result = que1.front(); // The last remaining element is the top value to return
        que2.push(que1.front()); // After getting the value, add the last element into que2 as well to maintain the original structure
        que1.pop();

        que1 = que2; // Assign que2 back to que1
        while (!que2.empty()){
            // Empty que2
            que2.pop();
        }
        return result;
    }

    /** Returns whether the stack is empty. */
    bool empty() {
        return que1.empty();
    }
};

• Time Complexity: Pop is O(N), top is O(N), others are O(1)
• Space Complexity: O(N)

Optimization

In fact, for this problem, one queue is enough.

When using one queue to mimic the functionality of pop in a stack, simply append all elements from the front to the back of the queue, excluding the last element. This results in a last-in, first-out order for popping.

Optimized C++ Code

class MyStack {
public:
    queue<int> que;

    MyStack() {

    }

    void push(int x) {
        que.push(x);
    }

    int pop() {
        int size = que.size();
        size--;
        while (size--) { // Re-append elements from the front to the back of the queue
            que.push(que.front());
            que.pop();
        }
        int result = que.front(); // Elements now pop in stack order
        que.pop();
        return result;
    }

    int top(){
        int size = que.size();
        size--;
        while (size--){
            // Re-append elements from the front to the back of the queue
            que.push(que.front());
            que.pop();
        }
        int result = que.front(); // The element obtained is the top element
        que.push(que.front()); // Maintain original structure by appending the popped element
        que.pop();
        return result;
    }

    bool empty() {
        return que.empty();
    }
};

• Time Complexity: Pop is O(N), top is O(N), others are O(1)
• Space Complexity: O(N)

Other Language Versions

Java:

Two Queue Solution - Method 1

class MyStack {

    Queue<Integer> queue1; // Queue same as stack
    Queue<Integer> queue2; // Auxiliary queue

    /** Initialize your data structure here. */
    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        queue2.offer(x); // Place in auxiliary queue
        while (!queue1.isEmpty()){
            queue2.offer(queue1.poll());
        }
        Queue<Integer> queueTemp;
        queueTemp = queue1;
        queue1 = queue2;
        queue2 = queueTemp; // Finally, exchange queue1 with queue2 to put all in queue1
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        return queue1.poll(); // Since queue1 maintains same element order as stack, pop, top, and empty just need to consider queue1
    }
    
    /** Get the top element. */
    public int top() {
        return queue1.peek();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return queue1.isEmpty();
    }
}

Two Queue Solution - Method 2

class MyStack {
    // q1 is the main queue, and its element order is the same as the stack
    Queue<Integer> q1 = new ArrayDeque<>();
    // q2 is only used temporarily
    Queue<Integer> q2 = new ArrayDeque<>();

    public MyStack() {

    }
    // When adding an element, move all elements in q1 to q2, then add the new element to q1, followed by all elements in q2 back to q1
    public void push(int x) {
        while (q1.size() > 0) {
            q2.add(q1.poll());
        }
        q1.add(x);
        while (q2.size() > 0) {
            q1.add(q2.poll());
        }
    }

    public int pop() {
        return q1.poll();
    }

    public int top() {
        return q1.peek();
    }

    public boolean empty() {
        return q1.isEmpty();
    }
}

Using Deque for Implementation

class MyStack {
    // Deque interface inherits the Queue interface
    // Queue add, poll, peek functions are equivalent to Deque's addLast, pollFirst, peekFirst
    Deque<Integer> que1; // Queue to keep the same elements as stack
    Deque<Integer> que2; // Auxiliary queue

    /** Initialize your data structure here. */
    public MyStack() {
        que1 = new ArrayDeque<>();
        que2 = new ArrayDeque<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        que1.addLast(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        int size = que1.size();
        size--;
        // Transfer que1 to que2 leaving the last element
        while (size-- > 0) {
            que2.addLast(que1.peekFirst());
            que1.pollFirst();
        }

        int res = que1.pollFirst();
        que1 = que2;
        que2 = new ArrayDeque<>();
        return res;
    }
    
    /** Get the top element. */
    public int top() {
        return que1.peekLast();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return que1.isEmpty();
    }
}

Single Deque Optimization

class MyStack {
    // Deque interface inherits the Queue interface
    // Queue add, poll, peek functions are equivalent to Deque's addLast, pollFirst, peekFirst
    Deque<Integer> que1;

    /** Initialize your data structure here. */
    public MyStack() {
        que1 = new ArrayDeque<>();
    }
    
    /** Push element x onto stack. */
    public void push(int x) {
        que1.addLast(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    public int pop() {
        int size = que1.size();
        size--;

        while (size-- > 0) {
            que1.addLast(que1.peekFirst());
            que1.pollFirst();
        }

        int res = que1.pollFirst();
        return res;
    }
    
    /** Get the top element. */
    public int top() {
        return que1.peekLast();
    }
    
    /** Returns whether the stack is empty. */
    public boolean empty() {
        return que1.isEmpty();
    }
}

Single Queue Optimization

class MyStack {

    Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<>();
    }

    // Every time a number is offered, reorder and place this number at the front of the queue
    public void push(int x) {
        queue.offer(x);
        int size = queue.size();
        // Relocate all but the last element
        while (size-- > 1)
            queue.offer(queue.poll());
    }

    public int pop() {
        return queue.poll();
    }

    public int top() {
        return queue.peek();
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

Java Optimization Using a Single Queue with Approach Similar to Carl's Tutorial

class MyStack {
    Queue<Integer> queue;
    
    public MyStack() {
        queue = new LinkedList<>();
    }
    
    public void push(int x) {
        queue.add(x);
    }
    
    public int pop() {
        rePosition();
        return queue.poll();
    }
    
    public int top() {
        rePosition();
        int result = queue.poll();
        queue.add(result);
        return result;
    }
    
    public boolean empty() {
        return queue.isEmpty();
    }

    public void rePosition(){
        int size = queue.size();
        size--;
        while(size-->0)
            queue.add(queue.poll());
    }
}

Python:

from collections import deque

class MyStack:

    def __init__(self):
        """
        In Python's standard Queue or SimpleQueue we can't perform peek operations
        or access using an index, which makes the top operation harder to implement.

        Using a list could work, but pop(0) would be O(n) in terms of time complexity.
        Thus, we use a deque that can be indexed to simulate and access like a peek.

        in - holds all the data
        out - used only during pop operations
        """
        self.queue_in = deque()
        self.queue_out = deque()

    def push(self, x: int) -> None:
        """
        Just append to the deque
        """
        self.queue_in.append(x)


    def pop(self) -> int:
        """
        1. Make sure the stack isn't empty
        2. Because of the FIFO nature of the queue, we only use queue_out during pop
        3. Transfer all elements from queue_in (except the last one) to queue_out
        4. Swap in and out, now out has just one element
        5. Pop from out, which is the last element of the original queue
        
        tip: This cannot be like a stack implementing a queue,
        because the other queue is also FIFO; to pop we can't just pop it like a stack.
        Hence, in only holds values and is swapped during pop.
        """
        if self.empty():
            return None

        for i in range(len(self.queue_in) - 1):
            self.queue_out.append(self.queue_in.popleft())
        
        self.queue_in, self.queue_out = self.queue_out, self.queue_in    # Swap queues
        return self.queue_out.popleft()

    def top(self) -> int:
        """
        Written Variation One:
        1. Primarily ensure not empty
        2. Only in the stored data, so return the first (really) the last in stack terms

        Written Variation Two:
        1. Primarily ensure not empty
        2. Because of queue's FIFO nature, we only use out during pop
        3. Transfer all elements from in (except last) to out
        4. Swap in, out queues, one remains
        5. Take last out element, also temp store
        6. Add that back to in's end
        """
        # Written Version One:
        # if self.empty():
        #     return None
        
        # return self.queue_in[-1]    # Actually using stack to fetch the end of queue_in

        # Written Version Two:
        if self.empty():
            return None

        for i in range(len(self.queue_in) - 1):
            self.queue_out.append(self.queue_in.popleft())
        
        self.queue_in, self.queue_out = self.queue_out, self.queue_in 
        temp = self.queue_out.popleft()   
        self.queue_in.append(temp)
        return temp


    def empty(self) -> bool:
        """
        Only in holds values, check if it's empty
        """
        return len(self.queue_in) == 0

Optimized with Single Queue Implementation

class MyStack:

    def __init__(self):
        self.que = deque()

    def push(self, x: int) -> None:
        self.que.append(x)

    def pop(self) -> int:
        if self.empty():
            return None
        for i in range(len(self.que)-1):
            self.que.append(self.que.popleft())
        return self.que.popleft()

    def top(self) -> int:
        # Written Method One:
        # if self.empty():
        #     return None
        # return self.que[-1]

        # Written Method Two:
        if self.empty():
            return None
        for i in range(len(self.que)-1):
            self.que.append(self.que.popleft())
        temp = self.que.popleft()
        self.que.append(temp)
        return temp

    def empty(self) -> bool:
        return not self.que

Go:

Two Queue Implementation

type MyStack struct {
    // Create two queues
    queue1 []int
    queue2 []int
}

func Constructor() MyStack {
    return MyStack{	// Initialize
        queue1: make([]int, 0),
        queue2: make([]int, 0),
    }
}

func (this *MyStack) Push(x int)  {
     // Initially put data in queue2
    this.queue2 = append(this.queue2, x)	
   // Move all elements from queue1 to queue2, swap the two queues
    this.Move()
}

func (this *MyStack) Move(){    
    if len(this.queue1) == 0{
        // Swap, queue1 becomes queue2, queue2 becomes empty
        this.queue1, this.queue2 = this.queue2, this.queue1
    } else {
        // Elements in queue1 starting from the head getting added to queue2
        this.queue2 = append(this.queue2, this.queue1[0])  
        this.queue1 = this.queue1[1:] // Remove the front element
        this.Move() // Repeat
    }
}

func (this *MyStack) Pop() int {
    val := this.queue1[0]
    this.queue1 = this.queue1[1:]	// Remove the front element
    return val
}

func (this *MyStack) Top() int {
    return this.queue1[0]	// Return directly
}

func (this *MyStack) Empty() bool {
return len(this.queue1) == 0
}

/**
 * Your MyStack object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Push(x);
 * param_2 := obj.Pop();
 * param_3 := obj.Top();
 * param_4 := obj.Empty();
 */

Single Queue Implementation

type MyStack struct {
    queue []int // Create one queue
}

/** Initialize your data structure here. */
func Constructor() MyStack {
    return MyStack{   // Initialize
        queue: make([]int, 0),
    }
}

/** Push element x onto stack. */
func (this *MyStack) Push(x int)  {
    // Add element
    this.queue = append(this.queue, x)
}

/** Removes the element on top of the stack and returns that element. */
func (this *MyStack) Pop() int {
    n := len(this.queue) - 1 // Determine length
    while n != 0 { // Add back every element except the last one
        val := this.queue[0]
        this.queue = this.queue[1:]
        this.queue = append(this.queue, val)
        n--
    }
    // Remove the top element
    val := this.queue[0]
    this.queue = this.queue[1:]
    return val
}

/** Get the top element. */
func (this *MyStack) Top() int {
    // Reuse Pop method, re-add the popped element
    val := this.Pop()
    this.queue = append(this.queue, val)
    return val
}

/** Returns whether the stack is empty. */
func (this *MyStack) Empty() bool {
    return len(this.queue) == 0
}

/**
 * Your MyStack object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Push(x);
 * param_2 := obj.Pop();
 * param_3 := obj.Top();
 * param_4 := obj.Empty();
 */

JavaScript:

Using Arrays (push, shift) to Simulate Queues

// Using two queues
/**
 * Initialize your data structure here.
 */
var MyStack = function() {
    this.queue1 = [];
    this.queue2 = [];
};

/**
 * Push element x onto stack. 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queue1.push(x);
};

/**
 * Removes the element on top of the stack and returns that element.
 * @return {number}
 */
MyStack.prototype.pop = function() {
    // Reduce times of swapping two queues; only swap when queue1 is empty
    if (!this.queue1.length) {
        [this.queue1, this.queue2] = [this.queue2, this.queue1];
    }
    while (this.queue1.length > 1) {
        this.queue2.push(this.queue1.shift());
    }
    return this.queue1.shift();
};

/**
 * Get the top element.
 * @return {number}
 */
MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue1.push(x);
    return x;
};

/**
 * Returns whether the stack is empty.
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return !this.queue1.length && !this.queue2.length;
};

// Using a single queue
/**
 * Initialize your data structure here.
 */
var MyStack = function() {
    this.queue = [];
};

/**
 * Push element x onto stack. 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queue.push(x);
};

/**
 * Removes the element on top of the stack and returns that element.
 * @return {number}
 */
MyStack.prototype.pop = function() {
    let size = this.queue.length;
    while (size-- > 1) {
        this.queue.push(this.queue.shift());
    }
    return this.queue.shift();
};

/**
 * Get the top element.
 * @return {number}
 */
MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue.push(x);
    return x;
};

/**
 * Returns whether the stack is empty.
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    return !this.queue.length;
};

TypeScript:

Version One: Using Two Queues to Simulate Stack

class MyStack {
    private queue: number[];
    private tempQueue: number[];
    constructor() {
        this.queue = [];
        this.tempQueue = [];
    }

    push(x: number): void {
        this.queue.push(x);
    }

    pop(): number {
        for (let i = 0, length = this.queue.length - 1; i < length; i++) {
            this.tempQueue.push(this.queue.shift()!);
        }
        let res: number = this.queue.pop()!;
        let temp: number[] = this.queue;
        this.queue = this.tempQueue;
        this.tempQueue = temp;
        return res;
    }

    top(): number {
        let res: number = this.pop();
        this.push(res);
        return res;
    }

    empty(): boolean {
        return this.queue.length === 0;
    }
}

Version Two: Using a Single Queue

class MyStack {
    private queue: number[];
    constructor() {
        this.queue = [];
    }

    push(x: number): void {
        this.queue.push(x);
    }

    pop(): number {
        for (let i = 0, length = this.queue.length - 1; i < length; i++) {
            this.queue.push(this.queue.shift()!);
        }
        return this.queue.shift()!;
    }

    top(): number {
        let res: number = this.pop();
        this.push(res);
        return res;
    }

    empty(): boolean {
        return this.queue.length === 0;
    }
}

Swift:

// Define a queue data structure
class Queue {
    var array: [Int]
    init() {
        array = [Int]()
    }
    
    /** Push element x to the back of queue. */
    func push(_ x: Int) {
        array.append(x)
    }
    
    /** Removes the element from in front of queue and returns that element. */
    func pop() -> Int {
        if array.isEmpty {
            return -1
        }
        return array.removeFirst()
    }
    
    /** Get the front element. */
    func peek() -> Int {
        if array.isEmpty {
            return -1
        }
        return array.first!
    }
    
    /** Returns whether the queue is empty. */
    func empty() -> Bool {
        return array.isEmpty
    }
    
    func count() -> Int {
        return array.count
    }
}

// Using double queue
class MyStack {
    var queue1: Queue
    var queue2: Queue
    
    init() {
        queue1 = Queue()
        queue2 = Queue()
    }
    
    func push(_ x: Int) {
        queue1.push(x)
    }
    
    func pop() -> Int {
        if queue1.empty() {
            return -1
        }
        while queue1.count() > 1 {
            queue2.push(queue1.pop())
        }
        let res = queue1.pop()
        while !queue2.empty() {
            queue1.push(queue2.pop())
        }
        return res
    }
    
    func top() -> Int {
        if queue1.empty() {
            return -1
        }
        let res = pop()
        push(res)
        return res
    }
    
    func empty() -> Bool {
        return queue1.empty() && queue2.empty()
    }
}

// Using a single queue
class MyStack {
    var queue: Queue
    
    init() {
        queue = Queue()
    }
    
    func push(_ x: Int) {
        queue.push(x)
    }
    
    func pop() -> Int {
        if queue.empty() {
            return -1
        }
        for _ in 1 ..< queue.count() {
            queue.push(queue.pop())
        }
        return queue.pop()
    }
    
    func top() -> Int {
        if queue.empty() {
            return -1
        }
        let res = pop()
        push(res)
        return res
    }
    
    func empty() -> Bool {
        return queue.empty()
    }
}

Scala:

Using Two Queues to Simulate Stack

import scala.collection.mutable

class MyStack() {

  val queue1 = new mutable.Queue[Int]()
  val queue2 = new mutable.Queue[Int]()

  def push(x: Int) {
    queue1.enqueue(x)
  }

  def pop(): Int = {
    var size = queue1.size
    // Transfer every element in queue1 to queue2
    for (i <- 0 until size - 1) {
      queue2.enqueue(queue1.dequeue())
    }
    var res = queue1.dequeue()
    // Transfer every element in queue2 back to queue1
    while (!queue2.isEmpty) {
      queue1.enqueue(queue2.dequeue())
    }
    res
  }

  def top(): Int = {
    var size = queue1.size
    for (i <- 0 until size - 1) {
      queue2.enqueue(queue1.dequeue())
    }
    var res = queue1.dequeue()
    while (!queue2.isEmpty) {
      queue1.enqueue(queue2.dequeue())
    }
    // Finally, push res back into queue1
    queue1.enqueue(res)
    res
  }

  def empty(): Boolean = {
    queue1.isEmpty
  }
}

Single Queue Simulation

import scala.collection.mutable

class MyStack() {

  val queue = new mutable.Queue[Int]()

  def push(x: Int) {
    queue.enqueue(x)
  }

  def pop(): Int = {
    var size = queue.size
    for (i <- 0 until size - 1) {
      queue.enqueue(queue.head) // Add the head to the tail of the queue
      queue.dequeue() // Then dequeue
    }
    queue.dequeue()
  }

  def top(): Int = {
    var size = queue.size
    var res = 0
    for (i <- 0 until size) {
      queue.enqueue(queue.head) // Add the head to the tail of the queue
      res = queue.dequeue() // Then dequeue
    }
    res
  }

  def empty(): Boolean = {
    queue.isEmpty
  }
}

C#:

Using Two Queues

public class MyStack {
    Queue<int> queue1;
    Queue<int> queue2;
    public MyStack() {
        queue1 = new Queue<int>();
        queue2 = new Queue<int>();
    }
    
    public void Push(int x) {
        queue2.Enqueue(x);
        while(queue1.Count != 0){
            queue2.Enqueue(queue1.Dequeue());
        }
        Queue<int> queueTemp;
        queueTemp = queue1;
        queue1 = queue2;
        queue2 = queueTemp;
    }
    
    public int Pop() {
        return queue1.Count > 0 ? queue1.Dequeue() : -1;
    }
    
    public int Top() {
        return queue1.Count > 0 ? queue1.Peek() : -1;
    }
    
    public bool Empty() {
        return queue1.Count == 0;
    }
}

Using a Single Queue

/*
 * @lc app=leetcode id=225 lang=csharp
 * Version Two: Single Queue
 * [225] Implement Stack using Queues
 */

// @lc code=start
public class MyStack {
    Queue<int> myQueue;
    public MyStack() {
        myQueue = new Queue<int>();
    }
    
    public void Push(int x) {
        myQueue.Enqueue(x);
    }
    
    // Implemented using a single queue
    public int Pop() {
        // To mimic stack pop, fetch the tail element
        for (var i = 0; i < myQueue.Count-1; i++)
        {
            myQueue.Enqueue(myQueue.Dequeue());
        }
        return myQueue.Dequeue();
    }

    // Reuse Pop method
    public int Top() {
        int res = Pop();
        myQueue.Enqueue(res);
        return res;
    }
    
    public bool Empty() {
        return (myQueue.Count == 0);
    }
}

// @lc code=end

PHP:

Using two queues

// SplQueue class provides basic queue functionalities through a doubly linked list (PHP 5 >= 5.3.0, PHP 7, PHP 8)
// https://www.php.net/manual/zh/class.splqueue.php
class MyStack {
    public $queueMain; // Holds data
    public $queueTmp;  // For auxiliary purposes

    function __construct() {
        $this->queueMain = new SplQueue();
        $this->queueTmp = new SplQueue();
    }
    
    // queueMain: 1,2,3 <= add
    function push($x) {
        $this->queueMain->enqueue($x);
    }
                                    
    function pop() {
       $qmSize = $this->queueMain->Count();
       $qmSize--;
       // queueMain: 3,2,1 => pop =>2,1 => add => 2,1 :queueTmp
       while ($qmSize--) {
           $this->queueTmp->enqueue($this->queueMain->dequeue());
       }
       // queueMain: 3
       $val = $this->queueMain->dequeue();
       // queueMain <= queueTmp 
       $this->queueMain = $this->queueTmp;
       // Clear queueTmp for next use
       $this->queueTmp = new SplQueue();
       return $val;
    }

    function top() {
        // Implemented using a doubly linked list: view the node from the end
        return $this->queueMain->top(); 
    }

    function empty() {
        return $this->queueMain->isEmpty();
    }
}

Using a single queue

class MyStack {
    public $queue;

    function __construct() {
        $this->queue = new SplQueue();
    }
    
    function push($x) {
        $this->queue->enqueue($x);
    }
                                 
    function pop() {
       $qmSize = $this->queue->Count();
       $qmSize--;
       // queue: 3,2,1 => pop =>2,1 => add => 2,1,3 :queue
       while ($qmSize--) {
           $this->queue->enqueue($this->queue->dequeue());
       }
       $val = $this->queue->dequeue();
       return $val;
    }

    function top() {
        return $this->queue->top(); 
    }

    function empty() {
        return $this->queue->isEmpty();
    }
}

Rust:

Rust Single Queue Solution

struct MyStack {
    queue: Vec<i32>,
}

impl MyStack {
    fn new() -> Self {
        MyStack { queue: vec![] }
    }

    fn push(&mut self, x: i32) {
        self.queue.push(x);
    }

    fn pop(&mut self) -> i32 {
        let len = self.queue.len() - 1;
        for _ in 0..len {
            let tmp = self.queue.remove(0);
            self.queue.push(tmp);
        }
        self.queue.remove(0)
    }

    fn top(&mut self) -> i32 {
        let res = self.pop();
        self.queue.push(res);
        res
    }

    fn empty(&self) -> bool {
        self.queue.is_empty()
    }
}

C:

Single Queue in C

typedef struct Node {
    int val;
    struct Node *next;
} Node_t;

// Implement queue using a single-linked list
typedef struct {
    Node_t *head;
    Node_t *foot;
    int size;
} MyStack;

MyStack* myStackCreate() {
    MyStack *obj = (MyStack *)malloc(sizeof(MyStack));
    assert(obj);
    obj->head = NULL;
    obj->foot = NULL;
    obj->size = 0;
    return obj;
}

void myStackPush(MyStack* obj, int x) {
    Node_t *temp = (Node_t *)malloc(sizeof(Node_t));
    assert(temp);
    temp->val = x;
    temp->next = NULL;

    // Add to the end of the queue
    if (obj->foot) {
        obj->foot->next = temp;
    } else {
        obj->head = temp;
    }
    obj->foot = temp;
    obj->size++;
}

int myStackPop(MyStack* obj) {
    // Get the last element
    int target = obj->foot->val;

    if (obj->head == obj->foot) {
        free(obj->foot);
        obj->head = NULL;
        obj->foot = NULL;
    } else {
        Node_t *prev = obj->head;
        // Move to the second-last node in the queue
        while (prev->next != obj->foot) {
            prev = prev->next;
        }

        free(obj->foot);
        obj->foot = prev;
        obj->foot->next = NULL;
    }

    obj->size--;
    return target;
}

int myStackTop(MyStack* obj) {
    return obj->foot->val;
}

bool myStackEmpty(MyStack* obj) {
    return obj->size == 0;
}

void myStackFree(MyStack* obj) {
    Node_t *curr = obj->head;
    while (curr != NULL) {
        Node_t *temp = curr->next;
        free(curr);
        curr = temp;
    }
    free(obj);
}