239. Sliding Window Maximum

LeetCode Problem Link (opens new window)

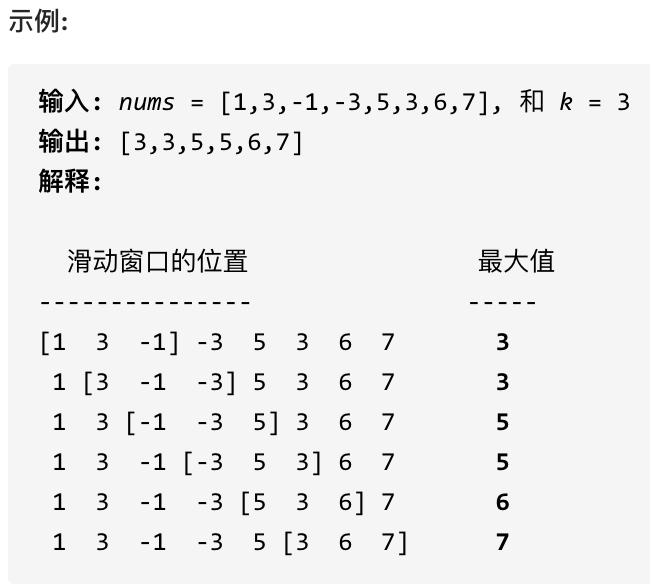
Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.

Return the maximum value in the sliding window.

Advanced:

Can you solve it in linear time complexity?

Constraints:

• 1 <= nums.length <= 10^5
• -10^4 <= nums[i] <= 10^4
• 1 <= k <= nums.length

Thought Process

This is a classic problem involving the use of a monotonic queue.

The tricky part is how to find the maximum value within a range of elements? A naive approach would be to traverse through the window and find the maximum value each time, which clearly results in a O(n × k) algorithm.

Some might think of using a max heap (priority queue) to maintain the k numbers in the window, so that we can quickly get the maximum value. However, the problem is that the window is moving, and a max heap only allows us to pop the maximum, not other values that need to be removed from the window. Therefore, a max heap isn't suitable in this case.

What we need is a queue that holds possible maximum values with each move of the window, maintaining this condition efficiently.

This queue should look like this:

class MyQueue {
public:
    void pop(int value) {
    }
    void push(int value) {
    }
    int front() {
        return que.front();
    }
};

Each time the window moves, we call que.pop(<element-outside-window>) and que.push(<new-element-in-window>), and then que.front() gives us the maximum value.

Such a data structure would be ideal, but what if we don't have one readily available?

Actually, in C++, we can use a multiset to simulate this process, although this simplification is specifically for C++. In the following discussion, let's focus on implementing our own monotonic queue.

If we consider the structure of this queue, the elements should be sorted, with the maximum placed at the exit. Otherwise, how could we determine the maximum value?

Yet, if the queue holds all elements within the window and the window slides, any removed element isn't necessarily the maximum value, which complicates the process for sorted queues.

We only need the queue to hold elements that may become the maximum value within the window, keeping them in decreasing order.

Such a decreasing order queue is known as a monotonic queue. C++ doesn't directly support monotonic queues, so we need to implement them ourselves.

Don't assume that implementing a monotonic queue involves sorting the window's elements; if that were the case, it would serve the same purpose as a priority queue.

Let's analyze how a monotonic queue maintains its elements.

The animation below illustrates this process:

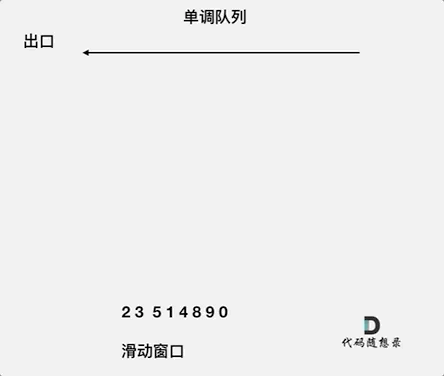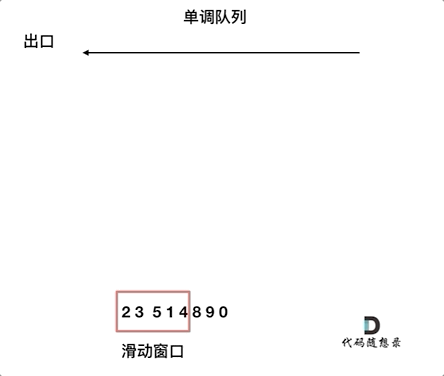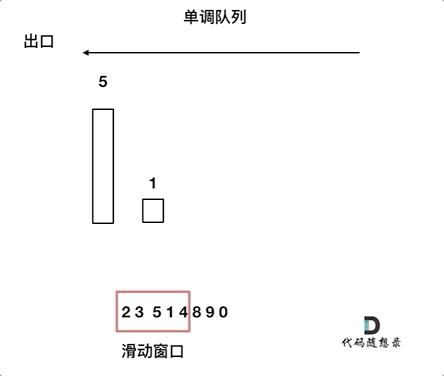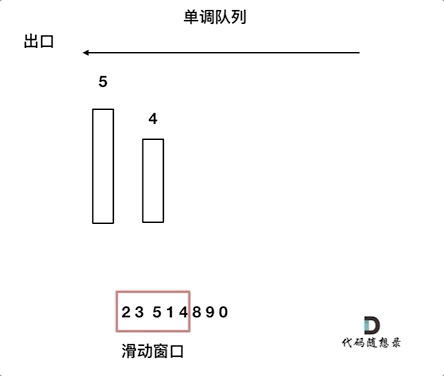
For the window containing elements {2, 3, 5, 1, 4}, only {5, 4} need to be maintained in the queue to ensure it is in non-increasing order, where the front of the queue is the maximum value of the window.

At this point, you may wonder how to handle the sliding of the window with a queue that maintains only {5, 4}.

Here's how the pop and push operations should follow the rules in our custom monotonic queue:

1. pop(value): If the element value to be removed due to the sliding window is equal to the front of the queue, then dequeue it. Otherwise, do nothing.
2. push(value): If value is greater than the tail element’s value in the queue, keep dequeuing the tail element until the value is less than or equal to the element at the tail of the queue.

Following these rules, with every move of the window, que.front() will give the current maximum value.

To better understand the function of a monotonic queue, consider the example given in the problem: nums = [1,3,-1,-3,5,3,6,7], and k = 3, with the animation below:

Which data structure should we use to construct this monotonic queue?

Using a deque is the most suitable option. In the Stack and Queue Fundamentals (opens new window), we discussed that the default underlying container for queue in C++ is a deque.

Based on the rules set for popping and pushing in the monotonic queue, implementing the code is not difficult:

class MyQueue { // Monotonic Queue (decreasing order)
public:
    deque<int> que; // Implementing monotonic queue using deque
    void pop(int value) {
        if (!que.empty() && value == que.front()) {
            que.pop_front();
        }
    }
    void push(int value) {
        while (!que.empty() && value > que.back()) {
            que.pop_back();
        }
        que.push_back(value);
    }
    int front() {
        return que.front();
    }
};

Now with a deque-implemented monotonic queue, solving the sliding window maximum problem is straightforward. Let's look at the code:

class Solution {
private:
    class MyQueue { // Monotonic Queue (decreasing order)
    public:
        deque<int> que; // Implementing monotonic queue using deque
        void pop(int value) {
            if (!que.empty() && value == que.front()) {
                que.pop_front();
            }
        }
        void push(int value) {
            while (!que.empty() && value > que.back()) {
                que.pop_back();
            }
            que.push_back(value);
        }
        int front() {
            return que.front();
        }
    };
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        MyQueue que;
        vector<int> result;
        for (int i = 0; i < k; i++) {
            que.push(nums[i]);
        }
        result.push_back(que.front());
        for (int i = k; i < nums.size(); i++) {
            que.pop(nums[i - k]);
            que.push(nums[i]);
            result.push_back(que.front());
        }
        return result;
    }
};

• Time Complexity: O(n)
• Space Complexity: O(k)

For the time complexity, using a monotonic queue is O(n).

Some may think the pop operation during a push could affect the complexity. However, observe that each element in nums can only be push_back and pop_back once, resulting in no redundant operations, thus maintaining the overall complexity of O(n).

The space complexity is O(k) because of the auxiliary queue.

Extensions

There seems to be some confusion about monotonic queues. It's crucial to understand that the pop and push interfaces of the monotonic queue in this solution are tailored for this problem. A monotonic queue isn't a one-size-fits-all solution; it varies in implementation based on different scenarios. The overarching aim is to maintain a monotonic order.

Similarly, some may question the deque in C++. Recall that we previously mentioned that stacks and queues default to using deque as their underlying implementation. The deque allows expansion at both ends, with non-consecutive element distribution.

Other Language Versions

Java:

//Solution One
//Custom Array
class MyQueue {
    Deque<Integer> deque = new LinkedList<>();
    void poll(int val) {
        if (!deque.isEmpty() && val == deque.peek()) {
            deque.poll();
        }
    }
    void add(int val) {
        while (!deque.isEmpty() && val > deque.getLast()) {
            deque.removeLast();
        }
        deque.add(val);
    }
    int peek() {
        return deque.peek();
    }
}

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 1) {
            return nums;
        }
        int len = nums.length - k + 1;
        int[] res = new int[len];
        int num = 0;
        MyQueue myQueue = new MyQueue();
        for (int i = 0; i < k; i++) {
            myQueue.add(nums[i]);
        }
        res[num++] = myQueue.peek();
        for (int i = k; i < nums.length; i++) {
            myQueue.poll(nums[i - k]);
            myQueue.add(nums[i]);
            res[num++] = myQueue.peek();
        }
        return res;
    }
}

//Solution Two
//Using Deque to Implement Monotonic Queue Manually
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        ArrayDeque<Integer> deque = new ArrayDeque<>();
        int n = nums.length;
        int[] res = new int[n - k + 1];
        int idx = 0;
        for(int i = 0; i < n; i++) {
            while(!deque.isEmpty() && deque.peek() < i - k + 1){
                deque.poll();
            }
            while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
                deque.pollLast();
            }

            deque.offer(i);

            if(i >= k - 1){
                res[idx++] = nums[deque.peek()];
            }
        }
        return res;
    }
}

Python:

Solution One: Using Custom Monotonic Queue Class

from collections import deque


class MyQueue: # Monotonic Queue (decreasing order)
    def __init__(self):
        self.queue = deque() # Use deque for monotonic queue since list times out
    
    def pop(self, value):
        if self.queue and value == self.queue[0]:
            self.queue.popleft() # list.pop() is O(n); hence, use collections.deque
            
    def push(self, value):
        while self.queue and value > self.queue[-1]:
            self.queue.pop()
        self.queue.append(value)
        
    def front(self):
        return self.queue[0]
    
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        que = MyQueue()
        result = []
        for i in range(k): # First put the first k elements in the queue
            que.push(nums[i])
        result.append(que.front()) # Record the maximum value of the first k elements
        for i in range(k, len(nums)):
            que.pop(nums[i - k]) # The sliding window removes the front element
            que.push(nums[i]) # The sliding window adds the rear element
            result.append(que.front()) # Record corresponding maximum
        return result

Solution Two: Directly Using Monotonic Queue

from collections import deque
class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        max_list = [] # Result list
        kept_nums = deque() # Monotonic queue

        for i in range(len(nums)):
            update_kept_nums(kept_nums, nums[i]) # Add new element on right

            if i >= k and nums[i - k] == kept_nums[0]: # Remove the head element if it equals the deque's front
                kept_nums.popleft()

            if i >= k - 1:
                max_list.append(kept_nums[0])

        return max_list

def update_kept_nums(kept_nums, num): # num is the newly added element
    # Remove all smaller elements from the tail since num is the new element
    while kept_nums and num > kept_nums[-1]:
        kept_nums.pop()

    kept_nums.append(num)

Go:

// Solution with Monotonic Queue encapsulation
type MyQueue struct {
    queue []int
}

func NewMyQueue() *MyQueue {
    return &MyQueue{
        queue: make([]int, 0),
    }
}

func (m *MyQueue) Front() int {
    return m.queue[0]
}

func (m *MyQueue) Back() int {
    return m.queue[len(m.queue)-1]
}

func (m *MyQueue) Empty() bool {
    return len(m.queue) == 0
}

func (m *MyQueue) Push(val int) {
    for !m.Empty() && val > m.Back() {
        m.queue = m.queue[:len(m.queue)-1]
    }
    m.queue = append(m.queue, val)
}

func (m *MyQueue) Pop(val int) {
    if !m.Empty() && val == m.Front() {
        m.queue = m.queue[1:]
    }
}

func maxSlidingWindow(nums []int, k int) []int {
    queue := NewMyQueue()
    length := len(nums)
    res := make([]int, 0)
    for i := 0; i < k; i++ {
        queue.Push(nums[i])
    }
    res = append(res, queue.Front())

    for i := k; i < length; i++ {
        queue.Pop(nums[i-k])
        queue.Push(nums[i])
        res = append(res, queue.Front())
    }
    return res
}

JavaScript:

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var maxSlidingWindow = function (nums, k) {
    class MonoQueue {
        queue;
        constructor() {
            this.queue = [];
        }
        enqueue(value) {
            let back = this.queue[this.queue.length - 1];
            while (back !== undefined && back < value) {
                this.queue.pop();
                back = this.queue[this.queue.length - 1];
            }
            this.queue.push(value);
        }
        dequeue(value) {
            let front = this.front();
            if (front === value) {
                this.queue.shift();
            }
        }
        front() {
            return this.queue[0];
        }
    }
    let helperQueue = new MonoQueue();
    let i = 0, j = 0;
    let resArr = [];
    while (j < k) {
        helperQueue.enqueue(nums[j++]);
    }
    resArr.push(helperQueue.front());
    while (j < nums.length) {
        helperQueue.enqueue(nums[j]);
        helperQueue.dequeue(nums[i]);
        resArr.push(helperQueue.front());
        i++, j++;
    }
    return resArr;
};

TypeScript:

function maxSlidingWindow(nums: number[], k: number): number[] {
    /** Monotonic Decreasing Queue */
    class MonoQueue {
        private queue: number[];
        constructor() {
            this.queue = [];
        };
        public enqueue(value: number): void {
            let back: number | undefined = this.queue[this.queue.length - 1];
            while (back !== undefined && back < value) {
                this.queue.pop();
                back = this.queue[this.queue.length - 1];
            }
            this.queue.push(value);
        };
        public dequeue(value: number): void {
            let top: number | undefined = this.top();
            if (top !== undefined && top === value) {
                this.queue.shift();
            }
        }
        public top(): number | undefined {
            return this.queue[0];
        }
    }
    const helperQueue: MonoQueue = new MonoQueue();
    let i: number = 0,
        j: number = 0;
    let resArr: number[] = [];
    while (j < k) {
        helperQueue.enqueue(nums[j++]);
    }
    resArr.push(helperQueue.top()!);
    while (j < nums.length) {
        helperQueue.enqueue(nums[j]);
        helperQueue.dequeue(nums[i]);
        resArr.push(helperQueue.top()!);
        j++, i++;
    }
    return resArr;
};

Swift:

Solution One:

/// Doubly Linked List
class DoublyListNode {
    var head: DoublyListNode?
    var tail: DoublyListNode?
    var next: DoublyListNode?
    var pre: DoublyListNode?
    var value: Int = 0
    init(_ value: Int = 0) {
        self.value = value
    }
    func isEmpty() -> Bool {
        return self.head == nil
    }
    func first() -> Int? {
        return self.head?.value
    }
    func last() -> Int? {
        return self.tail?.value
    }
    func removeFirst() {
        if isEmpty() {
            return
        }
        let next = self.head!.next
        self.head?.next = nil // Remove head
        next?.pre = nil
        self.head = next
    }
    func removeLast() {
        if let tail = self.tail {
            if let pre = tail.pre {
                self.tail?.pre = nil
                pre.next = nil
                self.tail = pre
            } else {
                self.head = nil
                self.tail = nil
            }
        }
    }
    func append(_ value: Int) {
        let node = DoublyListNode(value)
        if self.head != nil {
            node.pre = self.tail
            self.tail?.next = node
            self.tail = node
        } else {
            self.head = node
            self.tail = node
            self.pre = nil
            self.next = nil
        }
    }
}
// Monotonic Queue, decreasing order
class MyQueue {
//    var queue: [Int]! // List implementation times out
    var queue: DoublyListNode!
    init() {
//        queue = [Int]()
        queue = DoublyListNode()
    }
    // Pop the first element when sliding, only if equal
    func pop(x: Int) {
        if !queue.isEmpty() && front() == x {
            queue.removeFirst()
        }
    }
    // Add next element during slide, keep removal until head is greater
    func push(x: Int) {
        while !queue.isEmpty() && queue.last()! < x {
            queue.removeLast()
        }
        queue.append(x)
    }
    // Current queue's head is the max in sliding window
    func front() -> Int {
        return queue.first() ?? -1
    }
}

class Solution {
    func maxSlidingWindow(_ nums: [Int], _ k: Int) -> [Int] {
        // To store results
        var res = [Int]()
        let queue = MyQueue()
        // Place first K elements in the queue
        for i in 0 ..< k {
            queue.push(x: nums[i])
        }
        // Append the first K elements' maximum to the result
        res.append(queue.front())
        for i in k ..< nums.count {
            // Sliding window removes the first element
            queue.pop(x: nums[i - k])
            // Sliding window adds the next element
            queue.push(x: nums[i])
            // Store current queue's max
            res.append(queue.front())
        }
        return res
    }
}

Swift Solution Two:

func maxSlidingWindow(_ nums: [Int], _ k: Int) -> [Int] {
    var result = [Int]()
    var window = [Int]()
    var right = 0, left = right - k + 1

    while right < nums.count {
        let value = nums[right]

        // Remove the number left from the window
        if left > 0, left - 1 == window.first {
            window.removeFirst()
        }

        // Maintain monotonicity by removing all smaller elements from the tail
        while !window.isEmpty, value > nums[window.last!] {
            window.removeLast()
        }
        window.append(right)

        if left >= 0 { // When the window is formed
            result.append(nums[window.first!])
        }

        right += 1
        left += 1
    }

    return result
}

Scala:

import scala.collection.mutable.ArrayBuffer
object Solution {
  def maxSlidingWindow(nums: Array[Int], k: Int): Array[Int] = {
    var len = nums.length - k + 1   // Length of sliding window
    var res: Array[Int] = new Array[Int](len)   // Declare result array
    var index = 0   // Result array pointer
    val queue: MyQueue = new MyQueue    // Custom queue
    // Add first k elements to queue
    for (i <- 0 until k) {
      queue.add(nums(i))
    }
    res(index) = queue.peek // Max value of first sliding window
    index += 1
    for (i <- k until nums.length) {
      queue.poll(nums(i - k))   // Remove i-k th element first
      queue.add(nums(i))        // Add current number to queue
      res(index) = queue.peek() // Assign value
      index+=1
    }
    res // Return res, return keyword is optional
  }
 }

class MyQueue {
  var queue = ArrayBuffer[Int]()

  // Remove element, only if it equals the queue head
  def poll(value: Int): Unit = {
    if (!queue.isEmpty && queue.head == value) {
      queue.remove(0)
    }
  }

  // Add element, removing from the tail if larger
  def add(value: Int): Unit = {
    while (!queue.isEmpty && value > queue.last) {
      queue.remove(queue.length - 1)
    }
    queue.append(value)
  }

  def peek(): Int = queue.head
}

PHP:

class Solution {
    /**
     * @param Integer[] $nums
     * @param Integer $k
     * @return Integer[]
     */
    function maxSlidingWindow($nums, $k) {
        $myQueue = new MyQueue();
        for ($i = 0; $i < $k; $i++) { 
            $myQueue->push($nums[$i]);
        }

        $result = [];
        $result[] = $myQueue->max(); // Record the maximum value of the first k elements

        for ($i = $k; $i < count($nums); $i++) {
            $myQueue->pop($nums[$i - $k]); // The sliding window removes the front element
            $myQueue->push($nums[$i]); // The sliding window adds the rear element
            $result[]= $myQueue->max(); // Record corresponding maximum
        }
        return $result;
    }

}

// Constructing the monotonic queue
class MyQueue{
    private $queue;

    public function __construct(){
        $this->queue = new SplQueue(); // Double-ended linked list implementation.
    }

    public function pop($v){
        if(!$this->queue->isEmpty() && $v == $this->queue->bottom()){
            $this->queue->dequeue(); // Dequeue
        }
    }

    public function push($v){
        while (!$this->queue->isEmpty() && $v > $this->queue->top()) {
            $this->queue->pop(); // Pop from end
        }
        $this->queue->enqueue($v);
    }

    public function max(){
        return $this->queue->bottom(); 
    }

    public function println(){
        $this->queue->rewind();

        echo "Println: ";
        while($this->queue->valid()){
            echo $this->queue->current()," -> ";
            $this->queue->next();
        }
        echo "\n";
    } 
}

C#:

class myDequeue{
    private LinkedList<int> linkedList = new LinkedList<int>();

    public void Enqueue(int n){
        while(linkedList.Count > 0 && linkedList.Last.Value < n){
            linkedList.RemoveLast();
        }
        linkedList.AddLast(n);
    }

    public int Max(){
        return linkedList.First.Value;
    }

    public void Dequeue(int n){
        if(linkedList.First.Value == n){
            linkedList.RemoveFirst();
        }   
    }
}

myDequeue window = new myDequeue();
List<int> res = new List<int>();

public int[] MaxSlidingWindow(int[] nums, int k) {
    for(int i = 0; i < k; i++){
        window.Enqueue(nums[i]);
    }
    res.Add(window.Max());
    for(int i = k; i < nums.Length; i++){
        window.Dequeue(nums[i-k]);
        window.Enqueue(nums[i]);
        res.Add(window.Max());
    }

    return res.ToArray();
}

Rust:

impl Solution {
    pub fn max_sliding_window(nums: Vec<i32>, k: i32) -> Vec<i32> {
        let mut res = vec![];
        let mut queue = VecDeque::with_capacity(k as usize);
        for (i, &v) in nums.iter().enumerate() {
            if i - queue.front().unwrap_or(&0) == k as usize {
                queue.pop_front();
            }
            while let Some(&index) = queue.back() {
                if nums[index] >= v {
                    break;
                }
                queue.pop_back();
            }
            queue.push_back(i);
            if i >= k as usize - 1 {
                res.push(nums[queue[0]]);
            }
        }
        res
    }
}

C++

Using multiset as a Monotonic Queue

A multiset is a container which stores elements in a specific order, allowing duplicate values.

While traversing the original array, simply add the head element of the window to the multiset, and remove the tail element. As the multiset is ordered and provides *rbegin(), the maximum value in the window can be obtained directly.

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        multiset<int> st;
        vector<int> ans;
        for (int i = 0; i < nums.size(); i++) {
            if (i >= k) st.erase(st.find(nums[i - k]));
            st.insert(nums[i]);
            if (i >= k - 1) ans.push_back(*st.rbegin());
        }
        return ans;
    }
};

C

int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize) {
    *returnSize = numsSize - k + 1;
    int *res = (int*)malloc((*returnSize) * sizeof(int));
    assert(res);
    int *deque = (int*)malloc(numsSize * sizeof(int));
    assert(deque);
    int front = 0, rear = 0, idx = 0;

    for (int i  = 0 ; i < numsSize ; i++) {
        while (front < rear && deque[front] <= i - k) {
            front++;
        }

        while (front < rear && nums[deque[rear - 1]] <= nums[i]) {
            rear--;
        }

        deque[rear++] = i;

        if (i >= k - 1) {
            res[idx++] = nums[deque[front]];
        }
    }       

    return res;
}