This is not just a good problem; it also showcases the computational thinking of computers.
# 150. Evaluate Reverse Polish Notation
LeetCode Problem Link (opens new window)
Evaluate the value of an arithmetic expression in Reverse Polish Notation.
Valid operators are +, -, *, and /. Each operand may be an integer or another expression in Reverse Polish Notation.
Note:
- Integer division should truncate toward zero.
- The given Reverse Polish expression is always valid. It means that the expression would always evaluate to a result, and there will not be any division by zero operations.
Example 1:
- Input:
["2", "1", "+", "3", "*"] - Output:
9 - Explanation: The expression is evaluated as
((2 + 1) * 3) = 9.
Example 2:
- Input:
["4", "13", "5", "/", "+"] - Output:
6 - Explanation: The expression is evaluated as
(4 + (13 / 5)) = 6.
Example 3:
Input:
["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]Output:
22Explanation: The expression is evaluated as:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5 = ((10 * (6 / (12 * -11))) + 17) + 5 = ((10 * (6 / -132)) + 17) + 5 = ((10 * 0) + 17) + 5 = (0 + 17) + 5 = 17 + 5 = 221
2
3
4
5
6
7
Reverse Polish Notation (RPN) is a postfix notation wherein operators follow their operands.
In regular notation, which is known as infix, operators are placed between operands, as in (1 + 2) * (3 + 4).
The equivalent expression in Reverse Polish Notation would be ((1 2 +) (3 4 +) *).
RPN has the following advantages:
- It eliminates the need for parentheses to dictate evaluation order, e.g., even in a flat expression like
1 2 + 3 4 + *, calculations are still conducted in the correct order. - It is stack-friendly for computers: numbers are pushed onto the stack, and operators then pop numbers from the stack for calculation, pushing the result back on.
# Thought Process
# Main Discussion
In the previous article 1047. Remove All Adjacent Duplicates In String (opens new window), it was mentioned that recursion is implemented using a stack.
Hence, in certain contexts a stack and recursion are interchangeable! This will be elaborated upon when binary trees are covered.
For this problem, note that the reverse Polish expression can be thought of as a post-order traversal of a binary tree. Treat operators as intermediate nodes and visualize the expression as a tree using post-order rules.
There is no need to solve this through a binary tree perspective. Knowing that an RPN is essentially a serialized tree in post-order form is sufficient.
This problem is about producing a result for each sub-expression and then using that result for further calculations, which is reminiscent of the adjacent character elimination process just like 1047. Remove All Adjacent Duplicates In String (opens new window).
Check out the animation for clarity:
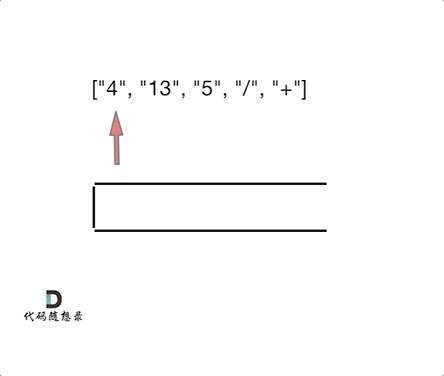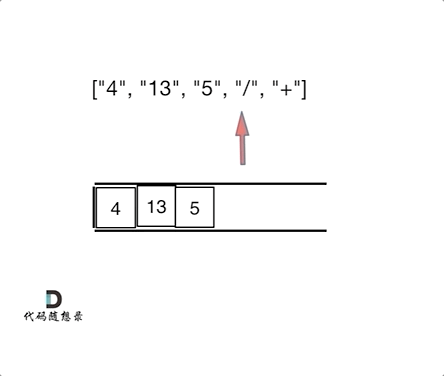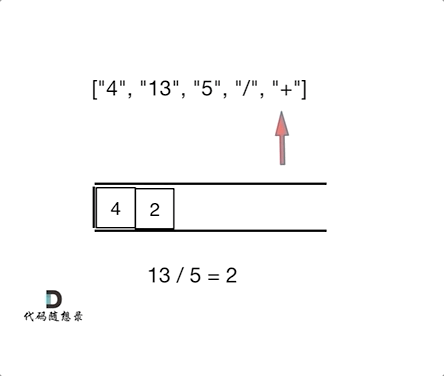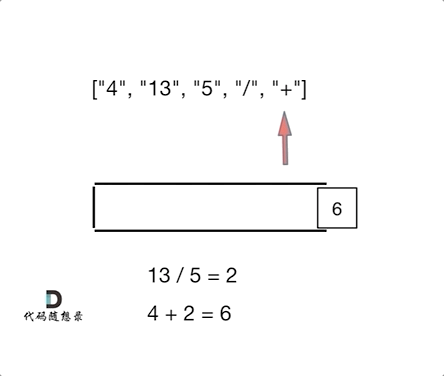
The animation should clarify that this problem resembles 1047. Remove All Adjacent Duplicates In String (opens new window); it's not about elimination, but execution of operations!
Here's the C++ code:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<long long> st;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
long long num1 = st.top();
st.pop();
long long num2 = st.top();
st.pop();
if (tokens[i] == "+") st.push(num2 + num1);
if (tokens[i] == "-") st.push(num2 - num1);
if (tokens[i] == "*") st.push(num2 * num1);
if (tokens[i] == "/") st.push(num2 / num1);
} else {
st.push(stoll(tokens[i]));
}
}
long long result = st.top();
st.pop();
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- Time Complexity:
O(n) - Space Complexity:
O(n)
# Additional Insights
We are familiar with infix expressions because it's what people naturally use, but infix is not very computer-friendly.
For instance, consider 4 + 13 / 5 as an infix expression. A computer reading left to right must still determine precedence and manage operands accordingly—jumping back to continue the overall calculation. Quite cumbersome indeed!
Conversely, the same expression in postfix i.e., ["4", "13", "5", "/", "+"] can be processed more straightforwardly using a stack, without precedence concerns or backtracking, making postfix much more efficient for computers.
This problem not only showcases a computational problem but also exemplifies how computers think and operate.
In the 1970s and 1980s, Hewlett-Packard utilized RPN in all their calculators and continued its use in some models into the 2020s.
Referencing Wikipedia:
During the 1970s and 1980s, Hewlett-Packard used RPN in all of their desktop and hand-held calculators, and continued to use it in some models into the 2020s.
# Solution in Other Languages
# Java:
class Solution {
public int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList();
for (String s : tokens) {
if ("+".equals(s)) {
stack.push(stack.pop() + stack.pop());
} else if ("-".equals(s)) {
stack.push(-stack.pop() + stack.pop());
} else if ("*".equals(s)) {
stack.push(stack.pop() * stack.pop());
} else if ("/".equals(s)) {
int temp1 = stack.pop();
int temp2 = stack.pop();
stack.push(temp2 / temp1);
} else {
stack.push(Integer.valueOf(s));
}
}
return stack.pop();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Python3:
from operator import add, sub, mul
def div(x, y):
return int(x / y) if x * y > 0 else -(abs(x) // abs(y))
class Solution(object):
op_map = {'+': add, '-': sub, '*': mul, '/': div}
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for token in tokens:
if token not in {'+', '-', '*', '/'}:
stack.append(int(token))
else:
op2 = stack.pop()
op1 = stack.pop()
stack.append(self.op_map[token](op1, op2))
return stack.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Another approach involving eval() (slower):
class Solution(object):
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for token in tokens:
if token.isdigit() or (len(token) > 1 and token[1:].isdigit()):
stack.append(token)
else:
op2 = stack.pop()
op1 = stack.pop()
stack.append(str(int(eval(op1 + token + op2))))
return int(stack.pop())
2
3
4
5
6
7
8
9
10
11
# Go:
func evalRPN(tokens []string) int {
stack := []int{}
for _, token := range tokens {
val, err := strconv.Atoi(token)
if err == nil {
stack = append(stack, val)
} else {
num1, num2 := stack[len(stack)-2], stack[len(stack)-1]
stack = stack[:len(stack)-2]
switch token {
case "+":
stack = append(stack, num1+num2)
case "-":
stack = append(stack, num1-num2)
case "*":
stack = append(stack, num1*num2)
case "/":
stack = append(stack, num1/num2)
}
}
}
return stack[0]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# JavaScript:
var evalRPN = function (tokens) {
const stack = [];
for (const token of tokens) {
if (isNaN(Number(token))) {
const n2 = stack.pop();
const n1 = stack.pop();
switch (token) {
case "+":
stack.push(n1 + n2);
break;
case "-":
stack.push(n1 - n2);
break;
case "*":
stack.push(n1 * n2);
break;
case "/":
stack.push(n1 / n2 | 0);
break;
}
} else {
stack.push(Number(token));
}
}
return stack[0];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# TypeScript:
Basic Version:
function evalRPN(tokens: string[]): number {
let helperStack: number[] = [];
let temp: number;
let i: number = 0;
while (i < tokens.length) {
let t: string = tokens[i];
switch (t) {
case '+':
temp = helperStack.pop()! + helperStack.pop()!;
helperStack.push(temp);
break;
case '-':
temp = helperStack.pop()!;
temp = helperStack.pop()! - temp;
helperStack.push(temp);
break;
case '*':
temp = helperStack.pop()! * helperStack.pop()!;
helperStack.push(temp);
break;
case '/':
temp = helperStack.pop()!;
temp = Math.trunc(helperStack.pop()! / temp);
helperStack.push(temp);
break;
default:
helperStack.push(Number(t));
break;
}
i++;
}
return helperStack.pop()!;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Optimized Version:
function evalRPN(tokens: string[]): number {
const helperStack: number[] = [];
const operatorMap: Map<string, (a: number, b: number) => number> = new Map([
['+', (a, b) => a + b],
['-', (a, b) => a - b],
['/', (a, b) => Math.trunc(a / b)],
['*', (a, b) => a * b],
]);
let a: number, b: number;
for (let t of tokens) {
if (operatorMap.has(t)) {
b = helperStack.pop()!;
a = helperStack.pop()!;
helperStack.push(operatorMap.get(t)!(a, b));
} else {
helperStack.push(Number(t));
}
}
return helperStack.pop()!;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Swift:
func evalRPN(_ tokens: [String]) -> Int {
var stack = [Int]()
for c in tokens {
let v = Int(c)
if let num = v {
stack.append(num)
} else {
var res: Int = 0
let num2 = stack.popLast()!
let num1 = stack.popLast()!
switch c {
case "+":
res = num1 + num2
case "-":
res = num1 - num2
case "*":
res = num1 * num2
case "/":
res = num1 / num2
default:
break
}
stack.append(res)
}
}
return stack.last!
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# C#:
public int EvalRPN(string[] tokens) {
int num;
Stack<int> stack = new Stack<int>();
foreach(string s in tokens){
if(int.TryParse(s, out num)){
stack.Push(num);
}else{
int num1 = stack.Pop();
int num2 = stack.Pop();
switch (s)
{
case "+":
stack.Push(num1 + num2);
break;
case "-":
stack.Push(num2 - num1);
break;
case "*":
stack.Push(num1 * num2);
break;
case "/":
stack.Push(num2 / num1);
break;
default:
break;
}
}
}
return stack.Pop();
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# PHP:
class Solution {
function evalRPN($tokens) {
$st = new SplStack();
for($i = 0;$i<count($tokens);$i++){
if(is_numeric($tokens[$i])){
$st->push($tokens[$i]);
}else{
$num1 = $st->pop();
$num2 = $st->pop();
if ($tokens[$i] == "+") $st->push($num2 + $num1);
if ($tokens[$i] == "-") $st->push($num2 - $num1);
if ($tokens[$i] == "*") $st->push($num2 * $num1);
if ($tokens[$i] == "/") $st->push(intval($num2 / $num1));
}
}
return $st->pop();
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Scala:
object Solution {
import scala.collection.mutable
def evalRPN(tokens: Array[String]): Int = {
val stack = mutable.Stack[Int]()
def operator(x: Int, y: Int, f: (Int, Int) => Int): Int = f(x, y)
for (token <- tokens) {
token match {
case "+" => stack.push(operator(stack.pop(), stack.pop(), _ + _))
case "-" => stack.push(operator(stack.pop(), stack.pop(), -_ + _))
case "*" => stack.push(operator(stack.pop(), stack.pop(), _ * _))
case "/" => {
var pop1 = stack.pop()
var pop2 = stack.pop()
stack.push(operator(pop2, pop1, _ / _))
}
case _ => stack.push(token.toInt)
}
}
stack.pop()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Rust:
impl Solution {
pub fn eval_rpn(tokens: Vec<String>) -> i32 {
let mut stack = vec![];
for token in tokens.into_iter() {
match token.as_str() {
"+" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() += a;
}
"-" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() -= a;
}
"*" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() *= a;
}
"/" => {
let a = stack.pop().unwrap();
*stack.last_mut().unwrap() /= a;
}
_ => {
stack.push(token.parse::<i32>().unwrap());
}
}
}
stack.pop().unwrap()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# C:
int str_to_int(char *str) {
int num = 0, tens = 1;
for (int i = strlen(str) - 1; i >= 0; i--) {
if (str[i] == '-') {
num *= -1;
break;
}
num += (str[i] - '0') * tens;
tens *= 10;
}
return num;
}
int evalRPN(char** tokens, int tokensSize) {
int *stack = (int *)malloc(tokensSize * sizeof(int));
assert(stack);
int stackTop = 0;
for (int i = 0; i < tokensSize; i++) {
char symbol = (tokens[i])[0];
if (symbol < '0' && (tokens[i])[1] == '\0') {
int num1 = stack[--stackTop];
int num2 = stack[--stackTop];
int result;
if (symbol == '+') {
result = num1 + num2;
} else if (symbol == '-') {
result = num2 - num1;
} else if (symbol == '/') {
result = num2 / num1;
} else {
result = num1 * num2;
}
stack[stackTop++] = result;
} else {
int num = str_to_int(tokens[i]);
stack[stackTop++] = num;
}
}
int result = stack[0];
free(stack);
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
