# 129. Sum Root to Leaf Numbers
LeetCode Problem Link (opens new window)
# Approach
This problem shares a similar approach with 113. Path Sum II (opens new window). After completing this problem, you can also tackle 113. Path Sum II (opens new window) and 112. Path Sum (opens new window).
If you're unsure when a recursive function in a binary tree needs a return value, you might find it helpful to check Binary Tree: When Does a Recursive Function Need a Return Value and When Does It Not? (opens new window).
Once you understand these, this problem becomes much simpler. While addressing this problem, you will actually employ backtracking, though some might not realize they are using backtracking. In Binary Tree: Using Recursion and Discovering Hidden Backtracking (opens new window), I have explained in detail how backtracking is used within recursion in binary tree problems.
Now let's look at the problem:
The idea is clear: traverse the entire tree and sum up the numbers formed from the root node to each leaf node.
We begin by following the three-step approach of recursion:
# Three Steps of Recursion
If you are not familiar with these steps, you can refer to Binary Tree: Preorder, Inorder, and Postorder Traversal Explained (opens new window).
- Determine the return value and its parameters for the recursive function
Here, we need to traverse the entire binary tree and require a return value to handle logic, so the return type is void. This was discussed in detail in Binary Tree: When Does a Recursive Function Need a Return Value and When Does It Not? (opens new window).
The function should take the root node as its parameter. We also define two global variables, one for the result, and a vector<int> path.
Why use a vector type (array)? Because using a vector simplifies backtracking!
So the code is as follows:
int result;
vector<int> path;
void traversal(TreeNode* cur)
2
3
- Determine the termination condition
The recursion stops when we reach a leaf node. At this point, we collect the result and move back to the previous level of recursion. Since we're using a vector for a single path, we need a function vectorToInt to convert the vector to an integer.
The termination condition is coded as follows:
if (!cur->left && !cur->right) { // Leaf node reached
result += vectorToInt(path);
return;
}
2
3
4
Here, the vectorToInt function converts the vector to an integer, as shown below:
int vectorToInt(const vector<int>& vec) {
int sum = 0;
for (int i = 0; i < vec.size(); i++) {
sum = sum * 10 + vec[i];
}
return sum;
}
2
3
4
5
6
7
- Determine the single-layer recursive logic
For this problem, it does not matter whether you use preorder, inorder, or postorder traversal, as there is no specific logic to handle for intermediate nodes.
The key point is that when the left node is not null, you record the path and recursively traverse the left child, and similarly for the right node.
And don't forget to backtrack.
Refer to the illustration:
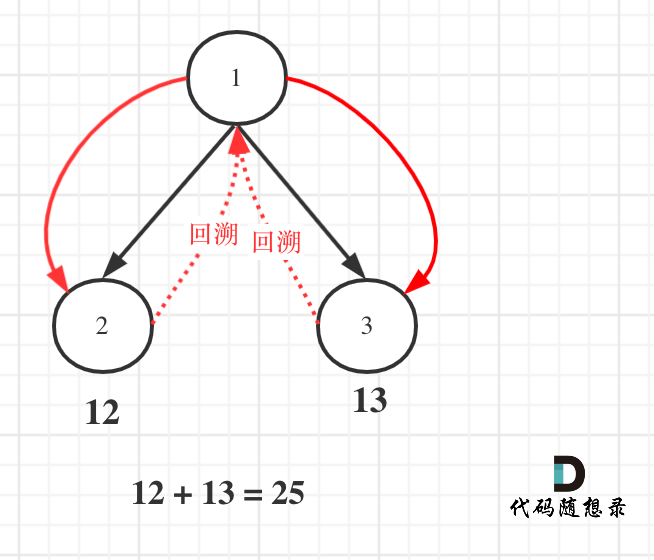
The code is as follows:
// Process current node
if (cur->left) { // Traverse left (excluding null nodes)
path.push_back(cur->left->val);
traversal(cur->left); // Recursion
path.pop_back(); // Backtracking
}
if (cur->right) { // Traverse right (excluding null nodes)
path.push_back(cur->right->val);
traversal(cur->right); // Recursion
path.pop_back(); // Backtracking
}
2
3
4
5
6
7
8
9
10
11
Note that the backtracking and recursion should always be together, a one-to-one relationship. Some might write the code as follows:
if (cur->left) { // Traverse left (excluding null nodes)
path.push_back(cur->left->val);
traversal(cur->left); // Recursion
}
if (cur->right) { // Traverse right (excluding null nodes)
path.push_back(cur->right->val);
traversal(cur->right); // Recursion
}
path.pop_back(); // Backtracking
2
3
4
5
6
7
8
9
Placing the backtracking step outside the braces is incorrect.
Complete C++ Code
With the key logic discussed, here is the complete C++ code:
class Solution {
private:
int result;
vector<int> path;
// Convert vector to int
int vectorToInt(const vector<int>& vec) {
int sum = 0;
for (int i = 0; i < vec.size(); i++) {
sum = sum * 10 + vec[i];
}
return sum;
}
void traversal(TreeNode* cur) {
if (!cur->left && !cur->right) { // Leaf node reached
result += vectorToInt(path);
return;
}
if (cur->left) { // Traverse left (excluding null nodes)
path.push_back(cur->left->val); // Process node
traversal(cur->left); // Recursion
path.pop_back(); // Backtracking, undo
}
if (cur->right) { // Traverse right (excluding null nodes)
path.push_back(cur->right->val); // Process node
traversal(cur->right); // Recursion
path.pop_back(); // Backtracking, undo
}
return;
}
public:
int sumNumbers(TreeNode* root) {
path.clear();
if (root == nullptr) return 0;
path.push_back(root->val);
traversal(root);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Summary
Overly simplified code can easily obscure the essence of backtracking in this problem, even to the point where the author might not realize they were using backtracking.
The code I provide fully incorporates the backtracking process, aiming to make this clear to everyone!
# Other Language Versions
# Java:
class Solution {
List<Integer> path = new ArrayList<>();
int res = 0;
public int sumNumbers(TreeNode root) {
// If the node is null, return 0
if (root == null) return 0;
// First, add the root node to the collection
path.add(root.val);
// Begin recursion
recur(root);
return res;
}
public void recur(TreeNode root){
if (root.left == null && root.right == null) {
// Process when it's a leaf node
res += listToInt(path);
return;
}
if (root.left != null){
// Note backtracking
path.add(root.left.val);
recur(root.left);
path.remove(path.size() - 1);
}
if (root.right != null){
// Note backtracking
path.add(root.right.val);
recur(root.right);
path.remove(path.size() - 1);
}
return;
}
public int listToInt(List<Integer> path){
int sum = 0;
for (Integer num:path){
// sum * 10 indicates a digit place
sum = sum * 10 + num;
}
return sum;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# Python:
class Solution:
def sumNumbers(self, root: TreeNode) -> int:
res = 0
path = []
def backtrace(root):
nonlocal res
if not root: return # If node is null, return
path.append(root.val)
if not root.left and not root.right: # Leaf node reached
res += get_sum(path)
if root.left: # If left subtree is not null
backtrace(root.left)
if root.right: # If right subtree is not null
backtrace(root.right)
path.pop()
def get_sum(arr):
s = 0
for i in range(len(arr)):
s = s * 10 + arr[i]
return s
backtrace(root)
return res
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Go:
func sumNumbers(root *TreeNode) int {
sum := 0
dfs(root, root.Val, &sum)
return sum
}
func dfs(root *TreeNode, tmpSum int, sum *int) {
if root.Left == nil && root.Right == nil {
*sum += tmpSum
} else {
if root.Left != nil {
dfs(root.Left, tmpSum*10 + root.Left.Val, sum)
}
if root.Right != nil {
dfs(root.Right, tmpSum*10 + root.Right.Val, sum)
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# JavaScript:
var sumNumbers = function(root) {
const listToInt = path => {
let sum = 0;
for(let num of path){
// sum * 10 indicates a digit place
sum = sum * 10 + num;
}
return sum;
}
const recur = root =>{
if (root.left == null && root.right == null) {
// Process when it's a leaf node
res += listToInt(path);
return;
}
if (root.left != null){
// Note backtracking
path.push(root.left.val);
recur(root.left);
path.pop();
}
if (root.right != null){
// Note backtracking
path.push(root.right.val);
recur(root.right);
path.pop();
}
return;
};
const path = new Array();
let res = 0;
// If the node is null, return 0
if (root == null) return 0;
// First, add the root node to the collection
path.push(root.val);
// Begin recursion
recur(root);
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# TypeScript:
function sumNumbers(root: TreeNode | null): number {
if (root === null) return 0;
// Record the final result
let resTotal: number = 0;
// Record the node values encountered on the path
const route: number[] = [];
// Initial value for recursion
route.push(root.val);
recur(root, route);
return resTotal;
function recur(node: TreeNode, route: number[]): void {
if (node.left === null && node.right === null) {
resTotal += listToSum(route);
return;
}
if (node.left !== null) {
route.push(node.left.val);
recur(node.left, route);
route.pop();
};
if (node.right !== null) {
route.push(node.right.val);
recur(node.right, route);
route.pop();
};
}
function listToSum(nums: number[]): number {
// Sum of the array
return Number(nums.join(''));
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# C:
//sum records the total
int sum;
void traverse(struct TreeNode *node, int val) {
// Update val as the sum from the root to the current node
val = val * 10 + node->val;
// If the current node is a leaf, record val
if(!node->left && !node->right) {
sum+=val;
return;
}
// If there is a left/right node, traverse left/right node
if(node->left)
traverse(node->left, val);
if(node->right)
traverse(node->right, val);
}
int sumNumbers(struct TreeNode* root){
sum = 0;
traverse(root, 0);
return sum;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
