5. Longest Palindromic Substring

LeetCode Problem Link (opens new window)

Given a string s, find the longest palindromic substring in s.

Example 1:

• Input: s = "babad"
• Output: "bab"
• Explanation: "aba" is also a valid answer.

Example 2:

• Input: s = "cbbd"
• Output: "bb"

Example 3:

• Input: s = "a"
• Output: "a"

Example 4:

• Input: s = "ac"
• Output: "a"

Approach

This problem is quite similar to 0647.Palindromic Substrings (opens new window), although 0647.Palindromic Substrings is a bit more fundamental. It is recommended to solve 0647.Palindromic Substrings first.

Brute Force Solution

Use two nested for loops to iterate over starting and ending positions of the interval, then check if this interval is a palindrome.

Time complexity: O(n^3)

Dynamic Programming

Dynamic Programming Steps:

1. Define the dp array (dp table) and meaning of the indices

A boolean dp[i][j]: Denotes whether the substring within the interval [i, j] (inclusive) is a palindromic substring. If it is, dp[i][j] is true; otherwise, it is false.

2. Determine the recurrence relation

When establishing the recurrence relation, certain cases must be analyzed.

Overall, there are two cases: s[i] is equal to s[j], and s[i] is not equal to s[j].

• If s[i] is not equal to s[j], dp[i][j] is certainly false.

• If s[i] is equal to s[j], the following conditions apply:

  • Case 1: i and j are the same, for instance a, which is certainly a palindromic substring
  • Case 2: i and j differ by 1, such as aa, which is also a palindromic substring
  • Case 3: i and j differ by more than 1, for instance cabac. Here, s[i] and s[j] are already equal, so to determine whether the interval [i, j] is palindromic, it relies on whether aba (specifically the interval from i+1 to j-1) is palindromic, looked at by whether dp[i+1][j-1] is true.

With the above analysis, the recursion formula becomes:

if (s[i] == s[j]) {
    if (j - i <= 1) { // Case 1 and Case 2
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // Case 3
        dp[i][j] = true;
    }
}

Note that we do not list the case where s[i] is not equal to s[j] because dp[i][j] is initially initialized to false below.

When the [i, j] interval is confirmed to be a palindromic substring, directly save the left and right boundaries of the longest palindromic substring:

if (s[i] == s[j]) {
    if (j - i <= 1) { // Case 1 and Case 2
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // Case 3
        dp[i][j] = true;
    }
}
if (dp[i][j] && j - i + 1 > maxLength) {
    maxLength = j - i + 1;
    left = i;
    right = j;
}

3. How to initialize the dp array

Is it possible to initialize dp[i][j] to true? Of course not, it would preemptively consider everything as matched.

So initialize dp[i][j] as false.

4. Determine the traversal order

The traversal order requires careful consideration.

Looking at the recurrence relation, Case 3 is based on whether dp[i + 1][j - 1] is true in order to assign true to dp[i][j].

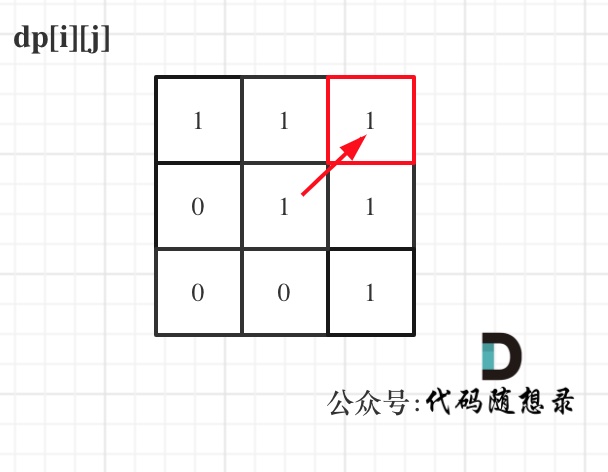
dp[i + 1][j - 1] is located at the lower left of dp[i][j], as shown:

If the matrix is traversed from top to bottom and from left to right, it would use dp[i + 1][j - 1] which hasn't been calculated. Essentially, it judges [i,j] based on an uncertain palindromic interval [i+1,j-1], leading to incorrect results.

Therefore, the traversal must be done bottom-to-top and left-to-right, ensuring that dp[i + 1][j - 1] has been calculated.

Some code implementations prioritize column traversal before row traversal, which serves the same purpose: ensuring dp[i + 1][j - 1] has been calculated.

The code is as follows:

for (int i = s.size() - 1; i >= 0; i--) { // Note the traversal order
    for (int j = i; j < s.size(); j++) {
        if (s[i] == s[j]) {
            if (j - i <= 1) { // Case 1 and Case 2
                dp[i][j] = true;
            } else if (dp[i + 1][j - 1]) { // Case 3
                dp[i][j] = true;
            }
        }
        if (dp[i][j] && j - i + 1 > maxLength) {
            maxLength = j - i + 1;
            left = i;
            right = j;
        }
    }
}

5. Run an example to deduce the dp array

Example input: "aaa", the state of dp[i][j] is as follows:

Note that because of the definition of dp[i][j], j is always greater than or equal to i. Thus, while filling dp[i][j], only the upper right half is filled.

Having completed the explanation, here is the C++ code:

class Solution {
public:
    string longestPalindrome(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        int maxLength = 0;
        int left = 0;
        int right = 0;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    if (j - i <= 1) { // Case 1 and Case 2
                        dp[i][j] = true;
                    } else if (dp[i + 1][j - 1]) { // Case 3
                        dp[i][j] = true;
                    }
                }
                if (dp[i][j] && j - i + 1 > maxLength) {
                    maxLength = j - i + 1;
                    left = i;
                    right = j;
                }
            }

        }
        return s.substr(left, right - left + 1);
    }
};

The above code highlights Cases 1, 2, and 3, but can be simplified:

class Solution {
public:
    string longestPalindrome(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        int maxLength = 0;
        int left = 0;
        int right = 0;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
                    dp[i][j] = true;
                }
                if (dp[i][j] && j - i + 1 > maxLength) {
                    maxLength = j - i + 1;
                    left = i;
                    right = j;
                }
            }
        }
        return s.substr(left, maxLength);
    }
};

• Time Complexity: O(n^2)
• Space Complexity: O(n^2)

Two Pointers

The space complexity of dynamic programming is on the higher side. Let's examine the two-pointer method.

To identify a palindromic substring, consider a center and expand outwards to check for symmetry.

When traversing to find center points, note there are two cases.

A single element can be a center and two elements can also be a center.

Some may ask, can't three elements be a center as well? Indeed, three elements can be reduced to a scenario with one element supplemented by elements on both sides, and similarly, four elements can be reduced to a scenario with two elements supplemented by elements on both sides.

Thus, when computing, attend to both a single element being a center and two elements being a center case.

These two cases can be calculated together but it's clearer to compute them separately, which I prefer, as shown in the following code:

class Solution {
public:
    int left = 0;
    int right = 0;
    int maxLength = 0;
    string longestPalindrome(string s) {
        int result = 0;
        for (int i = 0; i < s.size(); i++) {
            extend(s, i, i, s.size()); // Single character as center
            extend(s, i, i + 1, s.size()); // Two characters as center
        }
        return s.substr(left, maxLength);
    }
    void extend(const string& s, int i, int j, int n) {
        while (i >= 0 && j < n && s[i] == s[j]) {
            if (j - i + 1 > maxLength) {
                left = i;
                right = j;
                maxLength = j - i + 1;
            }
            i--;
            j++;
        }
    }
};

• Time Complexity: O(n^2)
• Space Complexity: O(1)

Manacher's Algorithm

The core of Manacher's algorithm lies in efficiently using the symmetry of palindromes. By inserting separators and maintaining information like center and boundaries, it finds the longest palindromic substring in linear time. This avoids unnecessary repeated calculations, providing an optimal solution for palindrome problems.

// Manacher's Algorithm
class Solution {
public:
    string longestPalindrome(string s) {
        string t = "#";
        for (char c : s) {
            t += c;
            t += '#';
        }
        int n = t.size();
        vector<int> p(n, 0);
        int center = 0, right = 0;

        for (int i = 0; i < n; i++) {
            if (i < right) {
                p[i] = min(right - i, p[2 * center - i]);
            }
            while (i - p[i] - 1 >= 0 && i + p[i] + 1 < n && t[i - p[i] - 1] == t[i + p[i] + 1]) {
                p[i]++;
            }
            if (i + p[i] > right) {
                center = i;
                right = i + p[i];
            }
        }
        int maxLen = 0, centerIndex = 0;
        for (int i = 0; i < n; i++) {
            if (p[i] > maxLen) {
                maxLen = p[i];
                centerIndex = i;
            }
        }
        return s.substr((centerIndex - maxLen) / 2, maxLen);
    }
};

• Time Complexity: O(n)
• Space Complexity: O(n)

Other Language Versions

Java:

// Two Pointers and Dynamic Programming
class Solution {
    public String longestPalindrome(String s) {
        if (s.length() == 0 || s.length() == 1) return s;
        int length = 1;
        int index = 0;
        boolean[][] palindrome = new boolean[s.length()][s.length()];
        for (int i = 0; i < s.length(); i++) {
            palindrome[i][i] = true;
        }

        for (int L = 2; L <= s.length(); L++) {
            for (int i = 0; i < s.length(); i++) {
                int j = i + L - 1;
                if (j >= s.length()) break;
                if (s.charAt(i) != s.charAt(j)) {
                    palindrome[i][j] = false;
                } else {
                    if (j - i < 3) {
                        palindrome[i][j] = true;
                    } else {
                        palindrome[i][j] = palindrome[i + 1][j - 1];
                    }
                }
                if (palindrome[i][j] && j - i + 1 > length) {
                    length = j - i + 1;
                    index = i;
                }
            }
        }
        return s.substring(index, index + length);
    }
}

// Two Pointers and Center Expansion
class Solution {
    public String longestPalindrome(String s) {
        String s1 = "";
        String s2 = "";
        String res = "";
        for (int i = 0; i < s.length(); i++) {
            s1 = extend(s, i, i);  // Single character as center
            res = s1.length() > res.length() ? s1 : res;
            s2 = extend(s, i, i + 1);  // Two characters as center
            res = s2.length() > res.length() ? s2 : res;
        }
        return res;
    }
    public String extend(String s, int start, int end){
        String tmp = "";
        while (start >= 0 && end < s.length() && s.charAt(start) == s.charAt(end)){
            tmp = s.substring(start, end + 1);
            start--;
            end++;
        }
        return tmp;
    }
}

Python:

# Dynamic Programming
class Solution:
    def longestPalindrome(self, s: str) -> str:
        dp = [[False] * len(s) for _ in range(len(s))]
        maxLength = 0
        left = 0
        right = 0
        for i in range(len(s) - 1, -1, -1):
            for j in range(i, len(s)):
                if s[j] == s[i]:
                    if j - i <= 1 or dp[i + 1][j - 1]:
                        dp[i][j] = True
                if dp[i][j] and j - i + 1 > maxLength:
                    maxLength = j - i + 1
                    left = i
                    right = j
        return s[left:right + 1]

Two Pointers:

# Two Pointers
class Solution:
    def longestPalindrome(self, s: str) -> str:

        def find_point(i, j, s):
            while i >= 0 and j < len(s) and s[i] == s[j]:
                i -= 1
                j += 1
            return i + 1, j

        def compare(start, end, left, right):
            if right - left > end - start:
                return left, right
            else:
                return start, end

        start = 0
        end = 0
        for i in range(len(s)):
            left, right = find_point(i, i, s)
            start, end = compare(start, end, left, right)

            left, right = find_point(i, i + 1, s)
            start, end = compare(start, end, left, right)
        return s[start:end]

Go:

// Dynamic Programming
func longestPalindrome(s string) string {
    maxLength := 0
    left := 0
    length := 0
    dp := make([][]bool, len(s))
    for i := 0; i < len(s); i++ {
        dp[i] = make([]bool, len(s))
    }
    for i := len(s) - 1; i >= 0; i-- {
        for j := i; j < len(s); j++ {
            if s[i] == s[j] {
                if j-i <= 1 { // Case 1 and Case 2
                    length = j - i
                    dp[i][j] = true
                } else if dp[i+1][j-1] { // Case 3
                    length = j - i
                    dp[i][j] = true
                }
            }
        }
        if length > maxLength {
            maxLength = length
            left = i
        }
    }
    return s[left : left+maxLength+1]
}

JavaScript:

// Dynamic Programming
const longestPalindrome = function(s) {
    const len = s.length;
    const dp = Array.from({ length: len }, () => Array(len).fill(false));
    let maxLength = 0, start = 0;
    for(let i = len - 1; i >= 0; i--){
        for(let j = i; j < len; j++){
            if(s[i] === s[j] && (j - i <= 2 || dp[i + 1][j - 1])) {
                dp[i][j] = true;
                if(j - i + 1 > maxLength) {
                    maxLength = j - i + 1;
                    start = i;
                }
            }
        }
    }
    return s.substring(start, start + maxLength);
};

// Two Pointers
const longestPalindrome = function(s) {
    let maxLen = 0, start = 0;
    const expandFromCenter = (l, r) => {
        while (l >= 0 && r < s.length && s[l] === s[r]) {
            l--;
            r++;
        }
        return [l + 1, r - 1];
    };
    for (let i = 0; i < s.length; i++) {
        let [l1, r1] = expandFromCenter(i, i);
        if (r1 - l1 + 1 > maxLen) {
            maxLen = r1 - l1 + 1;
            start = l1;
        }
        let [l2, r2] = expandFromCenter(i, i + 1);
        if (r2 - l2 + 1 > maxLen) {
            maxLen = r2 - l2 + 1;
            start = l2;
        }
    }
    return s.slice(start, start + maxLen);
};

C:

Dynamic Programming:

// C implementation of the dynamic programming approach
bool **initDP(int strLen) {
    bool **dp = (bool **)malloc(sizeof(bool *) * strLen);
    for (int i = 0; i < strLen; i++) {
        dp[i] = (bool *)malloc(sizeof(bool) * strLen);
        for (int j = 0; j < strLen; j++) {
            dp[i][j] = false;
        }
    }
    return dp;
}

char * longestPalindrome(char * s){
    int strLen = strlen(s);
    bool **dp = initDP(strLen);
    int maxLength = 0, left = 0;

    for (int i = strLen - 1; i >= 0; i--) {
        for (int j = i; j < strLen; j++) {
            if (s[i] == s[j]) {
                if (j - i <= 1) {
                    dp[i][j] = true;
                } else if (dp[i + 1][j - 1]) {
                    dp[i][j] = true;
                }
            }
            if (dp[i][j] && j - i + 1 > maxLength) {
                maxLength = j - i + 1;
                left = i;
            }
        }
    }
    char *ret = (char*)malloc(sizeof(char) * (maxLength + 1));
    strncpy(ret, s + left, maxLength);
    ret[maxLength] = '\0';
    return ret;
}

Two Pointers:

// C implementation of the two pointers approach
int left, maxLength;

void extend(char *str, int i, int j, int size) {
    while (i >= 0 && j < size && str[i] == str[j]) {
        if (j - i + 1 > maxLength) {
            maxLength = j - i + 1;
            left = i;
        }
        j++;
        i--;
    }
}

char * longestPalindrome(char * s){
    left = maxLength = 0;
    int size = strlen(s);

    for (int i = 0; i < size; i++) {
        extend(s, i, i, size);
        extend(s, i, i + 1, size);
    }

    char *subStr = (char *)malloc(sizeof(char) * (maxLength + 1));
    strncpy(subStr, s + left, maxLength);
    subStr[maxLength] = '\0';

    return subStr;
}

C#:

Dynamic Programming:

public class Solution {
    
    public string LongestPalindrome(string s) {
        bool[,] dp = new bool[s.Length, s.Length];
        int maxLength = 0;
        int left = 0;
        int right = 0;
        for(int i = s.Length-1 ; i>=0; i--){
            for(int j = i; j <s.Length;j++){
                if(s[i] == s[j]){
                    if(j - i <= 1){ // Case 1 and Case 2
                        dp[i, j] = true;
                    }else if( dp[i+1, j-1] ){ // Case 3
                        dp[i, j] = true;
                    }
                }
                if(dp[i, j] && j-i+1 > maxLength){
                    maxLength = j-i+1;
                    left = i;
                    right = j;
                }
            }
        }
        return s.Substring(left, maxLength);
    }
}

Two Pointers:

public class Solution {
    int maxLength = 0;
    int left = 0;
    int right = 0;
    
    public string LongestPalindrome(string s) {
         int result = 0;
        for (int i = 0; i < s.Length; i++) {
            extend(s, i, i, s.Length); // Single character as center
            extend(s, i, i + 1, s.Length); // Two characters as center
        }
        return s.Substring(left, maxLength);
    }
    
    private void extend(string s, int i, int j, int n) {
        while (i >= 0 && j < n && s[i] == s[j]) {
            if (j - i + 1 > maxLength) {
                left = i;
                right = j;
                maxLength = j - i + 1;
            }
            i--;
            j++;
        }
    }
}