# Analysis of Time and Space Complexity in Recursive Algorithms!
Previously, in Let's Talk About the Time Complexity of Recursive Algorithms Through an Interview Question! (opens new window), we thoroughly explained the time complexity of recursive algorithms, but we didn't cover space complexity.
This article will deeply analyze the time and space complexity of recursive algorithms through examples such as calculating the Fibonacci sequence and binary search. Carefully reading through will broaden your understanding of recursion!
# Performance Analysis of Recursive Fibonacci Sequence Calculation
Let's first look at the recursive approach to calculating Fibonacci numbers.
int fibonacci(int i) {
if(i <= 0) return 0;
if(i == 1) return 1;
return fibonacci(i-1) + fibonacci(i-2);
}
2
3
4
5
Recursive algorithms are typically concise, and from a logical standpoint, the storage space required seems minimal, but the runtime memory requirement may not be so.
# Time Complexity Analysis
What is the time complexity of the recursive algorithm for computing Fibonacci numbers?
When discussing the time complexity of recursion, we noted that the time complexity of a recursive algorithm is essentially determined by: Recursive calls times * Time complexity per call.
From the above code, it's clear that each recursion involves O(1) operations. Let's examine how many times the recursion occurs, representing the recursive process when i is 5 as a tree:
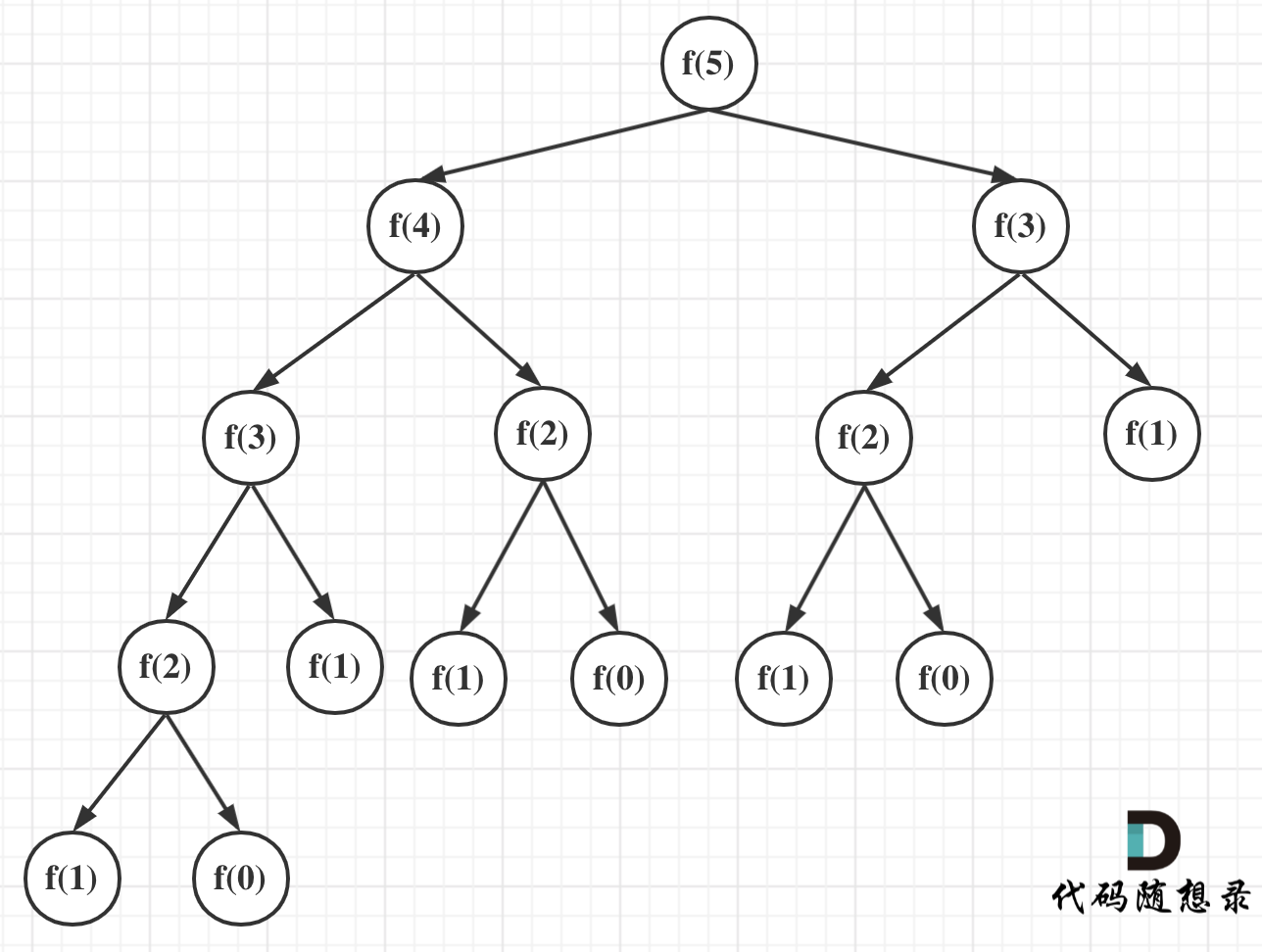
From the diagram, we can see that f(5) is the result of adding f(4) and f(3), and f(4) results from f(3) and f(2), and so on.
In this binary tree, each node represents a single recursion. So, how many nodes does this tree have?
We also mentioned earlier that a binary tree with depth k (where the root has depth 1) can have up to 2^k - 1 nodes.
Thus, the time complexity of this recursive algorithm is O(2^n), which is quite large. The amount of time required increases exponentially with larger n.
To illustrate this, let's conduct an experiment for a more intuitive understanding.
Below is C++ code to test for different n inputs and measure the time it takes to compute Fibonacci using this recursive code.
#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
int fibonacci(int i) {
if(i <= 0) return 0;
if(i == 1) return 1;
return fibonacci(i - 1) + fibonacci(i - 2);
}
void time_consumption() {
int n;
while (cin >> n) {
milliseconds start_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
fibonacci(n);
milliseconds end_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
cout << milliseconds(end_time).count() - milliseconds(start_time).count()
<<" ms"<< endl;
}
}
int main()
{
time_consumption();
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Based on this code, here are some experimental results:
Testing on a 2015 MacPro, CPU configuration: 2.7 GHz Dual-Core Intel Core i5
Test data:
- n = 40, time: 837 ms
- n = 50, time: 110306 ms
It is evident that the exponential time complexity O(2^n) is extremely large.
Thus, although this method of calculating Fibonacci numbers appears simple and clean, its time complexity is quite high, and it's generally not recommended to implement Fibonacci calculations this way.
The primary reason is the two recursive calls, which cause the time complexity to increase exponentially.
return fibonacci(i-1) + fibonacci(i-2);
Can we optimize this recursive algorithm? The key is to reduce the number of recursive calls.
Consider the following code:
// Version 2
int fibonacci(int first, int second, int n) {
if (n <= 0) {
return 0;
}
if (n < 3) {
return 1;
}
else if (n == 3) {
return first + second;
}
else {
return fibonacci(second, first + second, n - 1);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Here, we use first and second to record the two numbers to be added, thus only a single recursive call is needed.
Since each recursion decreases n by 1, there are n recursions, resulting in a time complexity of O(n).
Similarly, the recursion depth remains n, and the space required for each recursion is constant, so the space complexity remains O(n).
The complexity for the code (Version 2) is as follows:
- Time Complexity: O(n)
- Space Complexity: O(n)
Let's test the time consumption to verify:
#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
int fibonacci_3(int first, int second, int n) {
if (n <= 0) {
return 0;
}
if (n < 3) {
return 1;
}
else if (n == 3) {
return first + second;
}
else {
return fibonacci_3(second, first + second, n - 1);
}
}
void time_consumption() {
int n;
while (cin >> n) {
milliseconds start_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
fibonacci_3(1, 1, n);
milliseconds end_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
cout << milliseconds(end_time).count() - milliseconds(start_time).count()
<<" ms"<< endl;
}
}
int main()
{
time_consumption();
return 0;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
Test results:
- n = 40, time: 0 ms
- n = 50, time: 0 ms
The difference should be clear now!!
# Space Complexity Analysis
After discussing the time complexity of this recursive code, how do we determine its space complexity? Here's a formula for you: Space complexity of a recursive algorithm = Space complexity per recursion * Recursion depth
Why do we consider recursion depth?
Because the space required for each recursion is pushed onto the call stack (which is essentially a data structure used for memory management, analogous to stacks in algorithms), once a recursion ends, this stack pops out the data for that particular recursive call. Therefore, the maximum stack length is the recursion depth.
Now, let's analyze the space complexity of this recursion. As can be seen from the code, each recursion requires the same amount of space, so the space needed per recursion is a constant and does not change with n, resulting in a space complexity per recursion of O(1).
Let's examine the depth of the recursion:
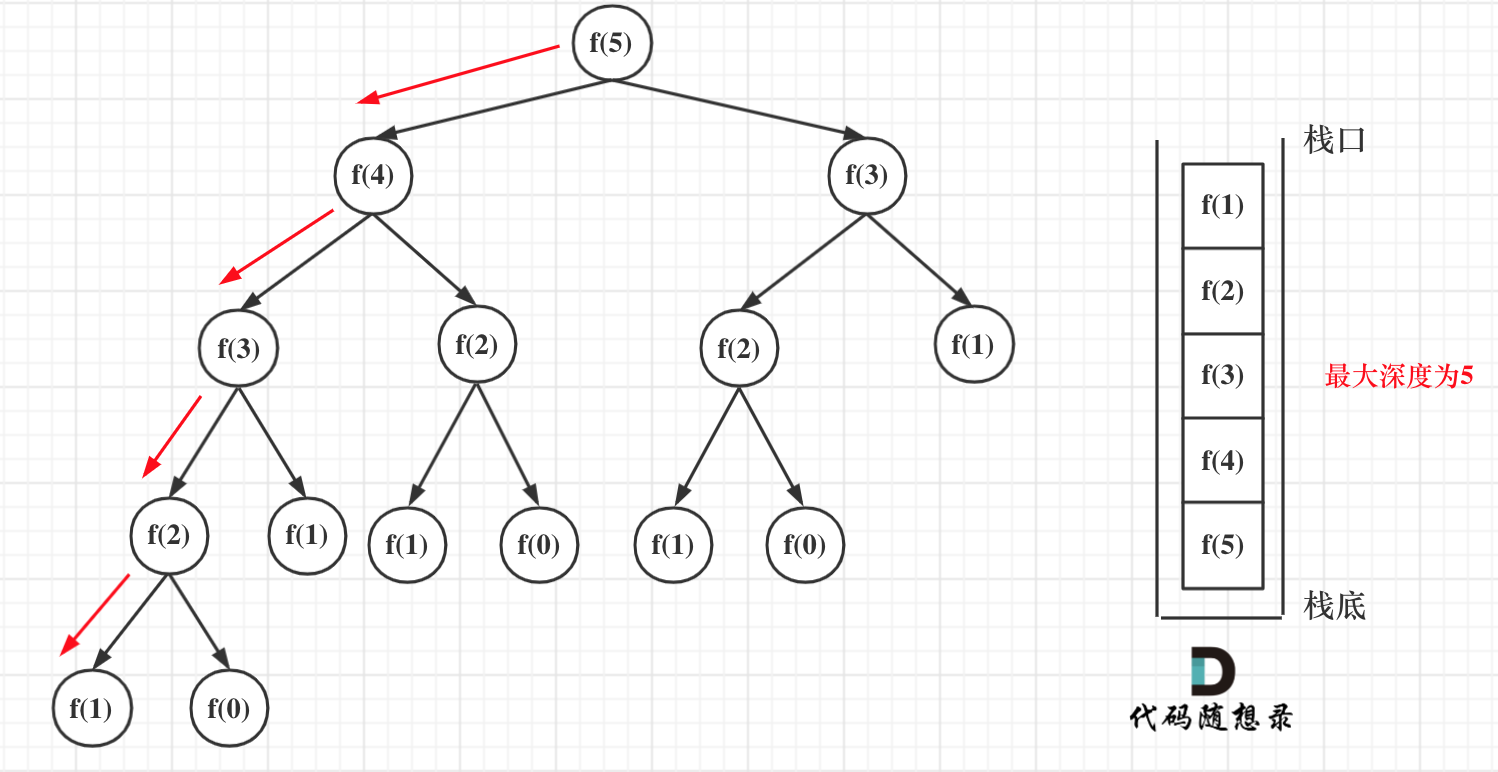
For the n-th Fibonacci recursion, the depth of the recursion call stack is n.
Thus, with the space complexity per recursion being O(1) and the recursion depth being n, the space complexity of this recursion code is O(n).
int fibonacci(int i) {
if(i <= 0) return 0;
if(i == 1) return 1;
return fibonacci(i-1) + fibonacci(i-2);
}
2
3
4
5
Finally, let's analyze the performance of different methods for calculating the Fibonacci sequence:
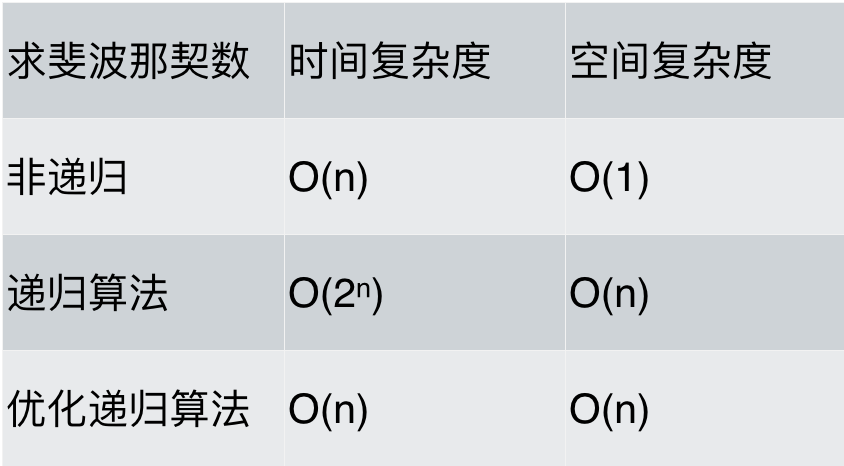
It is evident that when calculating Fibonacci numbers, recursive algorithms are not always the most optimal in terms of performance, although they do simplify the coding complexity.
# Performance Analysis of Binary Search (Recursive Implementation)
Let's take a look at a recursive implementation of the binary search algorithm.
int binary_search( int arr[], int l, int r, int x) {
if (r >= l) {
int mid = l + (r - l) / 2;
if (arr[mid] == x)
return mid;
if (arr[mid] > x)
return binary_search(arr, l, mid - 1, x);
return binary_search(arr, mid + 1, r, x);
}
return -1;
}
2
3
4
5
6
7
8
9
10
11
We know that the time complexity of binary search is O(logn). What about the space complexity of its recursive version?
Again, we look at Space complexity per recursion and recursion depth.
The space complexity per recursion mainly involves the arr array passed as a parameter. Note that in C/C++, when an array is passed as a function parameter, it’s not copied entirely but rather the address of the first element is passed.
This means each recursion shares the same memory space for the array, so the space complexity per recursion is a constant O(1).
Then, we consider the recursion depth. The recursion depth for binary search is logn, which is the length of the call stack, making the space complexity for this code equal to 1 * logn = O(logn).
It's important to note whether the language you use copies the entire value or just the address when passing function parameters. If it copies the entire value, then the space complexity of this binary search becomes O(nlogn).
# Summary
In this chapter, we thoroughly analyzed the space complexity of recursive implementations of Fibonacci and binary search, along with a discussion on time complexity.
There are stark differences between the time complexities of the two recursive methods for calculating the Fibonacci sequence, and our experiments confirmed that a time complexity of O(2^n) can be extremely time-consuming.
Through this article, readers should gain a deeper understanding of the time complexity and space complexity involved in recursive algorithms.
